Вопросы и задачи для самостоятельной работы
- Некоторые древние считали, что Ахиллес, бегущий со скоростью V за удаленной от него на расстояние L0 черепахи, уползающей от него со скоростью v < V, никогда ее не догонит из-за того, что за время его движения на отрезке пути L0 (и всех последующих отрезках до точки наблюдаемого им положения черепахи), последняя всегда будет удаляться на некоторое расстояние. Не пользуясь законом сложения скоростей или рассуждениями о дискретности пространства, приведите расчет, опровергающий приведенное ошибочное «рассуждение».
2. Не желающий оплачивать проезд в метро очень невоспитанный студент бежит вниз по эскалатору, идущему вверх, и насчитывает N 1 ступенек. На обратном пути он по привычке бежит вверх по эскалатору, идущему вниз и насчитывает N 2 ступенек. Сколько ступенек мальчик насчитает на неподвижном эскалаторе, если он хорошо тренируется и бегает вверх и вниз по эскалатору с одинаковой скоростью?
3. Спасатель сидит на пляже на расстоянии h 1 от воды и наблюдает, как на расстоянии h 2 от берега терпит бедствие его потенциальный клиент. Расстояние между перпендикулярами, опущенными на берег из точек нахождения спасателя и потенциального клиента – известно и равно L. По какой траектории должен двигаться спасатель для того, чтобы добраться до своего потенциального клиента за минимальное время? Скорости перемещения спасателя по пляжу и по воде - заданы и равны V1 и V2 ?
4. Честными ли являются соревнования пловцов на дистанциях одинаковой длины, проложенных по спокойной воде озера и по реке, если обе дистанции нужно поплыть в оба конца?
5. Сборщик фруктов идет со скоростью V 1 относительно ленты транспортера, движущегося со скоростью u. Получатель фруктов идет навстречу со скоростью V 2. С какой частотой получатель будет получать яблоки, если их кладут на ленту с частотой f 0?
Лекция 2
Кинематика: основные понятия
.
| Основными понятиями кинематики материальной точки являются ее радиус-вектор, скорость его изменения («вектор мгновенной скорости») и скорость измерения мгновенной скорости («вектор мгновенного ускорения»). Указанные кинематические величины связаны друг с другом через математические операции дифференцирования и взятие определенных интегралов, которые могут быть выполнены аналитически, графически или с помощью автоматизированных символьных вычислений на компьютере |
2.1. Перемещение. Средняя и мгновенная скорости
| Средняя скорость определяется как отношение перемещения к интервалу времени, за которое оно произошло. Мгновенная скорость (средняя скорость за малый промежуток времени) вычисляется как производная от радиус-вектора по времени. Перемещение вычисляется как определенный интеграл от мгновенной скорости по интервалу времени, н котором вычисляется перемещение. | ||||
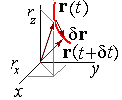
|
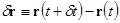
| (2.1) | Перемещение материальной точки за время d t. | |

| (2.2) | Средняя скорость. | ||

| (2.3) | Мгновенная скорость. | ||

|

| (2.4) | Определение мгновенной скорости по известной зависимости соответствующей координаты от времени. | |

| Рис. 2.1 Так можно находить производные функций, не умея дифференцировать, но имея на своем компьютере пакет «Математика». | |||
| 
| (2.5) | Определение координат материальной точки по известным зависимостям от времени проекций ее скоростей. | |

| Рис. 2.2 Так можно находить интегралы от многих функций, не умея дифференцировать, но имея на своем компьютере пакет «Математика». | |||

| (2.6) | Связь между координатой и мгновенной скоростью. | ||
2.2. Ускорение материальной точки
| Мгновенное ускорение связано с мгновенной скоростью абсолютно аналогично тому, как мгновенная скорость связана с радиус-вектором | |||
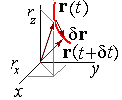
| 
| Рис.2.3 Радиус-вектор материальной точки и годограф вектора скорости. | |



| 

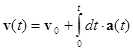
| (2.7) | Связь среднего и мгновенного ускорения с мгновенной скоростью. |
 
| (2.8) | Связь мгновенного ускорения с радиус-вектором. |
Пример. Движение тела по эллиптической траектории

| 
| 2.9) | Одна из возможных форм движения по эллиптической траектории. |

| 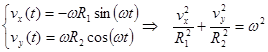
| (2.10) | Годограф скорости при движении по эллиптической траектории. |

| (2.11) | Ускорение при движении по эллиптической траектории. |
2.3. Равноускоренное движение
| В случае равноускоренного движения скорость оказывается линейной, а радиус-вектор функциями (векторными функциями) времени | ||

| (2.12) | Ускорение при равноускоренном движении остается постоянным. |

| (2.13) | При равноускоренном движении скорость является линейной функцией времени. |

| (2.14) | При равноускоренном движении координата является квадратичной функцией времени. |
Пример. Движение тела, брошенного под углом к горизонту

| 
| (2.15) | Начальные условия и конкретный вид ускорения |

| 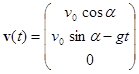
| (2.16) | Зависимость от времени компонент скорости тела, брошенного под углом к горизонту. |

| (2.17) | Зависимость координат тела от времени. | |

| (2.18) | Время подъема и максимальная высота подъема тела, брошенного под углом к горизонту и максима. | |

| (2.19) | Время и дальность полета тела, брошенного под углом к горизонту. | |

| (2.20) | Уравнение траектории тела, брошенного под углом к горизонту. |
2.4. Классический закон сложения скоростей и ускорений
| Вывод классических законов сложения скоростей и ускорения основаны на естественном для классической физики предположении об одинаковом течении времени в любых парах движущихся друг относительно друга системах отсчета. | |||

| 
| (2.21) | Связь между радиус-векторами, задающими положение материальной точки, в разных системах отсчета. |

| (2.22) | Классический закон сложения скоростей. | |

| (2.23) | Классический закон сложения ускорений. |
2.5. Преобразования Галилея
| Преобразование Галилея – частный случай классического закона сложения скоростей для двух систем отсчета, движущихся друг относительно друга вдоль осей «ох» с постоянной скоростью | |||

| 
| (2.21) | Преобразования Галилея. |
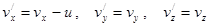
| (2.22) | Классический закон сложения скоростей. |
Вопросы и задачи для самостоятельной работы
1. Машинист покоящегося электровоза с неудовольствием видит, что на расстоянии L от него находится вагон, приближающийся к локомотиву равнозамедленно (скорость V, ускорение a < 0). С каким постоянным ускорением должен начать двигаться электровоз для того, чтобы между ним и вагоном произошла мягкая сцепка?
2. К месту ДТП с двух равноудаленных от него стоянок одновременно выезжает дорожный патруль и скорая помощь. Автомобиль полиции первую треть пути движется равноускоренно, после достижения максимально допустимой скорости V вторую треть пути равномерно и, наконец, последний участок – равнозамедленно. Карета скорой помощи развивает ту же максимальную скорость V, но движетсяравноускоренно, равномерно и равнозамедленно на равных интервалах времени движения. Какая из служб прибудет к месту ДТП раньше?
3. Найти зависимости от времени скорости и радиус-вектора материальной точки, начинающей двигаться из начала координат с направленным вертикально вниз ускорением g 0 и постоянной «тряской» Q (скоростью изменения ускорения), направленной а) горизонтально, б) вертикально вверх.
4. На одном из островов Бермудского треугольника ускорение свободного падения наклонено в северном направлении под углом α к вертикали. Туземец стреляет из лука с начальной скоростью V0 по углом β к поверхности острова. На каком расстоянии от туземца упадет стрела, если он с трелял а) га юг, б) на север, в) на запад?
5. Микроавтомобиль подъезжает к прямоугольной выбоине на дороге, размеры которой H * L много больше размеров автомобиля. Все удары автомобиля о стенки выбоины абсолютно упругие. При какой начальной скорости автомобиля он покинет выбоину и продолжит движение в исходном направлении. Найти все решения.
6. Небольшой шарик отпускают без начальной скорости с высоты H над наклонной плоскостью, составляющей угол α c горизонтом. Все отскоки шарика от плоскости абсолютно упругие. Найти расстояние между первым и 2018-м ударом.
7. Винни-Пух неподвижно висит на воздушном шарике на высоте H над поверхностью Земли, точно под ним располагается Кролик. На расстоянии L от места вероятного падения медвежонка расположен Пятачок в пневматической пушкой. В момент выстрела Винни-Пух отпускает нитку шара и начинает свободно падать. Под каким углом и с какой скоростью Пятачок должен выпустить ядро из пушки для того, чтобы упавший медведь не раздавил Кролика?
Лекция 3
Кинематика криволинейного движения
| Для описания криволинейного движения удобно ввести векторы угла поворота, угловой скорости и ускорения, связанные друг с другом аналогично тому, как связаны радиус-вектор, скорость и ускорение |
3.1. Скалярное произведение. Базис
| Скалярное произведение – математическая операция, ставящая в соответствие любой паре векторов число. Введение скалярного произведения позволяет определить понятия взаимной ортогональности и ортонормированного базиса. | |||

|

| (3.1) | Определение скалярного произведения. |

|

| (3.2) | Линейность скалярного произведения по его сомножителям. |

| (3.3) | Свойство векторов ортонормированного базиса. | |

| (3.4) | Вычисление скалярного произведения через координаты сектора. | |
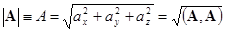
| (3.5) | Длина вектора |
3.2. Путь, проходимый материальной точкой
| Пройденный точечным телом путь в отличие от вектора перемещения является скалярной величиной, равной длине отрезка криволинейной траектории тела. | |||

|

| (3.6) | Математическое определение длины отрезка кривой. |
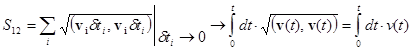
| (3.7) | Вычисление длины отрезка траектории по известной скорости. |
Пример. Путь, пройденный телом, брошенным под углом к горизонту

| (3.8) | Вычисление модуля вектора скорости. |

| (3.9) | Вычисление интеграла при помощи пакета «Математика». |

| (3.10) | Длина траектории тела, брошенного под углом к горизонту. |
3.3. Векторное произведение
| Векторное произведение двух векторов может быть введено в трехмерном пространстве, как антикоммутативная операция, ставящая в соответствие двум сомножителям псевдовектор | |||

|

| (3.11) | Определение векторного произведения. |

|
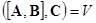

| (3.12) | Смешанное скалярно-векторное произведение и его основное свойство. |


| (3.13) | Свойство линейности векторного произведения по его сомножителям и идея доказательства этого свойства. | |

| (3.14) | Вычисление векторного произведения по декартовым координатам перемножаемых векторов. | |

| (3.15) | Правило «bac-cab» и идея его доказательства. |
3.4. Угловая скорость и угловое ускорение
| Переход к описанию угла поворота, угловой скорости и углового ускорения с помощью псевдовекторов позволяет легко получить связь между линейными скоростью и ускорением и их угловыми аналогами. | |||

| 


| (3.16) | Определение угловой скорости. |

|

| (3.17) | Связь угловой и линейной скорости. |

| (3.18) | Угловое ускорение. | |

| (3.19) | Связь линейного и углового ускорений. |
Пример. Движение тела по дуге окружности

| (3.20) | Движение по окружности с постоянной угловой скоростью. |

| (3.21) | Описание равномерного вращения по окружности в декартовых координатах. |

| (3.22) | Нормальное (центростремительное) ускорение при равномерном вращении по окружности. |

| (3.23) | Равноускоренное движение по окружности. |
3.5. Нормальное и тангенциальное ускорения
| В случае криволинейного движения вектор ускорения может быть разложен на нормальную и тангенциальную составляющие, непосредственно связанный с кривизной траектории и скоростью изменения величины (модуля) линейной скорости соответственно | |||

| 
| (3.24) | Разложение ускорения на нормальное и тангенциальное. |
Пример. Движение тела, брошенного под углом к горизонту: нормальное и тангенциальное ускорения

| (3.25) | Нормальное и тангенциальное ускорения тела, брошенного под углом к горизонту. |
Вопросы и задачи для самостоятельной работы
1. Первоначально покоившаяся материальная точка начинает двигаться по окружности радиусом R с постоянным угловым ускорением. Получить явные зависимости от времени декартовых координат и проекций линейной скорости и ускорения (r x(t), v x(t), a x(t), x = x, y). Убедитесь непосредственным сравнением в справедливости соотношений (3.21) для рассмотренного случая.
2. Найти радиус кривизны траектории тела, брошенного под углом к горизонту в каждой точке его траектории.
3. Карусели, вращающиеся с угловой скоростью ω, начинают арвномерно тормозиться и останавливаются, сделав N оборотов. Сколько времени длилось торможение?
4. Эллипс имеет полуоси a и b. Чему равен максимальный и минимальный радиусы кривизны кривой, ограничивающей эллипс. Указание – воспользоваться решениями задач на расчет скорости и ускорения материальной точки, вращающейся по эллипсу с постоянной угловой скоростью.
5. Покоившееся тело начинает двигаться по окружности радиусом R с постоянным угловым ускорением β. Какова будет величина (модуль) линейного ускорения тела через время Т после начала движения?
Лекция 4
Основы динамики материальной точки
| Основу классической динамики материальной точки составляет совокупность трех законов Ньютона. Эти законы по существу дают рецепт вычисления ускорений очечных тел, что в свою очередь открывает возможность нахождения их скоростей и радиус-векторов, т.е. решения основной задачи механики |
4.1. Законы Ньютона
| Первый закон Ньютона постулирует существование инерциальных систем отсчета, т.е. систем, в которых свободные тела движутся без ускорений. Второй закон представляет собой описание экспериментально наблюдаемого в инерциальных системах отсчета факта пропорциональности ускорения тела действующей на него силе, определяемой через процедуру измерения с помощью специального прибора - динамометра. Следствием второго закона является независимость от механического состояния тел их инертной массы, вводимой как коэффициент пропорциональности между силой и ускорением. Третий закон Ньютона описывает экспериментальный факт равенства по величина и противоположность по направлению возникающих при парных взаимодействиях сил, действующих на взаимодействующие тела. | |||

|

| (4.1) | Первый закон Ньютона: существуют инерциальные системы отсчета (т.е. такие системы, в которых свободные тела движется без ускорений). |

| (4.2) | Второй закон Ньютона (ускорение тела пропорционально приложенной к нему силе) и определение массы. | |
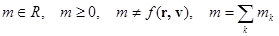
| (4.3) | Свойства массы, постулируемые в классической механике. | |
|
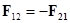

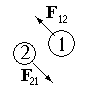
| (4.4) | Третий закон Ньютона: при взаимодействии двух тел всегда возникают силы, приложенные к каждому из них, равные по величине и противоположно направленные. |
4.2. Импульсная формулировка второго закона Ньютона
| Импульсная формулировка второго закона Ньютона выводится из классической в случае неизменности инертной массы тела, но носит более общий характер и оказывается применимой в случае движения тела с переменной массой | ||

| (4.5) | Определение импульса материальной точки. |

| (4.6) | Скорость изменения импульса. |

| (4.7) | Импульсная формулировка второго закона Ньютона. |

| (4.8) | Второй закон Ньютона в случае движения тела с переменной массой. |
4.3. Второй закон Ньютона как уравнение движения
| С точки зрения математики второй закон Ньютона представляет собой обыкновенное дифференциальное уравнение второго порядка с постоянными коэффициентами, для однозначного решения которого необходимо задание двух начальных условий (для радиус-вектора и скорости тела). В результате поведение макроскопических систем в классической физике оказывается принципиально рассчитываем и, следовательно, детерминированным. | ||

| (4.9) | Упрощенная схема решения основной и обратной задачи механики. |

| (4.10) | Второй закон Ньютона как уравнение движения (дифференциальное уравнение второго порядка в обыкновенных производных). |
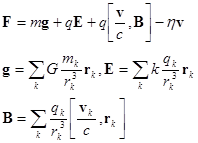
| (4.11) | Основные силы, рассматриваемые в классической физике (использована система единиц Гаусса). |
4.4. Прямая задача механики
| Прямая задача механики (определение действующих на тело сил по его движению всегда имеет однозначное решение и по сути сводится к вычислению второй производной от радиус вектора, изменяющегося во времени по известному закону | ||

| (4.12) | Решение прямой задачи механики. |
Пример. Суперпозиция гармонических колебаний одинаковой частоты

| (4.13) | Движение, представляющее собой суперпозицию гармонических колебаний вдоль каждой из координат, происходит под действием силы, линейной по смещению. |
4.5. Обратная задача механики (случай явной зависимости силы от времени)
| Обратная задача механики (расчет движения тела по известной действующей на него силе легко решается в случае известной явной зависимости от времени силы, действующей на рассматриваемое тело при заданных начальных условиях легко решается в результате вычисления двух определенных интегралов (от ускорения и от найденной скорости). | ||

| (4.14) | Решение основной задачи механики в случае силы, явно зависящей от времени, и только от него. |
Пример. Электрон во внешнем электрическом поле, изменяющемся во времени по гармоническому закону

| 
| (4.15) | Сила, действующая на электрический заряд, помещенный в конденсатор, на обкладки которого подано переменное напряжение. |
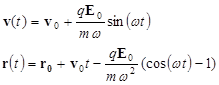
| (4.16) | Движение электрического заряда в пространственно однородном электростатическом поле, изменяющемся во времени по гармоническому закону. |
Вопросы и задачи для самостоятельной работы
1. Однажды Лебедь, Рак и Щука решили сдвинуть с места воз массой M, покоившийся на очень скользкой горизонтальной поверхности. Все персонажи воздействовали на воз си силами, лежащими в одной плоскости. Лебедь тащил воз на север и вверх с силой F Л, действующей под углом α к горизонтали. Щука – на север и вниз с силой F Щ , действующей под углом β к горизонтали. Рак был способен лишь к воздействию на воз в горизонтальном направлении. С какой силой рак должен тащить воз для того, чтобы реализовалась ситуации, описанная в известном произведении Крылова?
2. Рассмотреть движение электрона в плоском конденсаторе емкости C, первоначально заряженном до напряжения U 0 и разряжающемся через сопротивление R. Первоначально электрон покоился в начале координат.
3. Как будет изменяться во времени скорость вертолета, неподвижно в висевшего на высоте H над поверхностью Земли, если сила вертикальной тяги его двигателя изменяется во времени по закону
 ?
?
При каких условиях вертолет не ударится о поверхность Земли?
4. Покоящийся на горизонтальной поверхности (коэффициент трения µ) груз массой m пытаются сдвинуть с места, действуя на него силой, приложенной под углом α к горизонту. С какой минимальной силой нужно действовать на груз для того, чтобы он пришел в движение?
5. Внутри железнодорожного вагона, движущегося со скоростью v, помещен привязанный к полу невесомой нитью наполненный гелием шарик, Нить составляет угол α с вертикалью. Чему равен радиус закругления железнодорожных путей, если они расположены строго горизонтально?
6. Поворот шоссе радиусом R оформлен в виде трека с углом наклона дороги α в сторону поворота. С какой скоростью может автомобиль проходить поворот для того, чтобы не возникло проскальзывания? Коэффициент трения колес о дорогу равен µ.
7. Очень Невоспитанный Мальчик посадил Очень Хорошую Девочку в бочку радиусом R и раскрутил ее до такой угловой скорости ω, что девочку прижало к стенке бочки столь сильно, что после выпадения дна «аттракциона» она осталась неподвижной относительно его стенки. Мальчик начал равномерно замедлять вращение бочки так, что она остановилась, совершив N полных оборотов. Через какое время Т после начала торможения девочка начнет проскальзывать относительно стенки бочки?
8. Через идеальный невесомый блок перекинута невесомая нерастяжимая нить, к концам которой подвешены два груза массами m 1 и m 2, расстояние между которыми по вертикали равно Н (груз m 2 расположен выше). Над вторым грузом на нити сидит обезьяна массой М, запрограммированная так перебирать лапами, чтобы всегда оставаться на месте. Первоначально покоившуюся систему отпускают. Через какое время грузы окажутся на одной высоте?
Лекция 5
Одномерное движение под действием сил, зависящих от положения и скорости тела, в простейших случаях
| Простые задачи классической механики – удобный повод познакомиться со стандартными методами решения обыкновенных дифференциальных уравнений и приобрести опыт анализа характерных типов движений под действием различных сил |
5.1. Сила,, зависящая только от скорости и сонаправленная с ней
| При движении тел под действием сил вязкого трения характерно экспоненциальное убывание их скорости, обеспечивающее конечность тормозного пути при бесконечно большом времени торможения. | ||

| (5.1) | Общий вид силы, зависящей от скорости и направленной вдоль ее направления. |

| (5.2) | Решение задачи о движении тела под действием силы (5.1). |
Пример. Движение тела под действием сил вязкого трения

| (5.3) | Сила вязкого трения. |

| (5.4) | Уравнение движения и начальное условие. |

| (5.5) | Решение задачи (5.4) методом (5.2). |
5.2 Падение тела в вязкой среде
| При падении покоившихся тел в вязкой среде по мере их разгона постепенно возрастает роль сил трения, что приводит к постепенному переходу от первоначально равноускоренного движения к равномерному | |||
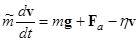
| (5.6) | Уравнение движения тела, падающего в вязкой среде. В левую часть уравнения включена присоединенная масса. | |

| 
| (5.7) | Проекция уравнения движения (5.6) на вертикальную ось. |

| (5.8) | Решение дифференциального уравнения (5.7). | |

| (5.9) | Определение константы интегрирования по начальному условию. | |

| 
| (5.10) | Построение графика зависимости v(t). |

| (5.11) | Зависимость от времени координаты тела, падающего в вязкой среде. |
5.3. Одномерное движение частицы под действием силы, зависящей от координаты
| При решении уравнения движения под действием сил, зависящих только от пространственного положения тела, естественным образом возникает закон сохранения механической энергии | ||
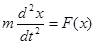
| (5.12) | Уравнение одномерного движения частицы в поле потенциальных сил. |

| (5.13) | Первый интеграл движения. |

| (5.14) | «Закон сохранения механической энергии» — результат интегрирования уравнения (15.13). |
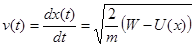
| (5.15) | Связь скорости с координатой в случае одномерного движения в поле потенциальных сил. |

| (5.16) | Искомая связь координаты тела и времени движения. |
Движение, описываемое линейным дифференциальным уравнением с постоянными коэффициентами
| Характер движения линейного осциллятора с вязким трением существенно зависит от величины диссипативной силы: при увеличении коэффициента вязкого трения возрастает характерная скорость затухания колебаний, возрастает их период, а при превышении коэффициентом вязкого трения критического значения происходит переход к апериодическому движению маятника. | |||

| 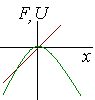
| (5.21) | Уравнение движения вблизи точки неустойчивого равновесия и стандартные обозначения для записи уравнения второго порядка. |

| (5.22) | Вид пробного решения уравнения (5.21) и характеристическое уравнение для l. | |

| (5.23) | Два линейно независимых решения уравнения (5.22). | |

| (5.24) | Общее решение уравнения (5.22) и конкретное решение в случае тела, выпущенного из точки неустойчивого равновесия с заданной начальной скоростью. | |

| (5.25) | Уравнение движения осциллятора с затуханием вблизи точки устойчивого равновесия | |

| (5.26) | Апериодический режим движения осциллятора с затуханием (реализуется в случае больших коэффициентов вязкого трения). | |

| (5.27) | Апериодический режим движения осциллятора с затуханием (реализуется в случае малых коэффициентов вязкого трения). | |

| (5.28) | Критический режим осциллятора |
5.5. Движение, описываемое нелинейным дифференциальным уравнением
(реальный маятник)
| При решении задач на расчет движения систем, описываемых нелинейными уравнениями, как правило приходится использовать численное интегрирование уравнения движения. | |||

| 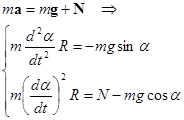
| (5.29) | Уравнение движения реального маятника. |

| (5.30) | Уравнение в стандартных обозначениях. | |

| Рис. 5.3. При малых начальных скоростях колебания оказываются близкими к гармоническим, поскольку входящий в уравнение движения синус может быть аппроксимирован линейной функцией, что приводит к уравнению, тождественному уравнению гармонических колебаний (5.17). | ||

| Рис. 5.4. При приближении начальной скорости к критическому значению, соответствующему энергии перехода системы в состояние неустойчивого равновесия, колебания начинают резко отличаться от гармонических: в области изменения направления движения (поворота) тело проводит аномально большое время. | ||
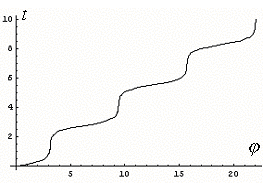
| Рис. 5.5. При превышении начальной скоростью критического значения колебательный режим принципиально меняется: маятник начинает вокруг точки подвеса с угловой скоростью, сильно зависящей от положения груза. | ||

| Рис. 5.6. При больших начальных скоростях незначительные изменения скорости, вызванные действием на маятник силы тяжести, становятся малосущественными. |
Вопросы и задачи для самостоятельной работы
1. Решить задачу о зависимости от времени координаты тела, движущегося пол действием силы вязкого трения, величина которой зависит от скорости по квадратичному закону: