| Движение твердого тела можно рассматривать как совокупность поступательного движения его центра масс и вращения вокруг этой точки, | |||

|

| (12.9) | Поступательное движение. |

|

| 12.10) | Вращательное движение вокруг фиксированной оси. |

|

| (12.11) | Плоское движение, при котором каждая точка движется по плоской кривой, может быть представлено как вращение твердого тела вокруг оси, перемещающейся в пространстве. |

|

| (12.12) | Неоднозначность разложения плоского движения на вращательное и поступательное: для каждой выбранной точки тела может быть введен полюс так, что перемещение этой точки представимо как результат поворота вокруг этого полюса. |
12.5. Произвольное движение твердого тела. Теорема Эйлера
| По т.Эйлера скорость произвольной точки твердого тела можно найти как векторную сумму скорости движения его центра масс и скорости вращательного движения вокруг этого центра | ||

| (12.13) | Теорема Эйлера. |
Вопросы и задачи для самостоятельной работы
- Однородная балка массой M и длиной L лежит на краю пропасти так, что четвертая часть ее длины не имеет опоры. Мальчик массой m начинает идти по балке в стороны обрыва с постоянной скоростью v. Через какое время после начала движения мальчик окажется в состоянии невесомости?
- Лестница длиной L и массой m стоит на полу, опираясь на стену, составляя заданный угол a с вертикалью. На какую высоту может подняться человек массой M по этой лестнице, если коэффициент трения лестницы о пол и стеру одинаков и равен m?
- Центром тяжести называется точка приложения равнодействующей гравитационных сил, действующих на тело, расположенное вблизи поверхности Земли. Показать, что в случае тел небольших размеров (по сравнению с размерами Земли) положения центра тяжести и центра масс абсолютно твердого тела совпадают.
- Мост строится из одинаковых прочных балок длиной L, но без каких-либо болтов или раствора, соединяющего балки друг с другом. Каждая следующая балка подводится под конструкцию так, чтобы она не опрокидывалась под собственным весом. Какой длины мост может быть построен по описанному алгоритму?
Лекция 13
Абсолютно твердое тело. Динамика
| При описании поступательного движения центра масс твердого тела и его вращательного движения прослеживается тесные аналогии между уравнениями, связывающими характеристики поступательного движения, и уравненямимя для аналогичных характеристик вращения твердого тела. |
13.1. Момент импульса твердого тела, тензор инерции
| Подобно тому, как масса тела может рассматриваться как коэффициент пропорциональности между скоростью его центра масс и его полным импульсом, может быть введен момент инерции как коэффициент пропорциональности между моментом импульса и угловой скоростью. Принципиальным отличием является то, что масса является скаляром, а момент инерции тензорной величиной, т.е. описывается с помощью симметричной относительно диагонали матрицы (таблицы из 9 чисел). | ||

| (13.1) | Момент импульса твердого тела в случае произвольно расположенного полюса. |

| (13.2) | Момент импульса твердого тела относительно полюса, расположенного либо в центре масс, либо в точке неподвижной оси. |

| (13.3) | Тензорный характер связи между моментом импульса и угловой скоростью. |

| (13.4) | Связь между моментом импульса и частотой вращения в координатном представлении. |

| (13.5) | Способ вычисления компонент тензора инерции твердого тела. |

| (13.6) | Тензор инерции твердого тела. |

| (13.7) | Возможность приведения матрицы тензора инерции к диагональному виду (приведение к осям свободного вращения). |

| (13.8) | Связь между моментом импульса и частотой в системе координат, связанной с осями свободного вращения. |
Пример. Момент инерции тонкого стержня

|

| (13.9) | Определение тонкого однородного стержня. |

| (13.10) | Равенство нулю недиагональных элементов матрицы тензора момента инерции стержня, вычисляемого в выбранной системе координат. | |

| (13.11) | Вычисление диагональных элементов матрицы тензора момента инерции цилиндра, вычисляемого в выбранной системе координат. | |

| (13.12) | Момент инерции однородного цилиндра радиуса R высотой H=2l. | |

| (13.13) | Момент инерции тонкого однородного стержня (ротатора). |
13.2. Кинетическая энергия
| Кинетическая энергия твердого тела представима суммой кинетических энергий движения его центра масс и вращения | ||

| (13.14) | Кинетическая энергия твердого тела. |

| (13.15) | Выражение кинетической энергии твердого тела через скорость полюса, угловую скорость вращения, импульс и момент импульса твердого тела. |

| (13.16) | Кинетическая энергия твердого тела с закрепленной осью вращения. |

| (13.17) | Кинетическая энергия в случае полюса, помещенного в центр масс твердого тела. |

| (13.18) | Выражение для кинетической энергии через скорость центра масс и угловую скорость вращения твердого тела. |
13.3. Вращение твердого тела вокруг закрепленной оси
| В случае вращения твердого тела вокруг закрепленной оси момент инерции относительно нее оказывается скалярной величиной. В результате уравнения, описывающие вращательное движение с точностью до переобозначений (замены линейных величин на угловые) совпадают с их аналогами для поступательного движения материальной точки. | |||

|

| (13.19) | Приращение вектора, обусловленное поворотом на малый угол dj. |

|

| (13.20) | Центростремительная сила и момент сил, действующие на твердое тело со стороны оси, закрепленной в подшипниках. |

| (13.21) | Связь между угловым ускорением и моментом внешних сил, приложенных к телу, имеющему закрепленную ось. | |

| (13.22) | Другой способ получения соотношения (3.21). | |

| (13.23) | Условие свободного вращения без закрепленной оси: оси свободного вращения совпадают с осями системы координат, в которой матрица тензора инерции диагонализуется |
13.4. Свободное вращение твердого тела
| Свободное сращение твердого тела возможно лишь вокруг трех взаимно перпендикулярных осей («осей свободного вращения»), для которых матрица момента инерции имеет диагональный вид | ||||

|

| (13.23) | Симметричный волчок. | |

| 
| (13.24) | Связь между угловой скоростью и сохраняющимся во времени моментом импульса. | |

|

| (13.25) | Вычисление угловой скорости прецессии симметричного волчка. | |

| (13.26) | Скорость вращения волчка вокруг оси симметрии. | ||
13.5. Вращающееся тела под воздействие внешних сил
| Движение тел с вращающимися частями («гироскопов») нередко обладает рядом особенностей, иногда весьма неожиданных с позиций «здравого смысла», базирующегося на наблюдениях за движением тел без вращающихся элементов | ||||

|

| (13.27) | Прецессия гироскопа с несимметричным подвесом, испытывающим нескомпенсированный момент сил тяжести и реакции опоры. | |

| 
| (13.28) | Прецессия симметричного волчка. | |
Вопросы и задачи для самостоятельной работы
1. Вычислить моменты инерции следующих геометрических примитивов (геометрические размеры заданы, полюс помещен в центр масс), считая, что масса равномерно распределена по объему: а) тонкий сферический слой, б) шар, в) прямоугольный параллелепипед, г) круговой конус.
2. По наклонной плоскости, составляющей угол a с горизонтом, с высоты H без начальной скорости начинает скатываться а) шар, б) цилиндр радиуса R, массой M. Определить скорости каждого из тел в конце наклонного участки, если известно, что они катятся без проскальзывания.
3. Показать, что незакрепленный куб может совершать свободное устойчивое вращение вокруг любой оси, проходящей через его центр. Найти энергия вращения, если заданы масса куба, длина его ребра и угловая скорость.
Лекция 14
Релятивистская кинематика
| Основания специальной теорией относительности, первоначально создававшейся как расширение классической механики в область электромагнитных явлений, описываемых уравнениями Максвелла, могут быть обоснованы с использованием постулатов Эйнштейна, успешно прошедших тщательную и многоплановую экспериментальную проверку. |
14.1. Необходимость перехода к релятивистскому описанию
| Основанная на преобразованиях Галилея классическая механика приходит в противоречия с ядом выводов магнитостатики и электродинамики Максвелла. | ||

| (14.1) | Инвариантность основного закона классической механики относительно преобразований Галилея в случае сил, зависящих только от относительного положения тел. |

| (14.2) | Возможность нарушения инвариантности второго закона Ньютона относительно преобразований Галилея в случае учета магнитных взаимодействий. |

| (14.3) | Преобразования Галилея, сохраняющие инвариантность уравнений классической динамики и преобразования Лоренца, обеспечивающие инвариантность уравнений электродинамики Максвелла. |
14.2. Постулаты СТО. Синхронизация часов. Измерение расстояний.
Относительность одновременности
| Положенные в основу СТО постулаты Эйнштейна являются обобщением идей, принятых в классической механике. Несколько неожиданным следствием из них являются выводы об относительном (т.е. зависящем от состояния наблюдателя) характере некоторых физических утверждений, ранее казавшихся абсолютными | |||

|

| (14.4) | Алгоритм синхронизации часов при помощи светового импульса. |

|

| (14.5) | Алгоритм измерения расстояний. |

| Рис. 14.1 Относительность одновременности: световой импульс, испущенный из середины отрезка, движущегося вместе с системой К’, доходит одновременно до его концов. В неподвижной системе отсчета указанные события происходят не одновременно. |
14.3. Релятивистские эффекты замедления времени и сокращения длин отрезков
| Постулаты СТО совместно с рядом разумных допущений о свойствах симметрии позволяют обосновать известные релятивистские эффекты замедления времени и сокращения длин движущихся отрезков, ориентированных вдоль вектора скорости относительного движения систем отсчета. | ||||
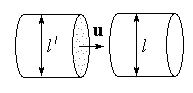
| Рис. 14.2 К доказательству свойства инвариантности длин отрезков, ориентированных перпендикулярно скорости их движения. | |||

| Рис.14.3. Траектории светового импульса в световых часах, расположенных в неподвижной и движущейся системе отсчета с точки зрения неподвижного наблюдателя. | |||

| (14.6) | Релятивистский эффект преобразования увеличения интервалов времени (замедления времени) в движущихся системах отсчета. | ||

| 
| (14.7) | Релятивистский эффект сокращения длин отрезков, направленных вдоль скорости относительного движения наблюдателя. | |

| 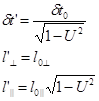 
| (14.8) | Сводка формул, преобразования длин отрезков и интервалов времени при переходе в движущуюся систему отсчета. U — скорость системы отсчета, выраженная в единицах с. | |
14.4. Преобразования Лоренца
| Преобразования Лоренца, первоначально предложенные как обобщение преобразований Галилея, сохраняющее инвариантность уравнений электродинамики, могут быть получены из релятивистских законом замедления времени и изменения длин отрезков, являющихся следствием постулатов Эйнштейна. | |||

| 
| (14.9) | Преобразование координат при переходе к движущейся системе отсчета. |
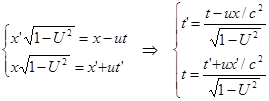
| (14.10) | Преобразования Лоренца для времени как следствие уравнений (14.9). | |

| (14.11) | Определение скорости с учетом различия хода времени в различных системах отсчета. | |

| (14.12) | Релятивистский закон сложения скоростей. |
Пример. Аберрации звездного неба

|

| (14.13) | Вектор скорости света, приходящего от звезды, находящейся в зените, с точки зрения наблюдателя, находящегося в гелиоцентрической системе отсчета. | |

| 
| (14.14) | Изменение наблюдаемого положения звезды, вызванное орбитальным движением Земли. | |
14.5. Четырехмерное пространство-время
| Удобной и наглядной геометрической интерпретацией преобразований Лоренца является четырехмерное пространство-время, особенности геометрических свойств которого отличаются от привычно постулируемых аксиом евклидовой геометрии | |||

| 
| (14.15) | Преобразование координат вектора в результате поворота системы координат вокруг оси z на угол j. |

| (14.16) | Матрица преобразования координат вектора при повороте системы координат. | |
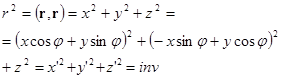
| (14.17) | Инвариантность квадрата трехмерного вектора относительно поворота системы координат вокруг одной из координатных осей. | |

| (14.18) | Произвольный поворот в трехмерном пространстве, определяемый углами Эйлера. | |

| (14.19) | Нарушение инвариантности квадрата длины вектора при переходе в движущуюся систему отсчета. | |

| (14.20) | Инвариантная относительно преобразований Лоренца комбинация компонент четырехвектора. | |
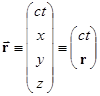
| 
| (14.21) | Описание события при помощи четырехаектора в пространстве Минковского. |

|

| (14.22) «Физический смысл» время- подобного интервала между двумя точками, лежащими на мировой линии равномерно движущейся частицы – время движения частицы между двумя точками пространства, измеренное по ее часам. | |

| 
| (14.23) | «Поворот» в пространстве Минковского, соответствующий переходу в движущуюся систему отсчета и иллюстрация относительности одновременности событий. |

| (14.24) | Построение простейшего инварианта из компонент четырехвектора. | |

| (14.25) | Метрический тензор четырехмерного псевдоевклидова пространства-времени Минковского. | |

| (14.26) | Скалярное произведение двух четырех векторов |
Пример. Парадокс близнецов

| 
| (14.27) | Связь интервалов времени, проведенных по часам неподвижного наблюдателя и «путешественника». |
Вопросы и задачи для самостоятельной работы
- Приводит ли к нарушению инвариантности относительно преобразования Галилея учет сил вязкого трения, которые, как известно, зависят от скорости тела?
- Время жизни покоящегося p-мезона составляет t=2.5×10-8 с. На какое расстояние успеет отлететь частицы от ускорителя, если она вылетает из него с ультрарелятивистской скоростью v/c-1=5×10-5? Постарайтесь решить задачу как в системе отсчета, связанной с ускорителем, так и в системе, связанной с летящей частицей.
- Найдите матрицу, осуществляющую преобразования координат вектора при повороте системы координат на углы Эйлера.
- Найдите матрицу, осуществляющую преобразования координат вектора при «четырехмерном повороте», соответствующем переходу из неподвижной системы отсчета, в инерциальную систему, движущуюся с заданной скоростью относительно первой.
- Покажите, что построенное в соответствии с (14.24) скалярное произведение двух четырехвекторов, компоненты которых преобразуются в соответствии с преобразованиями Лоренца, является релятивистским инвариантом.
- Непосредственной подстановкой преобразований Лоренца покажите, что «четырехскалярное произведение» не изменяется при переходе от одой инерциальной системы отсчета к лругой
Лекция 15
Релятивистская динамика
| Релятивистская динамика с троится как четырехмерный аналог классической механики с учетом требования написания уравнений, включающих в себя только четырехвектоы (совокупности из четырех величин, преобразующихся при поворотах как их трехмерные аналоги, а при переходе в движущиеся системы отсчета - в соответствии с преобразованиями Лоренца) и скаляры (инварианты) |
15.1. Релятивистски инвариантное описание при помощи четырехвекторов
| Четырехмерное пространство-время Минковского является псевдоевклидовом, что подразумевает несколько нестандартные (с точки зрения естественного обобщения евклидовой геометрии на четырехмерный случай) определения четырехскалярного произведения и преобразований координат при четырехмерных врадениях. | ||

| (15.1) | Используемые формы записи четырех векторов. |

| (15.2) | Преобразования Лоренца для компонент произвольного четырехвектора. |
15.2. Четырехскорость
| Четырехвектор скорости вводится как производная от описывающего событие четырехмерного аналога радиус-вектора по собственному времени. | ||
 
| (15.3) | Четырехвектор скорости. |

| (15.4) | Проверка свойства инвариантности скалярного произведения четырехвектора скорости на себя. |

| (15.5) | Частный случай преобразования поперечных составляющих скоростей при переходе в движущуюся систему отсчета. |
15.3. Четырехимпульс и четырехсила
| Четырехвектор импульса вводится как произведение четырехвектора скорости на массу покоя частицы; четырехвектор силы - как производная от четырехимпульса по собственному времени. | |||

| (15.6) | Четырехвектор импульса. | |

| (15.7) | Инвариант, составленный из компонент четырехвектора импульса. | |

| (15.8) | Четырехвектор силы. | |

| 
| (15.9) | «Релятивистская масса» и ее зависимость от скорости. |

| (15.10) | Более компактные выражения для четырехимпульса и четырехсилы, записанные с использованием релятивистской массы. | |
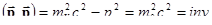
| (15.11) | Квадрат четырехвектора импульса | |
15.4. Релятивистский закон преобразования сил
и основной закон релятивистской динамики
| Преобразования Лоренца для пространственных компонент четырехсилы и четырехимпульса в совокупности с принципом соответствия позволяют получить трехмерное уравнение движения для релятивистской частицы, математическая форма которого весьма сходна со вторым законом Ньютона, записанным в импульсной формулировке. | ||

| (15.12) | Смысл компонент четырехвектора силы в нерелятивистском пределе. |

| Рис. 15.1 Идея расчета результата действия поперечной силы на релятивистскую частицу. | |

| (15.13) | Расчет поперечной составляющей силы в движущейся системе отсчета. |

| (15.14) | Релятивистский аналог второго закона Ньютона для случая силы, действующей перпендикулярно скорости частицы. f’ ^ — сила, действующая на частицу в системе отсчета, где она (частица) покоится. |

| Рис. 15.2 Идея расчета результата действия поперечной силы на релятивистскую частицу. | |

| (15.15) | Расчет продольной составляющей силы в движущейся системе отсчета. |

| (15.16) | Релятивистский аналог второго закона Ньютона для случая силы, действующей в направлении скорости частицы. f’ || — сила, действующая на частицу в системе отсчета, где она (частица) покоится. |

| (15.17) | Трехмерный релятивистский аналог второго закона Ньютона, записанной для системы отсчета, в которой частица не имеет составляющей скорости, нормальной к направлению действия силы. |
15.5. Релятивистская энергия
| Преобразования Лоренца для временных компонент четырехсилы и четырехимпульса в совокупности с принципом соответствия позволяют получить сходное с аналогом из классической физики выражение для энергии релятивистской частицы, значение которого для дальнейшего развития физики и технологий приобрело судьбоносный характер. | ||

| (15.18) | Определение релятивистского импульса и его связь с силой. |

| (15.19) | Аналогичное определению релятивистского импульса определение релятивистской кинетической энергии. |
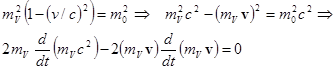
| (15.20) | Простое следствие определения релятивистской массы. |

| (15.21) | Скорость изменения кинетической энергии (результат хорошо согласуется с результатом рассмотрения в классическом пределе (15.12)). |

| (15.22) | Результат интегрирования (15.21). |

| (15.23) | Релятивистское выражение для кинетической энергии. |

| (15.24) | Полная механическая энергия тела в пустом пространстве. |

| (15.25) | Четырехвектор энергии-импульса и релятивистский инвариант, составленный из релятивистских энергии и импульса. |
Пример. Движение релятивистской частицы под действием постоянной силы

| (15.26) | Постановка задачи. |

| (15.27) | Изменение во времени импульса частицы под действием постоянной силы. |

| (15.28) | Вычисление квадрата скорости. |
Пример. Движение частицы под действием силы, явно зависящей от времени.

| (15.26) | Постановка задачи. |

| (15.27) | Изменение во времени импульса частицы под действием постоянной силы. |

| (15.28) | Определение квадрата скорости частицы как функции времени. |

| (15.29) | Решение задачи о скорости релятивистской частицы, движущейся под действием силы, зависящей от времени. |
Вопросы и задачи для самостоятельной работы
- Исходя из преобразований Лоренца, для компонент четырехвектора скорости, получить закон (4.12) сложения продольных составляющих вектора трехмерной скорости.
- Частица, движущаяся с заданной начальной скоростью, начинает испытывать действие постоянной силы, направленной перпендикулярно начальной скорости движения. Определить зависимость от времени скорости частицы.
- Ядро массой M распадается на три одинаковые осколка массами m каждый (M>3m). Определить скорости осколков, если известно, что они одинаковы по величине.
- Рассмотреть движение релятивистской заряженной частицы в однородном магнитном поле.
- Изучить движение релятивистской частицы в сонаправленных электрическом и магнитном полях.
Лекция 16
Движение в неинерциальных системах отсчета
| В рамках нерелятивистской теории уравнение движения классической частицы в неинерциальной системе отсчета может быть получено из второго закона Ньютона с помощью классического закона сложения скоростей |
16.1. Сила инерции
| Уравнение движения нерелятивистской частицы в поступательно движущейся неинерциальной системы отсчета отличается от стандартного закона Ньютона добавлением одного слагаемого традиционно называемого псевдосилой инерции | ||

| (16.1) | Классический закон сложения ускорений |

| (16.2) | Второй закон Ньютона в инерциальной системе отсчета |

| (16.3) | Второй закон Ньютона в неинерциальной системе отсчета |

| (16.4) | Сила инерции |
Пример. «Воздушный шарик» в разгоняющемся автобусе

|

| (16.5) | Силы, действующие на шарик, находящийся в неинерциальной системе отсчета. |

| (16.6) | Эффективное ускорение свободного падения | |

| (16.7) | Угол наклона нити. |
16.2. Силы инерции во вращающихся системах отсчета
| Уравнение движения нерелятивистской частицы во вращающейся (неинерциальной) системе отсчета отличается от стандартного закона Ньютона добавлением двух псевдосил инерции: «центробежной силы» и «кариолисовой силы». | ||

| (16.8) | Правило дифференцирования вектора, изменяющегося во вращающейся системе координат. |

| (16.9) | Классический закон преобразования скоростей в частном случае вращающейся системы отсчета |

| (16.10) | Классический закон преобразования ускорений |

| (16.11) | Скорость изменения скорости движения относительно вращающейся с.о. Второе слагаемое — ускорение тела отн. вращающейся системы. |

| (16.12) | Дифференцирование во втором слагаемом (16.10). |

| (16.13) | Ускорение тела, ускоренно движущегося относительно равномерно вращающейся системы отсчета. |

| (16.14) | Второй закон Ньютона для материальной точки, движущейся во вращающейся системе отсчета |

| (16.15) | Центробежная сила |

| (16.16) | Кариолисова сила |
Пример. Свободное падение тела вблизи поверхности Земли

| (16.17) | Уравнение для определения ускорения тела |

| (16.18) | Вид пробного решения для поиска ответа методом последовательных приближений. |

| (16.19) | Основные этапы решения задачи о свободном падении тела на вращающуюся планету методом последовательных приближений |

| (16.20) | Закон изменения скорости тела, падающего на вращающуюся планету. |

| (16.21) | Движение тела близи поверхности вращающейся планеты. |
16.3. Маятник Фуко
| Поворот плоскости колебаний маятника Фуко с точки зрения наблюдателя, находящегося во вращающейся системе отсчета, связанной с планетой, может быть объяснен действием псевдосил инерции | |||

|

| (16.22) | Сила, испытываемая движущимся маятником Фуко на широте a. |

| (16.23) | Период вращения плоскости колебаний маятника Фуко на широте a. |
16.4. Принцип эквивалентности
и современные представл<