Равновесия в однокомпонентных системах

Тема 1.6. Фазовые равновесия

Основные понятия фазового равновесия. Правило фаз Гиббса

На практике часто приходится иметь дело с гетерогенными системами. Их исследование проводится на основе химической термодинамики, физико-химического анализа и правила фаз. Правило фаз было выведено американским физиком Д. Гиббсом. Оно устанавливает, при каких условиях (Т, Р, С) отдельные однородные участки гетерогенных систем (фазы), находятся в состоянии термодинамического равновесия.

Фазой называют совокупность гомогенных частей системы, обладающих одинаковыми термодинамическими свойствами (т.е. свойствами, зависящими от Т, Р, С и природы взятых веществ) и которые отделены от других частей системы видимыми поверхностями раздела.

Гетерогенные равновесия, т.е. состояния, при которых процесс перехода веществ из одной фазы в другую не сопровождается изменением их химического состава, называются фазовыми равновесиями. К ним относятся:

- испарение,

- конденсация,

- плавление,

- кристаллизация,

- сублимация,

- полиморфные превращения,

- растворение и др.

При изучении фазовых равновесий важно уметь определять число компонентов в равновесных гетерогенных системах. Компонентом называется химически однородная составная часть системы, которая при выделении из системы существует в изолированном виде как угодно долго.

Например, в трехфазной системе:

всего один компонент – вода (Н₂О).

Смесь газов (O₂ + N₂ + H₂) – однофазная система, состоящая из трех компонентов. Каждый из перечисленных газов может длительно существовать в изолированном виде и путем сжижения выделен из системы.

В физических системах (т.е. системах, составные части которых не реагируют друг с другом) число независимых компонентов равно числу составных частей системы (составной частью называется всякое простое вещество или химическое соединение, входящее в систему). В таких системах можно произвольно изменять равновесные концентрации всех составных частей, не вызывая изменения числа и вида фаз в системе, т.е. все составные части системы являются независимыми друг от друга.

В системах, где составные части реагируют друг с другом (химические системы), число независимых компонентов равно числу составных частей минус число химических реакций, протекающих в системе при данных условиях.

Например, равновесная гетерогенная система CaCO₃ «CaO + CO₂ имеет:

3 фазы,

3 составные части,

3-1(химическая реакция)=2 независимых компонента.

Следовательно, концентрацию любых двух из трех веществ, связанных одним уравнением, можно изменять произвольно. Концентрация третьего вещества – величина зависимая и определяется из уравнения реакции.

Чтобы охарактеризовать состояние равновесия той или иной гетерогенной системы, необходимо также знать число степеней свободы. Под числом степеней свободы понимают условия (Т, Р, С), которые можно (до известного предела) произвольно изменять в системе без нарушения состояния равновесия (т.е. без изменения числа и вида фаз).

Например, ненасыщенный пар является системой с двумя степенями свободы (Р и Т), насыщенный – с одной (Р или Т). Ненасыщенный раствор – система, обладающая двумя степенями свободы (Т и С), насыщенный – система с одной степенью свободы (Т или С).

Число фаз Ф, компонентов К и степеней свободы С для случая гетерогенной системы, находящейся в состоянии равновесия, связано уравнением правила фаз:

Ф + С = К + 2

Это уравнение используют для определения числа степеней свободы.

Например, для системы

К = 1, Ф = 3, а С = 0, т.е. нельзя изменить ни одно из условий, не нарушив равновесия.

Для конденсированных систем уравнение принимает вид:

Ф + С = К + 1

В данном случае не учитывается один из факторов – внешнее давление.

Классификация гетерогенных систем:

1. По числу компонентов

- однокомпонентные,

- двухкомпонентные и т.д.

2. По числу степеней свободы (характеризует вариантность системы)

- одновариантные (моновариантные),

- двухвариантные (бивариантные),

- безвариантные (нонвариантные) – при отсутствии степеней свободы.

Равновесия в однокомпонентных системах

К однокомпонентным системам относится любое чистое простое или сложное вещество (сера, железо, вода и пр.)

Произведем анализ однокомпонентных систем, применяя правило фаз, на примере воды. Придавая различные значения числу фаз, определим возможные значения числа степеней свободы:

К = 1 С = 1 + 2 – Ф

При Ф = 1	С = 1 + 2 – 1 = 2 лед, вода или пар – бивариантные системы
При Ф = 2	С = 1 + 2 – 2 = 1 лед«вода, вода«пар, лед«пар – моновариантные системы
При Ф = 3	С = 1 + 2 – 2 = 0 нонвариантная система
При Ф = 4	С = 1 + 2 – 3 = -1 Отрицательная степень свободы, равновесие невозможно

Выводы:

1. При одном компоненте четыре и более фаз находится в равновесии не могут.

2. Наибольшее число степеней свободы в однокомпонентных системах равно 2 (Т и Р, а С = const)/

При изучении гетерогенных равновесий широко пользуются фазовыми диаграммами (диаграммами состояния). Фазовая диаграмма выражает зависимость состояния системы (и фазовых равновесий в них) от внешних условий или состава системы. Диаграмма состояния, построенная в масштабе по опытным данным, позволяет определить состояние системы при любых заданных условиях.

Состояние равновесия в однокомпонентных системах в основном определяется двумя условиями (Р и Т), поэтому диаграммы состояния таких систем являются плоскостными и строятся в координатах Р – Т (см. рис.).

Диаграмма состояния воды

Кривые АО, ОС, ОВ разделяют поле диаграммы на три фазовых поля. Любая точка на каждом из фазовых полей характеризует однофазную систему, обладающую в соответствии с правилом фаз 2-мя степенями свободы (т.е. в пределах фазового поля можно изменять Т и Р, при этом состояние воды не изменится.

Наибольшее давление насыщенного пара (линия ОС) наблюдается при критической температуре воды (374⁰С) и равно 218 атм. Равновесие лед«вода (линия ОВ) наблюдается только до 2000 атм. При более высоких давлениях образуются другие кристаллические модификации льда.

 

D

С

В

А

О

 

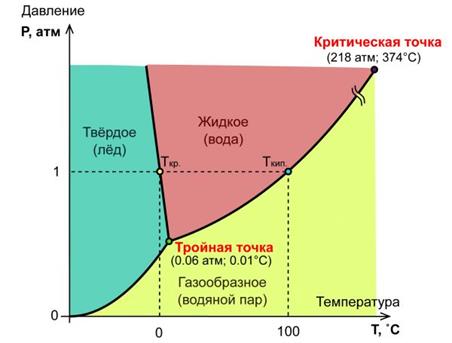
Точки на линиях, разделяющих фазовые поля, характеризуют равновесия двух фаз, при этом система моновариантна.

Фазовые поля сходятся в точке О, называемой тройной точкой. В ней при строго заданных условиях в равновесии находятся три фазы, при этом система безвариантна.

Пунктирная линия ОD характеризует неустойчивое (метастабильное) состояние переохлажденной воды в области устойчивости льда (равновесие переохлажденная вода«пар).

Виды фазовых диаграмм усложняются, если вещество в твердом состоянии образует несколько кристаллических форм, каждая из которых устойчива в определенном интервале температур и давлений и является самостоятельной фазой.