Дифракция на круглом отверстии.
  Возмущение в т.Р будет зависеть от числа зон Френеля, убирающихся в отверстие. Возмущение в т.Р будет зависеть от числа зон Френеля, убирающихся в отверстие.
где R – радиус отверстия.
 Пусть m – нечетное (m = 3) Пусть m – нечетное (m = 3)
А3 – амплитуда колеба-
ний от 3-х зон Френеля.
А 3 ≈ 2·А∞
I3 ≈ 4·I∞
Т.е. для нечетного числа зон Френеля в центре – светлое
пятно и АНЕЧ ≈ 2·А∞ IНЕЧ ≈ 4·I∞

Если открыто четное число зон (например,
m =4), то в центре будет темное пятно.
Если m – не целое (например m = 2,5), то
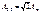
 В т.Р1 будет наложение четного числа зон В т.Р1 будет наложение четного числа зон
и нечетного.
Если их площади ≈, то будет min, т.е. темное пятно. Из-
за симметрии – это будет темное кольцо.
В результате на экране наблюдаем чередование светлых
и темных концентрических колец.
|
|
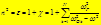 - электронная плазменная частота. - электронная плазменная частота.
- дисперсионное соотношение
Участки 1–2 и 3-4 -
с нормальной дисперсией
Участок 2–3 аномальной
дисперсии.
Он образовался вблизи ω0
из-за сильного поглощения.
 Иначе n2 стремился бы к ± Иначе n2 стремился бы к ±
На участке 3-4 n < 1
т.е. υФ > c. Но энергия
передается с υГР < c.
| Фазовая скорость - зависит от ω.
Т.е. гармоники (спектральные компоненты) распространяются с разными скоростями.
Это приводит к искажению профиля волнового пакета.
Для описания распространения волны одной фазовой скорости недостаточно. Вводят понятие групповой скорости.
Групповая скорость – скорость перемещения энергии волнового пакета.
Т.о., рассматривают две скорости:
- скорость перемещения одинаковой фазы колебаний
- скорость перемещения волнового профиля.
 В среде без дисперсии В среде без дисперсии
Связь между определяется формулой Рэлея:
| Дифракция рентгеновских лучей.
Кристаллическая решетка многих твердых тел может играть роль 3-х мерной дифракционной решетки с периодом d ≈.10-10 м.
 Кристалл рассматр. как сово-купность ║ плоскостей.
Для дифракции необходимо:
d > λ (рентген. диапазон)
λ = 10-8…10-12 м
θ – угол скольжения
Складываются волны, отраженные от всех плоскостей решетки. Если они в фазе, то будет max. Кристалл рассматр. как сово-купность ║ плоскостей.
Для дифракции необходимо:
d > λ (рентген. диапазон)
λ = 10-8…10-12 м
θ – угол скольжения
Складываются волны, отраженные от всех плоскостей решетки. Если они в фазе, то будет max.

- условие max при отражении рентгеновских лучей.
Это формула Брэгга-Вульфа.
Явление используют для спектрального анализа рентгеновского излучения и для исследования структуры кристаллов.
|
25. Эффект Вавилова-Черенкова
 Возникает излучение света заряженной частицей при ее движении со скоростью, большей, чем фазовая скорость света в данной
среде
Наблюдается при движении в прозрачной жидкости быстрых электронов, которые возникают под действием гамма-лучей. Возникает излучение света заряженной частицей при ее движении со скоростью, большей, чем фазовая скорость света в данной
среде
Наблюдается при движении в прозрачной жидкости быстрых электронов, которые возникают под действием гамма-лучей.
 Условия возникн. эффекта В-Ч могут быть объяснены с пом. принципа Гюйгенса-Френеля. Движущийся заряд имеет эл-м поле, которое возбуждает атомы среды на своей траектории. Поэтому каждую точку траектории можно считать источником вторичных волн. В изотропной среде эти волны будут сферическими. Их скорость ССР.
Если υ < ССР, то вторичные волны будут обгонять частицу и взаимного наложения волновых поверхностей (имеющих одинаковую фазу) не происходит.
Если же υ > ССР, то частица обгоняет волны. Сферы начинают пересекаться и интерферировать. Их общая волновая поверхность имеет вид конуса с вершиной в месте, где находится частица. Условия возникн. эффекта В-Ч могут быть объяснены с пом. принципа Гюйгенса-Френеля. Движущийся заряд имеет эл-м поле, которое возбуждает атомы среды на своей траектории. Поэтому каждую точку траектории можно считать источником вторичных волн. В изотропной среде эти волны будут сферическими. Их скорость ССР.
Если υ < ССР, то вторичные волны будут обгонять частицу и взаимного наложения волновых поверхностей (имеющих одинаковую фазу) не происходит.
Если же υ > ССР, то частица обгоняет волны. Сферы начинают пересекаться и интерферировать. Их общая волновая поверхность имеет вид конуса с вершиной в месте, где находится частица.
 Образуется суммарная волна.
Условие ее образования
Эффект В-Ч применяется в ядерной физике для регистрации частиц и для изучения их природы. Образуется суммарная волна.
Условие ее образования
Эффект В-Ч применяется в ядерной физике для регистрации частиц и для изучения их природы.
| 26. Анизотропные диэлектрики.
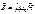    Для анизотропных сред без дисперсии материальные ур-ния имеют вид: и, где Для анизотропных сред без дисперсии материальные ур-ния имеют вид: и, где
 Для немагнитных сред μ = 1, а тензор имеет вид:
εXY = εYX εXZ = εZX εYZ = εZY Для немагнитных сред μ = 1, а тензор имеет вид:
εXY = εYX εXZ = εZX εYZ = εZY
 Тогда Тогда
   В общем случае В общем случае
  ~ ~
Можно найти систему координат, где справедливо:
εX, εY, εZ - главные диэлектр. проницаемости.
 1) Изотропные среды εX = εY = εZ = ε 1) Изотропные среды εX = εY = εZ = ε
 2) Одноосные кристаллы εX = εY ≠ εZ 2) Одноосные кристаллы εX = εY ≠ εZ
3) Двухосные кристаллы εX ≠ εY ≠ εZ
Будем рассматривать одноосные кристаллы с
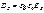
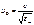  а) Пусть. Т.к. то ЕХ и ЕY - компоненты а) Пусть. Т.к. то ЕХ и ЕY - компоненты
Для любой поляризации. И
 Такое направление распространения (вдоль Z) называют оптической осью. Волна, распространяющаяся вдоль оптич. оси – обыкновенная. Такое направление распространения (вдоль Z) называют оптической осью. Волна, распространяющаяся вдоль оптич. оси – обыкновенная.
- показатель преломления.
| 27. Двойное лучепреломление в одноосном кристалле
Зависимость фазовой скорости плоской волны в анизотропном кристалле от направления распространения волны приводит к тому, что лучи света, преломляясь на поверхности кристалла, раздваиваются. Это явление называют двойным лучепреломлением.
Построение хода лучей в одноосном кристалле
 Рассмотрим преломление плоской волны на границе анизотропного "-" кристалла (ne < n0).
АВ – фронт падающей волны.
1. Вокруг (∙) падения А строим волновые поверх-ти вдоль опт. оси МN (сферу – для норм. волны и эллипсоид – для ненормальной)
2. Проводим к ним касательные из (∙) С(Cо и Се) (по Гюйгенсу – это фронты волн – обыкн. о и н/об. е).
3. Соединяем (∙) падения A и (∙∙) касания.
Это и будут линии хода лучей So и Se
Расстояние АС = с·t
Из рис. видно, что при нормальном падении к опт. оси лучи о и е будут распространяться в том же направлении, но с разными скоростями.
При падении под углом к опт. оси обыкновенный и н/об лучи разойдутся. Произойдет пространственное разделение лучей. Это явление двойного лучепреломления.
Оно используется в поляризаторе на основе призмы Николя.
Примечание. Вдоль опт. оси размер эллипсоида совпадает с размером
сферы. А в ┴ направлении – наибольшая разница.
У "-" кристалла эллипсоид описанный, а у "+" – вписан-
ный в сферу. Рассмотрим преломление плоской волны на границе анизотропного "-" кристалла (ne < n0).
АВ – фронт падающей волны.
1. Вокруг (∙) падения А строим волновые поверх-ти вдоль опт. оси МN (сферу – для норм. волны и эллипсоид – для ненормальной)
2. Проводим к ним касательные из (∙) С(Cо и Се) (по Гюйгенсу – это фронты волн – обыкн. о и н/об. е).
3. Соединяем (∙) падения A и (∙∙) касания.
Это и будут линии хода лучей So и Se
Расстояние АС = с·t
Из рис. видно, что при нормальном падении к опт. оси лучи о и е будут распространяться в том же направлении, но с разными скоростями.
При падении под углом к опт. оси обыкновенный и н/об лучи разойдутся. Произойдет пространственное разделение лучей. Это явление двойного лучепреломления.
Оно используется в поляризаторе на основе призмы Николя.
Примечание. Вдоль опт. оси размер эллипсоида совпадает с размером
сферы. А в ┴ направлении – наибольшая разница.
У "-" кристалла эллипсоид описанный, а у "+" – вписан-
ный в сферу.
|
28. Прохождение плоскополяризованного света через кристал-лическую пластину.
 Луч падает на пластину сверху ┴ пов-ти.
опт. ось пластины Перед пластиной: Луч падает на пластину сверху ┴ пов-ти.
опт. ось пластины Перед пластиной:
 
Вид сверху и - в фазе.
 После пластины: /кристалл - одноосный/ После пластины: /кристалл - одноосный/
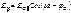
В общем случае на выходе будет
эллиптически поляризованный
 свет. свет.
При
(четверть волновая пластина)

Если
 (полуволновая пластина), то (полуволновая пластина), то
и на выходе будет плоскополя-
ризованный свет как и на входе,
но плоскость поляризации повер-
нется на угол 2θ.
| 29. Понятие макросистемы. Способы их описания.
Макросистема – это система, состоящая из очень большого числа физических объектов. (Газ в сосуде. Объекты – молекулы, атомы.)
Способы описания:
I. Динамический
   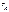 Описание местоположения, траектории и скорости каждого объекта.
II. Статистический (занимается - статистическая физика).
III. Термодинамический. Это самый общий способ.
Термодинамич. величины Р, V, T (занимается – термодинамика)
Фазовое пространство Описание местоположения, траектории и скорости каждого объекта.
II. Статистический (занимается - статистическая физика).
III. Термодинамический. Это самый общий способ.
Термодинамич. величины Р, V, T (занимается – термодинамика)
Фазовое пространство
     Состояние любой частицы газа характеризуется ее положением и импульсом, т.е. 6-ю величинами. Поэтому удобно перейти к 6-ти мерному пространству
и. Его называют фазовым пр-вом.
Его координаты: x, y, z, pX, pY, pZ.
Элемент объема в фазовом пр-ве имеет вид:
dVф = dx·dy·dz·dpX·dpY·dpZ.
Функция распределения Состояние любой частицы газа характеризуется ее положением и импульсом, т.е. 6-ю величинами. Поэтому удобно перейти к 6-ти мерному пространству
и. Его называют фазовым пр-вом.
Его координаты: x, y, z, pX, pY, pZ.
Элемент объема в фазовом пр-ве имеет вид:
dVф = dx·dy·dz·dpX·dpY·dpZ.
Функция распределения
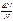  Газ, как система из N частиц, характериз-ся функцией распределения частиц в фазовом пр-ве: Здесь - относительное Газ, как система из N частиц, характериз-ся функцией распределения частиц в фазовом пр-ве: Здесь - относительное
  число частиц
с определ. и число частиц
с определ. и
 Т.к. число N огромно, то относительное число равно вероятности попадания их в объем dVФ: Следовательно, ф-ия
распределения –это плотность Т.к. число N огромно, то относительное число равно вероятности попадания их в объем dVФ: Следовательно, ф-ия
распределения –это плотность
 вероятности:
Свойства ф-ии распределения: вероятности:
Свойства ф-ии распределения:
  1.
2. (т.к. Р = 1). 1.
2. (т.к. Р = 1).
| 30. Фазовое пространство. Функция распределения частиц в нем.
Фазовое пространство
     Состояние любой частицы газа характеризуется ее положением и импульсом, т.е. 6-ю величинами. Поэтому удобно перейти к 6-ти мерному пространству
и. Его называют фазовым пр-вом.
Его координаты: x, y, z, pX, pY, pZ.
Элемент объема в фазовом пр-ве имеет вид:
dVф = dx·dy·dz·dpX·dpY·dpZ.
Функция распределения Состояние любой частицы газа характеризуется ее положением и импульсом, т.е. 6-ю величинами. Поэтому удобно перейти к 6-ти мерному пространству
и. Его называют фазовым пр-вом.
Его координаты: x, y, z, pX, pY, pZ.
Элемент объема в фазовом пр-ве имеет вид:
dVф = dx·dy·dz·dpX·dpY·dpZ.
Функция распределения
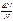  Газ, как система из N частиц, характериз-ся функцией распределения частиц в фазовом пр-ве: Здесь - относительное Газ, как система из N частиц, характериз-ся функцией распределения частиц в фазовом пр-ве: Здесь - относительное
  число частиц
с определ. и число частиц
с определ. и
 Т.к. число N огромно, то относительное число равно вероятности попадания их в объем dVФ: Следовательно, функция
распределения –это плотность Т.к. число N огромно, то относительное число равно вероятности попадания их в объем dVФ: Следовательно, функция
распределения –это плотность
 вероятности:
Свойства ф-ии распределения: вероятности:
Свойства ф-ии распределения:
  1.
2. (т.к. Р = 1). 1.
2. (т.к. Р = 1).
|
31. Понятие термодинамического равновесия (ТДР)
 Если систему предоставить саму себе, то постепенно она будет стремиться к некоторому равновесному состоянию.
При этом Если систему предоставить саму себе, то постепенно она будет стремиться к некоторому равновесному состоянию.
При этом
  Состояние, в котором система может находиться сколь угодно долго без внешнего воздействия, называется равновесным. Всякая система стремится к состоянию равновесия.
ТДР не является равновесием в динамическом смысле: и
постоянно меняются. ТДР – это равновесие в статистическом смысле. Не меняется во времени ф-ия распределения. И как следствие, остаются постоянными макропараметры P, V, T.
Важнейшей хар-кой системы в ТДР является температура Т. В неравновесном состояние понятие t° вообще некорректно использовать. Состояние, в котором система может находиться сколь угодно долго без внешнего воздействия, называется равновесным. Всякая система стремится к состоянию равновесия.
ТДР не является равновесием в динамическом смысле: и
постоянно меняются. ТДР – это равновесие в статистическом смысле. Не меняется во времени ф-ия распределения. И как следствие, остаются постоянными макропараметры P, V, T.
Важнейшей хар-кой системы в ТДР является температура Т. В неравновесном состояние понятие t° вообще некорректно использовать.
| 32. Микро- и макросостояния. Постулат о равновероятностном микросостоянии. Распределение Гиббса.
Макросостояние – состояние, которое хар-ся самыми общими термодинамическими величинами (P, V, T и т.д.)
  Микросостояние хар-ся динамическими величинами, т.е. положе-ниями и скоростями всех n молекул системы. Таких величин будет 6n.
Одному и тому же макросостоянию состоянию соответствует ∞ множество микросостояний.
Все микросостояния системы, соответствующие одинаковой ее полной энергии, равновероятны.
Из данного постулата → распределение Гиббса. Микросостояние хар-ся динамическими величинами, т.е. положе-ниями и скоростями всех n молекул системы. Таких величин будет 6n.
Одному и тому же макросостоянию состоянию соответствует ∞ множество микросостояний.
Все микросостояния системы, соответствующие одинаковой ее полной энергии, равновероятны.
Из данного постулата → распределение Гиббса.
 Имеется изолированная система (в ТДР) с
энергией Е0 = const.
В ней находится некая подсистема с энергией Е. Она взаимодействует с остальной частью системы.
Е – случайная величина и Е<<E0. Имеется изолированная система (в ТДР) с
энергией Е0 = const.
В ней находится некая подсистема с энергией Е. Она взаимодействует с остальной частью системы.
Е – случайная величина и Е<<E0.
 Вероятность того, что энергия подсистемы равна Е:
~
Это каноническое распределение Гиббса.
Вероятность состояния подсистемы зависит только от ее энергии. Вероятность того, что энергия подсистемы равна Е:
~
Это каноническое распределение Гиббса.
Вероятность состояния подсистемы зависит только от ее энергии.
| 33. Нахождение ф-ии распределения идеального газа в состоянии ТДР.
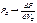  Пусть подсистема – это отдельная частица. Согласно распределению Гиббса вероятность того, что ее энергия равна Е: Пусть подсистема – это отдельная частица. Согласно распределению Гиббса вероятность того, что ее энергия равна Е:
 ~ Из ~, где
dГ – число равновероятных состояний частицы с энергией Е в dVФ.
(dVФ – элементарный объем в фазовом пространстве)
~ Из ~, где
dГ – число равновероятных состояний частицы с энергией Е в dVФ.
(dVФ – элементарный объем в фазовом пространстве)
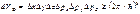  Соотношение неопределенности Гейзенберга: Соотношение неопределенности Гейзенберга:
  где - постоянная Планка. где - постоянная Планка.
 Следовательно - число ячеек с min объемом Следовательно - число ячеек с min объемом
Если число частиц мало по сравнению с числом ячеек, то
Это классический (идеальный) газ.
 Тогда Тогда
~
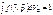
 Коэффициент С можно найти из условия нормировки Коэффициент С можно найти из условия нормировки
 Окончательно, ф-ия распределения идеального газа, Окончательно, ф-ия распределения идеального газа,
находящегося в состоянии ТДР, имеет вид:
 Если газ более плотный (не идеальный), то Если газ более плотный (не идеальный), то
и ф-ия распределения будет другой.
|
| 34. Распределение Максвелла. Вычисление средних характеристик молекул газа в состоянии ТДР.
Распределение М. – это распределение по импульсам (или скоростям) молекул системы в состоянии ТДР.
Согласно распределению Максвелла, вероятность того, что проекции импульса молекулы лежат в интервале от рX до рX+dрX, от рY до рY+dрY, от рZ до рZ+dрZ определяется формулой:
где m – масса молекулы; k – постоянная Больцмана.
 Вероятность того, что модуль скорости лежит в интервале от υ до υ+dυ имеет вид: Вероятность того, что модуль скорости лежит в интервале от υ до υ+dυ имеет вид:
Максимума эта ф-ия достигает при - наиболее вероятная скорость молекул.
Среднее число молекул в 1 см3, имеющих скорости от υ до υ+dυ равно n(υ) = n0·f(υ), где n0 – полное число молекул в 1 см3.
 Средняя квадратичная скорость молекул Средняя квадратичная скорость молекул
Это всего в 1,22 раза больше υ0.
Распределение Максвелла не зависит от взаимодействия частиц системы и от внешних сил. Поэтому оно применимо не только к газам, но и к жидкостям и твердым телам. Применимо оно и для броуновских частиц, взвешенных в газе или жидкости.
| 35. Распределение Больцмана.
Распределение Б. – это вероятность нахождения молекул идеального газа, находящихся в потенциальном поле внешних сил.
Энергия частиц газа равна сумме:
 где -кинетическая энергия частиц где -кинетическая энергия частиц
Е ВЗАИМОД – энергия взаимодействия частиц. Для идеального газа = 0.
ЕП(r) - потенциальная энергия во внешнем поле.
 Тогда и распределение М-Б* примет вид: Тогда и распределение М-Б* примет вид:
Таким образом, ф-ия распределения есть произведение вероятностей 2-х независимых событий: 1) вероятности данного значения импульса молекулы (распределение Максвелла); 2) вероятности данного положения в пространстве (распределение Больцмана).
 Распр. Больцмана можно найти. Распр. Больцмана можно найти.
 - концентрация. – относительное число молекул в dV - концентрация. – относительное число молекул в dV
 По распределению Больцмана: По распределению Больцмана:
Например, в поле тяжести Еп = mgz, тогда
где n0 = n при z = 0.
С высотой концентрация молекул убывает.
Кол-во молекул dN в слое dz: dN = n(z)·S·dz где S – площадь слоя.

* М-Б - Максвелла-Больцмана.
| 36. Теорема о равнораспределении энергии по степеням свободы
Число степеней свободы системы – это число независимых переменных, определяющих положение системы в пространстве. Обозначается i.
Например, для свободной материальной точки i =3;
для молекулы одноатомного газа i =3;
для N молекул i =3·N;
для молекулы 2-х атомного газа i =5;
для молекул твердого тела i =6;
для осциллятора i =2.
В состоянии термодинамического равновесия (ТДР) на каждую степень свободы системы приходится ½ kT энергии.
|
|
|   б) Пусть, например, k = kХ. Тогда и б) Пусть, например, k = kХ. Тогда и
  Волны с будут иметь. Это обыкновенные волны.
Волны с будут иметь. Это обыкновенные волны.
   А волны с Е (ЕZ) – необыкновенные.
У них показатель преломления и А волны с Е (ЕZ) – необыкновенные.
У них показатель преломления и
  в) Произвольное направление в) Произвольное направление
Будет два луча: обыкновенный с, и необыкновенный с
(если n0 > ne) либо (если n0 < ne).
Поместим источник света в начало координат (внутри кристалла).
n0 > ne - отрицательные кристаллы. n0 < ne - положительные
Пример – исландский шпат. кристаллы (кварц)
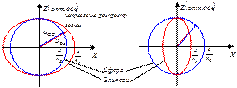
Главная оптич. плоскость совпадает с плоскостью рисунка.
Волновой поверхностью обыкновенной волны является сфера (υ=const), а необыкновенной – эллипсоид. Скорость зависит от направления.
Наибольшее расхождение скоростей обыкн. и необыкн. волн будет в направлении ┴ оптической оси.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37. Понятие фотона. Тепловое излучение
Атомы имеют энергетические уровни, на которых находятся электроны. При переходе электрона с одного уровня на другой происходит поглощение или излучение энергии. Т.к. уровни дискретны, то и энергия перехода между соседними уровнями тоже дискретна и равна ΔW.
При переходе электрона на соседний уровень атом поглощает (испускает) минимальную порцию света – квант, называемую фотоном. Его энергия ε = ΔW.
  В тепловом излучении такой переход осуществляется в результате теплового движения атомов и молекул, их взаимодействия. В тепловом излучении такой переход осуществляется в результате теплового движения атомов и молекул, их взаимодействия.
 Как частица фотон имеет ε (энергию) и (импульс).
Как волна – ω (частоту колебаний)и (волновой вектор)
Корпускулярные и волновые характеристики излучения связаны с помощью формул: Как частица фотон имеет ε (энергию) и (импульс).
Как волна – ω (частоту колебаний)и (волновой вектор)
Корпускулярные и волновые характеристики излучения связаны с помощью формул:
   - постоянная Планка.
Тепловое излучение изотропно и неполяризовано, т.е. направления излучения равновероятны и направления векторов Е и В в каждой точке меняется во времени хаотично. - постоянная Планка.
Тепловое излучение изотропно и неполяризовано, т.е. направления излучения равновероятны и направления векторов Е и В в каждой точке меняется во времени хаотично.
| 38. Характеристики теплового излучения. Закон Кирхгофа. Формула Рэлея Джинса
 Характеристики теплового излучения
1. Излучательная способность
где dW – энергия, излучаемая с поверхности dS за время dt в диапазоне частот dω.
Тепловое излучение происходит на всех частотах, т.е. его спектр – Характеристики теплового излучения
1. Излучательная способность
где dW – энергия, излучаемая с поверхности dS за время dt в диапазоне частот dω.
Тепловое излучение происходит на всех частотах, т.е. его спектр –
 сплошной.
2. Энергетическая светимость сплошной.
2. Энергетическая светимость
 3. Поглощающая способность - это доля поглощаемой энергии от падающей энергии (остальная часть отражается). 3. Поглощающая способность - это доля поглощаемой энергии от падающей энергии (остальная часть отражается).
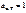 У абсолютно черного тела У абсолютно черного тела
Закон Кирхгофа
Устанавливает связь между излучательной и поглощающей способностью тела.
 - функция Кирхгофа. По з-ну Кирхгофа это отношение для произвольных частот и температур одинаково для всех тел и равно излучательной способности абсолют. черного тела. - функция Кирхгофа. По з-ну Кирхгофа это отношение для произвольных частот и температур одинаково для всех тел и равно излучательной способности абсолют. черного тела.
Отсюда следует, что, если тело при данной t° не поглощает излучение в каком-то диапазоне ω+Δω, то оно не может и излучать в нем при этой t°, т.к. r = a·f = 0·f = 0.
Если раскаленное тело находится в раскаленной печи, то все его участки светятся одинаково, т.к. в печи установилось состояние равновесия.
Если же тело вне печи, то равновесия нет и яркость темных участков тела будет больше, чем светлых (r = a·f, а – больше у темного тела).
| 39. Излучение абсолютно черного тела. Формула Планка.
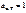 Абсолютно чёрное тело - тело, которое при любой t° полностью поглощает весь падающий на него поток излучения, независимо от длины волны λ. Коэффициент поглощения. В природе А.Ч.Т. нет. Близким к 1 коэфф-том поглощения обладает сажа. Абсолютно чёрное тело - тело, которое при любой t° полностью поглощает весь падающий на него поток излучения, независимо от длины волны λ. Коэффициент поглощения. В природе А.Ч.Т. нет. Близким к 1 коэфф-том поглощения обладает сажа.
 Наилучшим приближением к А.Ч.Т. является почти
замкнутый сосуд с малым отверстием и непроз-
рачными стенками, имеющими одинаковую t°
во всех точках. Луч, попавший в полость через
отверстие, многократно отражается и при
каждом отражении частично поглощается
стенками полости. В результате через некоторое
время он поглотится почти полностью.
А.Ч.Т., как и все нагретые тела, испускает электромагнитное излучение. Основной особенностью А.Ч.Т. является то, что его спектр излучения определяется только t° и не зависит от свойств вещества, из которого оно состоит.
Яркость А.Ч.Т. чрезвычайно быстро возрастает с t°. Зависимость яркости и цвета А.Ч.Т. от t° определяется законами излучения Стефана — Больцмана, Вина и Планка. Эти законы позволяют определять t° А.Ч.Т. по характеру их излучения. Такие измерения производятся пирометрами.
Яркость А.Ч.Т. для данной t° — величина постоянная, большая, чем яркость любого другого тела (серого тела) при той же t°, поэтому А.Ч.Т. применяют в качестве светового эталона. Наилучшим приближением к А.Ч.Т. является почти
замкнутый сосуд с малым отверстием и непроз-
рачными стенками, имеющими одинаковую t°
во всех точках. Луч, попавший в полость через
отверстие, многократно отражается и при
каждом отражении частично поглощается
стенками полости. В результате через некоторое
время он поглотится почти полностью.
А.Ч.Т., как и все нагретые тела, испускает электромагнитное излучение. Основной особенностью А.Ч.Т. является то, что его спектр излучения определяется только t° и не зависит от свойств вещества, из которого оно состоит.
Яркость А.Ч.Т. чрезвычайно быстро возрастает с t°. Зависимость яркости и цвета А.Ч.Т. от t° определяется законами излучения Стефана — Больцмана, Вина и Планка. Эти законы позволяют определять t° А.Ч.Т. по характеру их излучения. Такие измерения производятся пирометрами.
Яркость А.Ч.Т. для данной t° — величина постоянная, большая, чем яркость любого другого тела (серого тела) при той же t°, поэтому А.Ч.Т. применяют в качестве светового эталона.
 Согласно з-ну Планка, объемная плотность излучения (т.е. энергия излучения в единице объема): Согласно з-ну Планка, объемная плотность излучения (т.е. энергия излучения в единице объема):
 - излучательная способность; с – скорость света в вакууме;
- излучательная способность; с – скорость света в вакууме;
 - постоянная Планка; k – постоянная Больцмана;
λ – длина волны излучения. - постоянная Планка; k – постоянная Больцмана;
λ – длина волны излучения.
|
40. Закон смещения Вина. Закон Стефана-Больцмана.
Закон смещения Вина - закон, утверждающий, что длина волны λмакс, на которую приходится максимум энергии в спектре равновесного излучения, обратно пропорциональна абсолютной температуре Т излучающего тела: λмакс·Т = b, где b = 0,2897 см·К.
Он объясняет смещение спектра остывающего тела в длинно-волновую область спектра.
 Закон излучения Стефана-Больцмана устанавливае связь между температурой абсолютно черного тела и его излучательной способностью:
где σ – постоянная Стефана-Больцмана. σ = 5,67·10-8 Вт/(м2·К)
Эта зависимость применяется при измерении высоких температур в пирометрах.
Оба закона получены экспериментально. Потом оказалось, что они следствия из закона излучения Планка. Закон излучения Стефана-Больцмана устанавливае связь между температурой абсолютно черного тела и его излучательной способностью:
где σ – постоянная Стефана-Больцмана. σ = 5,67·10-8 Вт/(м2·К)
Эта зависимость применяется при измерении высоких температур в пирометрах.
Оба закона получены экспериментально. Потом оказалось, что они следствия из закона излучения Планка.
|
|
|
|
|
|
|
|
|
|
|
|
| Формула Рэлея-Джинса
По ней можно найти излучательную способность абсолютно черного тела.
Его излучение представляется в виде набора независимых эл-магн. волн различной частоты ω (набор осцилляторов ω).
 На каждый такой осциллятор в ТДР приходится kT энергии. Просуммировав по всем осцилляторам, получим:
На малых частотах эта ф-ла хорошо согласуется
с экспериментальными данными, а на больших На каждый такой осциллятор в ТДР приходится kT энергии. Просуммировав по всем осцилляторам, получим:
На малых частотах эта ф-ла хорошо согласуется
с экспериментальными данными, а на больших
 приводит к расхождению. Это так называемая "ультрафиолетовая катастрофа" приводит к расхождению. Это так называемая "ультрафиолетовая катастрофа"
|
|

 Возмущение в т.Р будет зависеть от числа зон Френеля, убирающихся в отверстие.
Возмущение в т.Р будет зависеть от числа зон Френеля, убирающихся в отверстие. Пусть m – нечетное (m = 3)
Пусть m – нечетное (m = 3)
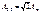
 В т.Р1 будет наложение четного числа зон
В т.Р1 будет наложение четного числа зон

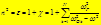 - электронная плазменная частота.
- электронная плазменная частота.
 Иначе n2 стремился бы к ±
Иначе n2 стремился бы к ±
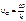


 В среде без дисперсии
В среде без дисперсии
 Кристалл рассматр. как сово-купность ║ плоскостей.
Для дифракции необходимо:
d > λ (рентген. диапазон)
λ = 10-8…10-12 м
θ – угол скольжения
Складываются волны, отраженные от всех плоскостей решетки. Если они в фазе, то будет max.
Кристалл рассматр. как сово-купность ║ плоскостей.
Для дифракции необходимо:
d > λ (рентген. диапазон)
λ = 10-8…10-12 м
θ – угол скольжения
Складываются волны, отраженные от всех плоскостей решетки. Если они в фазе, то будет max.
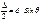


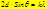
 Возникает излучение света заряженной частицей при ее движении со скоростью, большей, чем фазовая скорость света в данной
среде
Наблюдается при движении в прозрачной жидкости быстрых электронов, которые возникают под действием гамма-лучей.
Возникает излучение света заряженной частицей при ее движении со скоростью, большей, чем фазовая скорость света в данной
среде
Наблюдается при движении в прозрачной жидкости быстрых электронов, которые возникают под действием гамма-лучей.
 Условия возникн. эффекта В-Ч могут быть объяснены с пом. принципа Гюйгенса-Френеля. Движущийся заряд имеет эл-м поле, которое возбуждает атомы среды на своей траектории. Поэтому каждую точку траектории можно считать источником вторичных волн. В изотропной среде эти волны будут сферическими. Их скорость ССР.
Если υ < ССР, то вторичные волны будут обгонять частицу и взаимного наложения волновых поверхностей (имеющих одинаковую фазу) не происходит.
Если же υ > ССР, то частица обгоняет волны. Сферы начинают пересекаться и интерферировать. Их общая волновая поверхность имеет вид конуса с вершиной в месте, где находится частица.
Условия возникн. эффекта В-Ч могут быть объяснены с пом. принципа Гюйгенса-Френеля. Движущийся заряд имеет эл-м поле, которое возбуждает атомы среды на своей траектории. Поэтому каждую точку траектории можно считать источником вторичных волн. В изотропной среде эти волны будут сферическими. Их скорость ССР.
Если υ < ССР, то вторичные волны будут обгонять частицу и взаимного наложения волновых поверхностей (имеющих одинаковую фазу) не происходит.
Если же υ > ССР, то частица обгоняет волны. Сферы начинают пересекаться и интерферировать. Их общая волновая поверхность имеет вид конуса с вершиной в месте, где находится частица.
 Образуется суммарная волна.
Условие ее образования
Эффект В-Ч применяется в ядерной физике для регистрации частиц и для изучения их природы.
Образуется суммарная волна.
Условие ее образования
Эффект В-Ч применяется в ядерной физике для регистрации частиц и для изучения их природы.
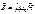


 Для анизотропных сред без дисперсии материальные ур-ния имеют вид: и, где
Для анизотропных сред без дисперсии материальные ур-ния имеют вид: и, где
 Для немагнитных сред μ = 1, а тензор имеет вид:
εXY = εYX εXZ = εZX εYZ = εZY
Для немагнитных сред μ = 1, а тензор имеет вид:
εXY = εYX εXZ = εZX εYZ = εZY
 Тогда
Тогда


 В общем случае
В общем случае

 ~
~


 1) Изотропные среды εX = εY = εZ = ε
1) Изотропные среды εX = εY = εZ = ε 2) Одноосные кристаллы εX = εY ≠ εZ
2) Одноосные кристаллы εX = εY ≠ εZ
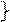

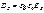



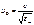
 а) Пусть. Т.к. то ЕХ и ЕY - компоненты
а) Пусть. Т.к. то ЕХ и ЕY - компоненты Такое направление распространения (вдоль Z) называют оптической осью. Волна, распространяющаяся вдоль оптич. оси – обыкновенная.
Такое направление распространения (вдоль Z) называют оптической осью. Волна, распространяющаяся вдоль оптич. оси – обыкновенная. Рассмотрим преломление плоской волны на границе анизотропного "-" кристалла (ne < n0).
АВ – фронт падающей волны.
1. Вокруг (∙) падения А строим волновые поверх-ти вдоль опт. оси МN (сферу – для норм. волны и эллипсоид – для ненормальной)
2. Проводим к ним касательные из (∙) С(Cо и Се) (по Гюйгенсу – это фронты волн – обыкн. о и н/об. е).
3. Соединяем (∙) падения A и (∙∙) касания.
Это и будут линии хода лучей So и Se
Расстояние АС = с·t
Из рис. видно, что при нормальном падении к опт. оси лучи о и е будут распространяться в том же направлении, но с разными скоростями.
При падении под углом к опт. оси обыкновенный и н/об лучи разойдутся. Произойдет пространственное разделение лучей. Это явление двойного лучепреломления.
Оно используется в поляризаторе на основе призмы Николя.
Примечание. Вдоль опт. оси размер эллипсоида совпадает с размером
сферы. А в ┴ направлении – наибольшая разница.
У "-" кристалла эллипсоид описанный, а у "+" – вписан-
ный в сферу.
Рассмотрим преломление плоской волны на границе анизотропного "-" кристалла (ne < n0).
АВ – фронт падающей волны.
1. Вокруг (∙) падения А строим волновые поверх-ти вдоль опт. оси МN (сферу – для норм. волны и эллипсоид – для ненормальной)
2. Проводим к ним касательные из (∙) С(Cо и Се) (по Гюйгенсу – это фронты волн – обыкн. о и н/об. е).
3. Соединяем (∙) падения A и (∙∙) касания.
Это и будут линии хода лучей So и Se
Расстояние АС = с·t
Из рис. видно, что при нормальном падении к опт. оси лучи о и е будут распространяться в том же направлении, но с разными скоростями.
При падении под углом к опт. оси обыкновенный и н/об лучи разойдутся. Произойдет пространственное разделение лучей. Это явление двойного лучепреломления.
Оно используется в поляризаторе на основе призмы Николя.
Примечание. Вдоль опт. оси размер эллипсоида совпадает с размером
сферы. А в ┴ направлении – наибольшая разница.
У "-" кристалла эллипсоид описанный, а у "+" – вписан-
ный в сферу.
 Луч падает на пластину сверху ┴ пов-ти.
опт. ось пластины Перед пластиной:
Луч падает на пластину сверху ┴ пов-ти.
опт. ось пластины Перед пластиной:




 После пластины: /кристалл - одноосный/
После пластины: /кристалл - одноосный/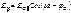

 свет.
свет.


 (полуволновая пластина), то
(полуволновая пластина), то


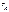 Описание местоположения, траектории и скорости каждого объекта.
II. Статистический (занимается - статистическая физика).
III. Термодинамический. Это самый общий способ.
Термодинамич. величины Р, V, T (занимается – термодинамика)
Фазовое пространство
Описание местоположения, траектории и скорости каждого объекта.
II. Статистический (занимается - статистическая физика).
III. Термодинамический. Это самый общий способ.
Термодинамич. величины Р, V, T (занимается – термодинамика)
Фазовое пространство



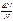
 Газ, как система из N частиц, характериз-ся функцией распределения частиц в фазовом пр-ве: Здесь - относительное
Газ, как система из N частиц, характериз-ся функцией распределения частиц в фазовом пр-ве: Здесь - относительное
 Т.к. число N огромно, то относительное число равно вероятности попадания их в объем dVФ: Следовательно, ф-ия
распределения –это плотность
Т.к. число N огромно, то относительное число равно вероятности попадания их в объем dVФ: Следовательно, ф-ия
распределения –это плотность
 вероятности:
Свойства ф-ии распределения:
вероятности:
Свойства ф-ии распределения:

 1.
2. (т.к. Р = 1).
1.
2. (т.к. Р = 1).
 Если систему предоставить саму себе, то постепенно она будет стремиться к некоторому равновесному состоянию.
При этом
Если систему предоставить саму себе, то постепенно она будет стремиться к некоторому равновесному состоянию.
При этом

 Состояние, в котором система может находиться сколь угодно долго без внешнего воздействия, называется равновесным. Всякая система стремится к состоянию равновесия.
ТДР не является равновесием в динамическом смысле: и
постоянно меняются. ТДР – это равновесие в статистическом смысле. Не меняется во времени ф-ия распределения. И как следствие, остаются постоянными макропараметры P, V, T.
Важнейшей хар-кой системы в ТДР является температура Т. В неравновесном состояние понятие t° вообще некорректно использовать.
Состояние, в котором система может находиться сколь угодно долго без внешнего воздействия, называется равновесным. Всякая система стремится к состоянию равновесия.
ТДР не является равновесием в динамическом смысле: и
постоянно меняются. ТДР – это равновесие в статистическом смысле. Не меняется во времени ф-ия распределения. И как следствие, остаются постоянными макропараметры P, V, T.
Важнейшей хар-кой системы в ТДР является температура Т. В неравновесном состояние понятие t° вообще некорректно использовать.

 Имеется изолированная система (в ТДР) с
энергией Е0 = const.
В ней находится некая подсистема с энергией Е. Она взаимодействует с остальной частью системы.
Е – случайная величина и Е<<E0.
Имеется изолированная система (в ТДР) с
энергией Е0 = const.
В ней находится некая подсистема с энергией Е. Она взаимодействует с остальной частью системы.
Е – случайная величина и Е<<E0.
 Вероятность того, что энергия подсистемы равна Е:
~
Это каноническое распределение Гиббса.
Вероятность состояния подсистемы зависит только от ее энергии.
Вероятность того, что энергия подсистемы равна Е:
~
Это каноническое распределение Гиббса.
Вероятность состояния подсистемы зависит только от ее энергии.
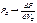
 Пусть подсистема – это отдельная частица. Согласно распределению Гиббса вероятность того, что ее энергия равна Е:
Пусть подсистема – это отдельная частица. Согласно распределению Гиббса вероятность того, что ее энергия равна Е:
 ~ Из ~, где
dГ – число равновероятных состояний частицы с энергией Е в dVФ.
(dVФ – элементарный объем в фазовом пространстве)
~ Из ~, где
dГ – число равновероятных состояний частицы с энергией Е в dVФ.
(dVФ – элементарный объем в фазовом пространстве)
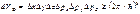
 Соотношение неопределенности Гейзенберга:
Соотношение неопределенности Гейзенберга:

 где - постоянная Планка.
где - постоянная Планка.
 Следовательно - число ячеек с min объемом
Следовательно - число ячеек с min объемом

 Тогда
Тогда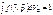
 Коэффициент С можно найти из условия нормировки
Коэффициент С можно найти из условия нормировки Окончательно, ф-ия распределения идеального газа,
Окончательно, ф-ия распределения идеального газа, Если газ более плотный (не идеальный), то
Если газ более плотный (не идеальный), то
 Вероятность того, что модуль скорости лежит в интервале от υ до υ+dυ имеет вид:
Вероятность того, что модуль скорости лежит в интервале от υ до υ+dυ имеет вид:
 Средняя квадратичная скорость молекул
Средняя квадратичная скорость молекул
 где -кинетическая энергия частиц
где -кинетическая энергия частиц Тогда и распределение М-Б* примет вид:
Тогда и распределение М-Б* примет вид:
 Распр. Больцмана можно найти.
Распр. Больцмана можно найти.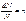

 - концентрация. – относительное число молекул в dV
- концентрация. – относительное число молекул в dV По распределению Больцмана:
По распределению Больцмана:


 б) Пусть, например, k = kХ. Тогда и
б) Пусть, например, k = kХ. Тогда и

 Волны с будут иметь. Это обыкновенные волны.
Волны с будут иметь. Это обыкновенные волны.


 А волны с Е (ЕZ) – необыкновенные.
У них показатель преломления и
А волны с Е (ЕZ) – необыкновенные.
У них показатель преломления и




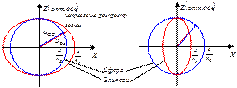


 - постоянная Планка.
Тепловое излучение изотропно и неполяризовано, т.е. направления излучения равновероятны и направления векторов Е и В в каждой точке меняется во времени хаотично.
- постоянная Планка.
Тепловое излучение изотропно и неполяризовано, т.е. направления излучения равновероятны и направления векторов Е и В в каждой точке меняется во времени хаотично.
 Характеристики теплового излучения
1. Излучательная способность
где dW – энергия, излучаемая с поверхности dS за время dt в диапазоне частот dω.
Тепловое излучение происходит на всех частотах, т.е. его спектр –
Характеристики теплового излучения
1. Излучательная способность
где dW – энергия, излучаемая с поверхности dS за время dt в диапазоне частот dω.
Тепловое излучение происходит на всех частотах, т.е. его спектр –
 сплошной.
2. Энергетическая светимость
сплошной.
2. Энергетическая светимость

 3. Поглощающая способность - это доля поглощаемой энергии от падающей энергии (остальная часть отражается).
3. Поглощающая способность - это доля поглощаемой энергии от падающей энергии (остальная часть отражается).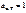 У абсолютно черного тела
У абсолютно черного тела - функция Кирхгофа. По з-ну Кирхгофа это отношение для произвольных частот и температур одинаково для всех тел и равно излучательной способности абсолют. черного тела.
- функция Кирхгофа. По з-ну Кирхгофа это отношение для произвольных частот и температур одинаково для всех тел и равно излучательной способности абсолют. черного тела. Наилучшим приближением к А.Ч.Т. является почти
замкнутый сосуд с малым отверстием и непроз-
рачными стенками, имеющими одинаковую t°
во всех точках. Луч, попавший в полость через
отверстие, многократно отражается и при
каждом отражении частично поглощается
стенками полости. В результате через некоторое
время он поглотится почти полностью.
А.Ч.Т., как и все нагретые тела, испускает электромагнитное излучение. Основной особенностью А.Ч.Т. является то, что его спектр излучения определяется только t° и не зависит от свойств вещества, из которого оно состоит.
Яркость А.Ч.Т. чрезвычайно быстро возрастает с t°. Зависимость яркости и цвета А.Ч.Т. от t° определяется законами излучения Стефана — Больцмана, Вина и Планка. Эти законы позволяют определять t° А.Ч.Т. по характеру их излучения. Такие измерения производятся пирометрами.
Яркость А.Ч.Т. для данной t° — величина постоянная, большая, чем яркость любого другого тела (серого тела) при той же t°, поэтому А.Ч.Т. применяют в качестве светового эталона.
Наилучшим приближением к А.Ч.Т. является почти
замкнутый сосуд с малым отверстием и непроз-
рачными стенками, имеющими одинаковую t°
во всех точках. Луч, попавший в полость через
отверстие, многократно отражается и при
каждом отражении частично поглощается
стенками полости. В результате через некоторое
время он поглотится почти полностью.
А.Ч.Т., как и все нагретые тела, испускает электромагнитное излучение. Основной особенностью А.Ч.Т. является то, что его спектр излучения определяется только t° и не зависит от свойств вещества, из которого оно состоит.
Яркость А.Ч.Т. чрезвычайно быстро возрастает с t°. Зависимость яркости и цвета А.Ч.Т. от t° определяется законами излучения Стефана — Больцмана, Вина и Планка. Эти законы позволяют определять t° А.Ч.Т. по характеру их излучения. Такие измерения производятся пирометрами.
Яркость А.Ч.Т. для данной t° — величина постоянная, большая, чем яркость любого другого тела (серого тела) при той же t°, поэтому А.Ч.Т. применяют в качестве светового эталона.
 Согласно з-ну Планка, объемная плотность излучения (т.е. энергия излучения в единице объема):
Согласно з-ну Планка, объемная плотность излучения (т.е. энергия излучения в единице объема):
 - излучательная способность; с – скорость света в вакууме;
- излучательная способность; с – скорость света в вакууме;
 Закон излучения Стефана-Больцмана устанавливае связь между температурой абсолютно черного тела и его излучательной способностью:
где σ – постоянная Стефана-Больцмана. σ = 5,67·10-8 Вт/(м2·К)
Эта зависимость применяется при измерении высоких температур в пирометрах.
Оба закона получены экспериментально. Потом оказалось, что они следствия из закона излучения Планка.
Закон излучения Стефана-Больцмана устанавливае связь между температурой абсолютно черного тела и его излучательной способностью:
где σ – постоянная Стефана-Больцмана. σ = 5,67·10-8 Вт/(м2·К)
Эта зависимость применяется при измерении высоких температур в пирометрах.
Оба закона получены экспериментально. Потом оказалось, что они следствия из закона излучения Планка.
 На каждый такой осциллятор в ТДР приходится kT энергии. Просуммировав по всем осцилляторам, получим:
На малых частотах эта ф-ла хорошо согласуется
с экспериментальными данными, а на больших
На каждый такой осциллятор в ТДР приходится kT энергии. Просуммировав по всем осцилляторам, получим:
На малых частотах эта ф-ла хорошо согласуется
с экспериментальными данными, а на больших
 приводит к расхождению. Это так называемая "ультрафиолетовая катастрофа"
приводит к расхождению. Это так называемая "ультрафиолетовая катастрофа"