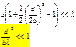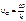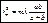Основные частотные диапазоны эл-м волн
| λ, м
| 1011 106 10-3 10 -7 760-400 нм 10 -8 10 -9 10 -13
| | ν, Гц
| 3∙10-3 3∙102 3∙1011 3∙1015 (3,9-7,5)∙1014 3∙1016 3∙1017 3∙1021
| | назв
| НЧ волн
| радиоволн
| ИК
лучи
| видимый свет
| УФ
| рентген
| γ - излучение
| | кто
| ген ~ток
| р/передат
| тепло
|
|
|
|
| | для
| гидроакк
| связь
| в темн.
|
| медиц
| медиц
| строение
вещ-ва
|
|
|
9. Коэффициенты отражения и пропускания при нормальном падении волны на границу 2-х диэлектриков
  I – интенсивность света – средняя по времени энергия, переносимая э-м волной через ед. площадку, ┴ к направлению распространения волны в единицу t. Для света. где S –вектор Умова-Пойтинга I – интенсивность света – средняя по времени энергия, переносимая э-м волной через ед. площадку, ┴ к направлению распространения волны в единицу t. Для света. где S –вектор Умова-Пойтинга
- коэффициент отражения. – коэфф-нт пропускания.
Из условия непрерывности Еτ на границе (y=0): (1)
Из условия непрерывности Нτ на границе (y=0):
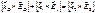
  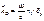
 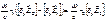 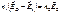
(2)
 Из (1) и (2) имеем (при y=0): Из (1) и (2) имеем (при y=0):
 При отражении от оптически более плотной среды происходит изменение фазы на π. При отражении от оптически более плотной среды происходит изменение фазы на π.
 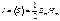
~
где - относительный пок-ль 2-й ср. по отн. к 1-й. ρ ≠ τ
|
|
|
  2) Тогда и
2) Тогда и
  I = I1 + I2 (независимо от Δφ)
I = I1 + I2 (независимо от Δφ)
3) Общий случай – произвольное направление
 Интерференция – сложение колебаний, при котором происходит перераспределение энергии светового потока и могут наблюдаться минимумы и максимумы интенсивности. Интерференция – сложение колебаний, при котором происходит перераспределение энергии светового потока и могут наблюдаться минимумы и максимумы интенсивности.
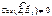 Наблюдается при зависимости фаз колебаний (т.е. CosΔφ ≠ 0) и не-перпендикулярности векторов Е (т.е.). Наблюдается при зависимости фаз колебаний (т.е. CosΔφ ≠ 0) и не-перпендикулярности векторов Е (т.е.).
|
| Поляризаторы
П. – устройства или приборы, с пом. которых можно получить поляризованный свет.
На выходе идеального П. получается линейный плоскополяризованный свет. На выходе неидеального П. – еще и частично неполяризованный свет.
 Принцип действия Принцип действия
 П. свободно пропускает колебания с вектором, лежащим в одной плоскости, называемой пл. поляризатора (ПП). П. свободно пропускает колебания с вектором, лежащим в одной плоскости, называемой пл. поляризатора (ПП).
 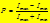 Если пл. колебаний вектора лежит в ПП, то волна проходит полностью. Если пл. колебаний ПП, то волна не проходит. В остальных случаях волна проходит частично.
- степень поляризации, где Imax и Imin - макс и мин
возможные интенсивности.
0 ≤Р≤ 1 Р = 0 – естественный свет; Р = 1 – плоскополяризованный свет.
Закон Малюса (для плоскополяриз. света)
Пусть на идеал. П. падает плоскополяр. свет и угол между пл. колебаний падающего света и ПП = φ.
Тогда интенсивность света на выходе IВЫХ = IВХ∙Сos2φ Если пл. колебаний вектора лежит в ПП, то волна проходит полностью. Если пл. колебаний ПП, то волна не проходит. В остальных случаях волна проходит частично.
- степень поляризации, где Imax и Imin - макс и мин
возможные интенсивности.
0 ≤Р≤ 1 Р = 0 – естественный свет; Р = 1 – плоскополяризованный свет.
Закон Малюса (для плоскополяриз. света)
Пусть на идеал. П. падает плоскополяр. свет и угол между пл. колебаний падающего света и ПП = φ.
Тогда интенсивность света на выходе IВЫХ = IВХ∙Сos2φ
|
13. Оптическая разность хода. Условия min и max при
интерференции 2-х волн.
 - для волн одного направления
и естественного света.
Δφ = φ2 – φ1 - разность фаз колебаний в (.) наблюдения.
Если Δφ = const, то это когерентные волны.
Imax при Cos Δφ = 1 Отсюда Δφ = 2∙m∙π - условие max.
Imin при Cos Δφ = 0 Отсюда Δφ = (2∙m+1)π - условие min. - для волн одного направления
и естественного света.
Δφ = φ2 – φ1 - разность фаз колебаний в (.) наблюдения.
Если Δφ = const, то это когерентные волны.
Imax при Cos Δφ = 1 Отсюда Δφ = 2∙m∙π - условие max.
Imin при Cos Δφ = 0 Отсюда Δφ = (2∙m+1)π - условие min.
 
 Оптическая разность хода Оптическая разность хода
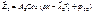

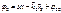
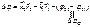
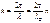 Пусть ΔφО = 0 Пусть ΔφО = 0
Δφ = k2r2 – k1r1
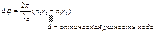  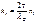
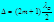  Усл. maxУсл. min Усл. maxУсл. min
| 14. Способы получения интерференционной картины
Для получ. интерфер. от реальных источников можно разделить волну на две части, а потом "сложить" их. Эти половинки – когерентны. Это метод деления волн. Например, в опыте Юнга:
S1 и S2 – вторичные источники
Реальный точечный источник S и экран
 с 2-мя щелями эквивалентен 2-м когер.
Так же работают зеркала и бипризма
Френеля
Интерференционную картину также можно наблюдать при сложении прямой и обратной волн в стоячей волне. И, наконец, интерференция возможна в тонких пленках, например, кольца Ньютона.
Экран с 2-мя щелями эквивалентен 2-м когер.
Так же работают зеркала и бипризма
Френеля
Интерференционную картину также можно наблюдать при сложении прямой и обратной волн в стоячей волне. И, наконец, интерференция возможна в тонких пленках, например, кольца Ньютона.
Экран  1. Рассмотрим подробнее получение
интерференции от 2-х когер. источн. 1. Рассмотрим подробнее получение
интерференции от 2-х когер. источн.
Если среда однородная (по n), то оптическая разность хода:
| 15. Интерференция в тонких пленках. Кольца Ньютона.
 Рассмотр. интерференцию отраженных
1 и 2 лучей, идущих от одного источника. Отражаясь от передней и задней поверх-ти пленки они имеют оптическую разность хода:
Δ12 = (BC + CD)·n – AD·n + λ0/2 Рассмотр. интерференцию отраженных
1 и 2 лучей, идущих от одного источника. Отражаясь от передней и задней поверх-ти пленки они имеют оптическую разность хода:
Δ12 = (BC + CD)·n – AD·n + λ0/2

 Из ΔАDВ и ΔВDС → Из ΔАDВ и ΔВDС →
Усл. max: Усл. min:
В частном случае при θ1 = 0
 Интерференция проходящих лучей тоже есть, но она очень неконтрастна, т.к. интенсивности проходящих лучей резко отличаются друг от друга. Интерференция проходящих лучей тоже есть, но она очень неконтрастна, т.к. интенсивности проходящих лучей резко отличаются друг от друга.
Так I2 ' < I1 ' в 400 раз.
Просветление оптики У стекла коэффициент отражения ρ ≈ 4%.
Для его уменьшения наносят тонкую пленку с коэфф. преломления n'<n.
 Толщина d выбирается такой, чтобы 1 и 2 лучи гасили друг друга. Толщина d выбирается такой, чтобы 1 и 2 лучи гасили друг друга.
Наибольший эффект при Тогда ρ << 4%.
|
16. Временна'я и пространственная когерентность
1) временная
 Здесь φ(t) – случайная фаза.
Когда случайная фаза меняется заметно, волна становится некогерентной сама себе, "забывает" начальную фазу.
Время, за которое это произойдет (Δφ(t) ≈ π) называется
временем когерентности τКОГ.
Расстояние, пройденное волной ℓКОГ = Сф· τКОГ
- длина когерентности.
φ(t) м.б. связана с различными процессами и описываться по-разному.
а) немонохроматичность Здесь φ(t) – случайная фаза.
Когда случайная фаза меняется заметно, волна становится некогерентной сама себе, "забывает" начальную фазу.
Время, за которое это произойдет (Δφ(t) ≈ π) называется
временем когерентности τКОГ.
Расстояние, пройденное волной ℓКОГ = Сф· τКОГ
- длина когерентности.
φ(t) м.б. связана с различными процессами и описываться по-разному.
а) немонохроматичность
 φ(t) = ωt – kr
Δφ = (ω + Δω)t – ωt = Δωt φ(t) = ωt – kr
Δφ = (ω + Δω)t – ωt = Δωt
  б) разброс по k
Δφ = (k + Δk)Z – kZ = ΔkZ т.к. и б) разброс по k
Δφ = (k + Δk)Z – kZ = ΔkZ т.к. и
 в) изменение φ(t) м.б. связана с конечностью длины цуга. в) изменение φ(t) м.б. связана с конечностью длины цуга.
ℓКОГ = ℓЦУГ
Грубая оценка τКОГ для реальных источников ~10-3 с. Для лазеров ~ 10-2 с.
В тонких пленках интерференция возможна при Δ ≤ ℓКОГ
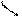
| 17. Многолучевая интерференция
Пусть имеется N колебаний одинаковой амплитуды А0 и одинаковой разности фаз между соседними колебаниями φ. Найдем суммарную амплитуду А.
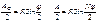  Рассмотрим ΔВОС и ΔBOD: Рассмотрим ΔВОС и ΔBOD:
I ~ A2
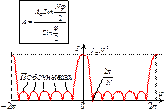
Условие max:φ = 2π∙m (m = 0, ±1, ±2 …) - главные max m-го порядка
 ….. …..
 А = А0NI = N2∙I0 А = А0NI = N2∙I0
  Условие min: Условие min:
(ℓ - целое,
 не кратное N) не кратное N)
Ближайший min - определяет ширину главного max.
| 18. Понятие дифракции. Принцип Гюйгенса-Френеля.
Дифракция изучает поле в областях с резкими неоднородностями среды или в областях с большим скоплением лучей. Здесь законы ГО не применимы.
Дифракция (от лат. diffractus — разломанный) - это явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием. Из-за Д. волны огибают препятствия, проникая в область геометрической тени.
Объяснить явлен. Д. можно на основе принципа Гюйгенса-Френеля:
1. Любую точку волнового фронта можно считать центром вторичного возмущения среды, которое вызывает сферическую волну.
2. Волновой фронт в любой более поздний момент времени – есть огибающая этих вторичных волн.
3. Вторичные волны интерферируют между собой.
Например, после узкой щели в геометрической тени можно наблюдать дифракцию Фраунгофера, а после круглого отверстия – дифракцию Френеля. Для них характерны чередующиеся темные и светлые области на экране.
|
19. Зоны Френеля. Дифракция Френеля на круглом отверстии.
 Разделим сферическую волновую поверхность на бесконечно тонкие кольца.
Любое из колец создает в (.)Р коле-бание с амплитудой δА. Разделим сферическую волновую поверхность на бесконечно тонкие кольца.
Любое из колец создает в (.)Р коле-бание с амплитудой δА.
 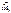  Когда ↑↓ то колебания от 1-го и N-го кольца будут в про-тивофазе, т.е. расстоя-ние до т.Р отличается на λ/2.
Кольца от 1 до N составят 1-ю зону Френеля. Когда ↑↓ то колебания от 1-го и N-го кольца будут в про-тивофазе, т.е. расстоя-ние до т.Р отличается на λ/2.
Кольца от 1 до N составят 1-ю зону Френеля.
Аналогично, когда ↑↓ то расстояние увели-чится еще на λ/2. Это 2-я зона колец.
По амплитуде А1 ≈ А2, но в противофазе. Поэтому суммарная амплитуда от двух соседних зон А≈0.
Такое разбиение на зоны Френеля продолжаем по всей волновой пов-ти. Т.к. расстояние до т.Р с номером зоны растет, то амплитуда зоны АN > AN+1. Поэтому векторная диаграмма для системы зон имеет вид медленно скручивающейся спирали.
   Если волна распространяется в однородной среде без препятствий, то амплитуда в т.Р определяется вектором А∞ Он равен половине амплитуды А1, от 1-й Если волна распространяется в однородной среде без препятствий, то амплитуда в т.Р определяется вектором А∞ Он равен половине амплитуды А1, от 1-й  зоны Френеля. зоны Френеля.
  Найдем радиус m-ой зоны Френеля. Найдем радиус m-ой зоны Френеля.
  a2 = r2m + (a - h)2 = r2m + a2 – 2ah + h2 a2 = r2m + (a - h)2 = r2m + a2 – 2ah + h2
r2m = 2ah (*)
|  20. Дифракция Фраунгофера на щели 20. Дифракция Фраунгофера на щели
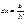 Разобьем щель на N узких полос
шириной. θ – угол дифракции.
В (.)Р колебание – результат интерференции
от всех N полос.
δА – амплитуда от одной полосы.
Из многолучевой интерференции мы знаем, что Разобьем щель на N узких полос
шириной. θ – угол дифракции.
В (.)Р колебание – результат интерференции
от всех N полос.
δА – амплитуда от одной полосы.
Из многолучевой интерференции мы знаем, что
Разность хода лучей от соседних  вторичных источников dΔ = dx∙Sinθ вторичных источников dΔ = dx∙Sinθ
Разность фаз
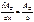
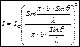
- зависимость интенсив-ти от угла дифракции
Условие min:
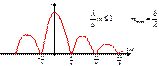
| 21. Дифракция Фраунгофера на дифракционной решетке.
 Дифр. решетка – это периодическая структура с чередующимися щелями на непрозрачном экране. На 1 мм 50…1000 щелей.
d – период решетки
b – ширина щели
N – число щелей
Δ – разность хода
θ – угол дифракции
(играет роль координаты)
Чтобы найти амплитуду колебаний в т.Р, надо сложить N колебаний ≈ одинаковой амплитуды А1 и с одинаковым сдвигом фазы Δφ колебаний от соседних щелей. Дифр. решетка – это периодическая структура с чередующимися щелями на непрозрачном экране. На 1 мм 50…1000 щелей.
d – период решетки
b – ширина щели
N – число щелей
Δ – разность хода
θ – угол дифракции
(играет роль координаты)
Чтобы найти амплитуду колебаний в т.Р, надо сложить N колебаний ≈ одинаковой амплитуды А1 и с одинаковым сдвигом фазы Δφ колебаний от соседних щелей.
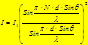 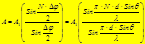
Здесь А0 и I0 – ампл-да и интенсивность колебания в центре дифракционной картины, т.е. при θ = 0.
|
22. Дифракционная решетка как спектральный прибор.
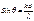 - зависит от λ. Следовательно, немонохроматичный
свет разложится в спектр.
- зависит от λ. Следовательно, немонохроматичный
свет разложится в спектр.
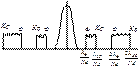 Спектральный прибор характеризуется дисперсией: Спектральный прибор характеризуется дисперсией:
- угловой
- линейной
δθ – угловое расстояние между гл. max спектральн. компонент, отличающихся на δλ.
δℓ - линейное ---"---.
 Угловая дисперсия Угловая дисперсия
d·Sinθ = kλ d·Cosθ·δθ = k·δλ
Линейная дисперсия
 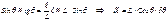
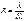 Разрешающая способность дифр. решетки, как и любого спектра-льного прибора, определяет минимальную разность длин волн δλ, при которой главные максимумы для волн λ и λ+δλ воспринимаются в спектре раздельно. Разрешающей способностью называют безразмерную величину Разрешающая способность дифр. решетки, как и любого спектра-льного прибора, определяет минимальную разность длин волн δλ, при которой главные максимумы для волн λ и λ+δλ воспринимаются в спектре раздельно. Разрешающей способностью называют безразмерную величину
Критерий Рэлея:
 т.е. разр. способность выше у решетки т.е. разр. способность выше у решетки
с большим N и в max высших порядков k
|  23. Дисперсия. Дисперсионное соотношение. Групповая и фазовая скорости.
В однородных изотропных средах без дисперсии 23. Дисперсия. Дисперсионное соотношение. Групповая и фазовая скорости.
В однородных изотропных средах без дисперсии
  С учетом дисперсии: С учетом дисперсии:
Здесь - функции влияния.
Зависимость D от Е во всех точках пространства – пространственная дисперсия.
 Зависимость D от Е во всех предшествующих моментах времени – временная дисперсия. Зависимость D от Е во всех предшествующих моментах времени – временная дисперсия.
Для монохроматичной волны:
 - временная дисперсия; - временная дисперсия;
 - пространственная дисперсия; - пространственная дисперсия;
 - временная и пространственная. - временная и пространственная.
 - дисперсионное соотношение - дисперсионное соотношение
определяет связь
 Если дисперсии нет, то Если дисперсии нет, то
и связь - линейная.
       С дисперсией: С дисперсией:

Дисперсия вещества – величина
- нормальная дисперсия;
- аномальная.
| 24. Элементарная теория дисперсии
 Рассмотрим атом, состоящий из + протона и – электрона. Рассмотрим атом, состоящий из + протона и – электрона.
  - осциллятор; - собственная частота осциллятора. - осциллятор; - собственная частота осциллятора.
Если нет внешнего поля: - ур-ие колебаний
 Если есть поле, то Если есть поле, то
 Сила Лоренца Сила Лоренца
 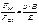 B = μμoH В волне тогда B = μμoH В волне тогда
ССР – скорость света
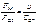 в среде в среде
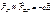  Пусть тогда FM << FЭЛ и Пусть тогда FM << FЭЛ и
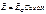  Тогда уравнение осциллятора Тогда уравнение осциллятора
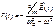  В точке нахождения атома Тогда В точке нахождения атома Тогда
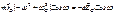
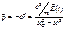
Дипольный момент атома
  В молекуле (у каждого осциллятора своя ω0) В молекуле (у каждого осциллятора своя ω0)
Дипольный момент молекулы:
Поляризация ΔN – кол-во молекул в ΔV
 n0 – концентрация молекул n0 – концентрация молекул
χ – диэлектрическая восприимчивость.
|
Кольца Ньютона(в отраженном свете)
 Плоско-выпуклая линза большого радиуса кривизны (R~ 1 м) на стекля-ном зеркале.
Лучи падают нормально к повер-ти.
Роль тонкой пленки играет воздушный зазор толщины b.
Луч 1 отраж. в т.А, луч 2 – в т.В.
Наблюдаем концентрические темные и светлые кольца равной толщины.
Угол падения на сферическую поверхность очень мал, поэтому отраженные лучи 1 и 2 идут почти вертикально. Плоско-выпуклая линза большого радиуса кривизны (R~ 1 м) на стекля-ном зеркале.
Лучи падают нормально к повер-ти.
Роль тонкой пленки играет воздушный зазор толщины b.
Луч 1 отраж. в т.А, луч 2 – в т.В.
Наблюдаем концентрические темные и светлые кольца равной толщины.
Угол падения на сферическую поверхность очень мал, поэтому отраженные лучи 1 и 2 идут почти вертикально.
  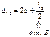 Усл. max:
Усл. max:
  Усл. min:
Усл. min:
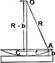 Из ΔАОС:
R2 = r2 + (R-b)2 r2 ≈ 2bR
Тогда
Условие светлых колец: Условие темных колец:
Из ΔАОС:
R2 = r2 + (R-b)2 r2 ≈ 2bR
Тогда
Условие светлых колец: Условие темных колец:
Кольца Ньютона (в проходящем свете)

Здесь условия для светлых и темных колец меняются местами.
| 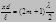  Условия max и min:
max: min: Условия max и min:
max: min:
 - ширина интерференционной полосы
2. Стоячая волна Для падающей волны:
- ширина интерференционной полосы
2. Стоячая волна Для падающей волны:
Для отраженной:
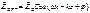
 При Z = 0 (из усл. непрерывности Еτ на границе) Еτ = 0. При Z = 0 (из усл. непрерывности Еτ на границе) Еτ = 0.
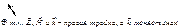
 В стоячей волне вектора Е и Н колеблются в противофазе, В стоячей волне вектора Е и Н колеблются в противофазе,
а в бегущей – в фазе.
 Вектор Умова-Пойтинга: Вектор Умова-Пойтинга:
- в стоячей волне энергия не переносится.
|
|
|
|
|
2) пространственная когерентность
Нарушение когерентности м.б. связано с конечностью размеров источников света.
 Интерференционные полосы перестанут различаться, если max от одной границы щели наложится на min от другой границы. Интерференционные полосы перестанут различаться, если max от одной границы щели наложится на min от другой границы.
~
где φ – угловой размер источника.
|
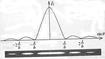
  Если разность хода от соседних щелей Δ = kλ, то колебания от разных щелей приходят в т.Р в одной фазе и складываются (т.е. усиливаются). Это главные максимумы. Здесь k = 0, ±1, ±2… - порядок главного max. Если разность хода от соседних щелей Δ = kλ, то колебания от разных щелей приходят в т.Р в одной фазе и складываются (т.е. усиливаются). Это главные максимумы. Здесь k = 0, ±1, ±2… - порядок главного max.
 Координаты минимумов найдем из условия
Координаты минимумов найдем из условия
 Ближайший к нулевому max минимум, определяющий ширину главных max:
Условие применимости приближения Фраунгофера
Лучи можно считать параллель-ными, если
Δ1 – Δ2 << λ
d(Sinθ1 – Sinθ2) << λ Ближайший к нулевому max минимум, определяющий ширину главных max:
Условие применимости приближения Фраунгофера
Лучи можно считать параллель-ными, если
Δ1 – Δ2 << λ
d(Sinθ1 – Sinθ2) << λ
 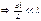
ℓ = d·N
ℓ = d·N

| Различие дифракции Френеля и Фраунгофера.
Дифракция Френеля – это более общий случай, а у Фраунгофера – частный, когда лучи можно считать параллельными. Часто дифракцию Фраунгофера называют "дифракцией в параллельных лучах".
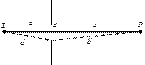 Лучи можно считать параллельными, если
b' - b << λ Лучи можно считать параллельными, если
b' - b << λ
Аналогично a' – a << λ и
Это условия применимости приближений Фраунгофера.
Если - дифракция Фраунгофера, если - Френеля,
если - законы геометрической оптики (ГО).
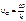
|    
2bh + r2m = bmλ Тогда с учетом (*) получим:
|
Поиск по сайту:
|

 I – интенсивность света – средняя по времени энергия, переносимая э-м волной через ед. площадку, ┴ к направлению распространения волны в единицу t. Для света. где S –вектор Умова-Пойтинга
I – интенсивность света – средняя по времени энергия, переносимая э-м волной через ед. площадку, ┴ к направлению распространения волны в единицу t. Для света. где S –вектор Умова-Пойтинга


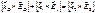


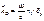

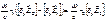
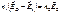
 Из (1) и (2) имеем (при y=0):
Из (1) и (2) имеем (при y=0):
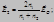
 При отражении от оптически более плотной среды происходит изменение фазы на π.
При отражении от оптически более плотной среды происходит изменение фазы на π.
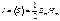





 2) Тогда и
2) Тогда и

 I = I1 + I2 (независимо от Δφ)
I = I1 + I2 (независимо от Δφ)


 Интерференция – сложение колебаний, при котором происходит перераспределение энергии светового потока и могут наблюдаться минимумы и максимумы интенсивности.
Интерференция – сложение колебаний, при котором происходит перераспределение энергии светового потока и могут наблюдаться минимумы и максимумы интенсивности.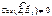 Наблюдается при зависимости фаз колебаний (т.е. CosΔφ ≠ 0) и не-перпендикулярности векторов Е (т.е.).
Наблюдается при зависимости фаз колебаний (т.е. CosΔφ ≠ 0) и не-перпендикулярности векторов Е (т.е.). Принцип действия
Принцип действия
 П. свободно пропускает колебания с вектором, лежащим в одной плоскости, называемой пл. поляризатора (ПП).
П. свободно пропускает колебания с вектором, лежащим в одной плоскости, называемой пл. поляризатора (ПП).

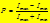 Если пл. колебаний вектора лежит в ПП, то волна проходит полностью. Если пл. колебаний ПП, то волна не проходит. В остальных случаях волна проходит частично.
- степень поляризации, где Imax и Imin - макс и мин
возможные интенсивности.
0 ≤Р≤ 1 Р = 0 – естественный свет; Р = 1 – плоскополяризованный свет.
Закон Малюса (для плоскополяриз. света)
Пусть на идеал. П. падает плоскополяр. свет и угол между пл. колебаний падающего света и ПП = φ.
Тогда интенсивность света на выходе IВЫХ = IВХ∙Сos2φ
Если пл. колебаний вектора лежит в ПП, то волна проходит полностью. Если пл. колебаний ПП, то волна не проходит. В остальных случаях волна проходит частично.
- степень поляризации, где Imax и Imin - макс и мин
возможные интенсивности.
0 ≤Р≤ 1 Р = 0 – естественный свет; Р = 1 – плоскополяризованный свет.
Закон Малюса (для плоскополяриз. света)
Пусть на идеал. П. падает плоскополяр. свет и угол между пл. колебаний падающего света и ПП = φ.
Тогда интенсивность света на выходе IВЫХ = IВХ∙Сos2φ
 - для волн одного направления
и естественного света.
Δφ = φ2 – φ1 - разность фаз колебаний в (.) наблюдения.
Если Δφ = const, то это когерентные волны.
Imax при Cos Δφ = 1 Отсюда Δφ = 2∙m∙π - условие max.
Imin при Cos Δφ = 0 Отсюда Δφ = (2∙m+1)π - условие min.
- для волн одного направления
и естественного света.
Δφ = φ2 – φ1 - разность фаз колебаний в (.) наблюдения.
Если Δφ = const, то это когерентные волны.
Imax при Cos Δφ = 1 Отсюда Δφ = 2∙m∙π - условие max.
Imin при Cos Δφ = 0 Отсюда Δφ = (2∙m+1)π - условие min.


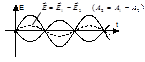
 Оптическая разность хода
Оптическая разность хода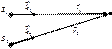
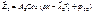

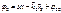
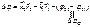
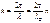 Пусть ΔφО = 0
Пусть ΔφО = 0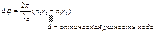

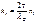
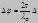
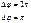

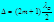
 Усл. maxУсл. min
Усл. maxУсл. min с 2-мя щелями эквивалентен 2-м когер.
Так же работают зеркала и бипризма
Френеля
Интерференционную картину также можно наблюдать при сложении прямой и обратной волн в стоячей волне. И, наконец, интерференция возможна в тонких пленках, например, кольца Ньютона.
Экран
с 2-мя щелями эквивалентен 2-м когер.
Так же работают зеркала и бипризма
Френеля
Интерференционную картину также можно наблюдать при сложении прямой и обратной волн в стоячей волне. И, наконец, интерференция возможна в тонких пленках, например, кольца Ньютона.
Экран  1. Рассмотрим подробнее получение
интерференции от 2-х когер. источн.
1. Рассмотрим подробнее получение
интерференции от 2-х когер. источн.



 Рассмотр. интерференцию отраженных
1 и 2 лучей, идущих от одного источника. Отражаясь от передней и задней поверх-ти пленки они имеют оптическую разность хода:
Δ12 = (BC + CD)·n – AD·n + λ0/2
Рассмотр. интерференцию отраженных
1 и 2 лучей, идущих от одного источника. Отражаясь от передней и задней поверх-ти пленки они имеют оптическую разность хода:
Δ12 = (BC + CD)·n – AD·n + λ0/2

 Из ΔАDВ и ΔВDС →
Из ΔАDВ и ΔВDС →



 Интерференция проходящих лучей тоже есть, но она очень неконтрастна, т.к. интенсивности проходящих лучей резко отличаются друг от друга.
Интерференция проходящих лучей тоже есть, но она очень неконтрастна, т.к. интенсивности проходящих лучей резко отличаются друг от друга. Толщина d выбирается такой, чтобы 1 и 2 лучи гасили друг друга.
Толщина d выбирается такой, чтобы 1 и 2 лучи гасили друг друга. Здесь φ(t) – случайная фаза.
Когда случайная фаза меняется заметно, волна становится некогерентной сама себе, "забывает" начальную фазу.
Время, за которое это произойдет (Δφ(t) ≈ π) называется
временем когерентности τКОГ.
Расстояние, пройденное волной ℓКОГ = Сф· τКОГ
- длина когерентности.
φ(t) м.б. связана с различными процессами и описываться по-разному.
а) немонохроматичность
Здесь φ(t) – случайная фаза.
Когда случайная фаза меняется заметно, волна становится некогерентной сама себе, "забывает" начальную фазу.
Время, за которое это произойдет (Δφ(t) ≈ π) называется
временем когерентности τКОГ.
Расстояние, пройденное волной ℓКОГ = Сф· τКОГ
- длина когерентности.
φ(t) м.б. связана с различными процессами и описываться по-разному.
а) немонохроматичность
 φ(t) = ωt – kr
Δφ = (ω + Δω)t – ωt = Δωt
φ(t) = ωt – kr
Δφ = (ω + Δω)t – ωt = Δωt

 б) разброс по k
Δφ = (k + Δk)Z – kZ = ΔkZ т.к. и
б) разброс по k
Δφ = (k + Δk)Z – kZ = ΔkZ т.к. и

 в) изменение φ(t) м.б. связана с конечностью длины цуга.
в) изменение φ(t) м.б. связана с конечностью длины цуга.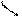
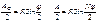
 Рассмотрим ΔВОС и ΔBOD:
Рассмотрим ΔВОС и ΔBOD:


 …..
….. А = А0NI = N2∙I0
А = А0NI = N2∙I0
 Условие min:
Условие min: не кратное N)
не кратное N) Разделим сферическую волновую поверхность на бесконечно тонкие кольца.
Любое из колец создает в (.)Р коле-бание с амплитудой δА.
Разделим сферическую волновую поверхность на бесконечно тонкие кольца.
Любое из колец создает в (.)Р коле-бание с амплитудой δА.

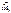
 Когда ↑↓ то колебания от 1-го и N-го кольца будут в про-тивофазе, т.е. расстоя-ние до т.Р отличается на λ/2.
Кольца от 1 до N составят 1-ю зону Френеля.
Когда ↑↓ то колебания от 1-го и N-го кольца будут в про-тивофазе, т.е. расстоя-ние до т.Р отличается на λ/2.
Кольца от 1 до N составят 1-ю зону Френеля.

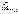


 Если волна распространяется в однородной среде без препятствий, то амплитуда в т.Р определяется вектором А∞ Он равен половине амплитуды А1, от 1-й
Если волна распространяется в однородной среде без препятствий, то амплитуда в т.Р определяется вектором А∞ Он равен половине амплитуды А1, от 1-й  зоны Френеля.
зоны Френеля.
 Найдем радиус m-ой зоны Френеля.
Найдем радиус m-ой зоны Френеля.
 a2 = r2m + (a - h)2 = r2m + a2 – 2ah + h2
a2 = r2m + (a - h)2 = r2m + a2 – 2ah + h2 20. Дифракция Фраунгофера на щели
20. Дифракция Фраунгофера на щели
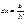 Разобьем щель на N узких полос
шириной. θ – угол дифракции.
В (.)Р колебание – результат интерференции
от всех N полос.
δА – амплитуда от одной полосы.
Из многолучевой интерференции мы знаем, что
Разобьем щель на N узких полос
шириной. θ – угол дифракции.
В (.)Р колебание – результат интерференции
от всех N полос.
δА – амплитуда от одной полосы.
Из многолучевой интерференции мы знаем, что


 вторичных источников dΔ = dx∙Sinθ
вторичных источников dΔ = dx∙Sinθ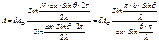
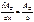
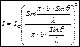



 Дифр. решетка – это периодическая структура с чередующимися щелями на непрозрачном экране. На 1 мм 50…1000 щелей.
d – период решетки
b – ширина щели
N – число щелей
Δ – разность хода
θ – угол дифракции
(играет роль координаты)
Чтобы найти амплитуду колебаний в т.Р, надо сложить N колебаний ≈ одинаковой амплитуды А1 и с одинаковым сдвигом фазы Δφ колебаний от соседних щелей.
Дифр. решетка – это периодическая структура с чередующимися щелями на непрозрачном экране. На 1 мм 50…1000 щелей.
d – период решетки
b – ширина щели
N – число щелей
Δ – разность хода
θ – угол дифракции
(играет роль координаты)
Чтобы найти амплитуду колебаний в т.Р, надо сложить N колебаний ≈ одинаковой амплитуды А1 и с одинаковым сдвигом фазы Δφ колебаний от соседних щелей.

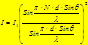
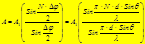


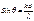 - зависит от λ. Следовательно, немонохроматичный
свет разложится в спектр.
- зависит от λ. Следовательно, немонохроматичный
свет разложится в спектр.
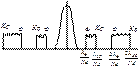 Спектральный прибор характеризуется дисперсией:
Спектральный прибор характеризуется дисперсией:


 Угловая дисперсия
Угловая дисперсия
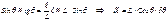
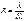 Разрешающая способность дифр. решетки, как и любого спектра-льного прибора, определяет минимальную разность длин волн δλ, при которой главные максимумы для волн λ и λ+δλ воспринимаются в спектре раздельно. Разрешающей способностью называют безразмерную величину
Разрешающая способность дифр. решетки, как и любого спектра-льного прибора, определяет минимальную разность длин волн δλ, при которой главные максимумы для волн λ и λ+δλ воспринимаются в спектре раздельно. Разрешающей способностью называют безразмерную величину т.е. разр. способность выше у решетки
т.е. разр. способность выше у решетки 23. Дисперсия. Дисперсионное соотношение. Групповая и фазовая скорости.
В однородных изотропных средах без дисперсии
23. Дисперсия. Дисперсионное соотношение. Групповая и фазовая скорости.
В однородных изотропных средах без дисперсии

 С учетом дисперсии:
С учетом дисперсии:

 Зависимость D от Е во всех предшествующих моментах времени – временная дисперсия.
Зависимость D от Е во всех предшествующих моментах времени – временная дисперсия. - временная дисперсия;
- временная дисперсия; - пространственная дисперсия;
- пространственная дисперсия; - временная и пространственная.
- временная и пространственная.
 - дисперсионное соотношение
- дисперсионное соотношение





 С дисперсией:
С дисперсией:







 Рассмотрим атом, состоящий из + протона и – электрона.
Рассмотрим атом, состоящий из + протона и – электрона.

 - осциллятор; - собственная частота осциллятора.
- осциллятор; - собственная частота осциллятора.
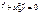
 Если есть поле, то
Если есть поле, то Сила Лоренца
Сила Лоренца
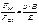 B = μμoH В волне тогда
B = μμoH В волне тогда
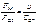 в среде
в среде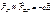
 Пусть тогда FM << FЭЛ и
Пусть тогда FM << FЭЛ и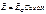
 Тогда уравнение осциллятора
Тогда уравнение осциллятора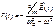
 В точке нахождения атома Тогда
В точке нахождения атома Тогда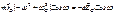
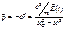

 В молекуле (у каждого осциллятора своя ω0)
В молекуле (у каждого осциллятора своя ω0)
 n0 – концентрация молекул
n0 – концентрация молекул Плоско-выпуклая линза большого радиуса кривизны (R~ 1 м) на стекля-ном зеркале.
Лучи падают нормально к повер-ти.
Роль тонкой пленки играет воздушный зазор толщины b.
Луч 1 отраж. в т.А, луч 2 – в т.В.
Наблюдаем концентрические темные и светлые кольца равной толщины.
Угол падения на сферическую поверхность очень мал, поэтому отраженные лучи 1 и 2 идут почти вертикально.
Плоско-выпуклая линза большого радиуса кривизны (R~ 1 м) на стекля-ном зеркале.
Лучи падают нормально к повер-ти.
Роль тонкой пленки играет воздушный зазор толщины b.
Луч 1 отраж. в т.А, луч 2 – в т.В.
Наблюдаем концентрические темные и светлые кольца равной толщины.
Угол падения на сферическую поверхность очень мал, поэтому отраженные лучи 1 и 2 идут почти вертикально.


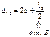 Усл. max:
Усл. max:

 Усл. min:
Усл. min:
 Из ΔАОС:
R2 = r2 + (R-b)2 r2 ≈ 2bR
Тогда
Условие светлых колец: Условие темных колец:
Из ΔАОС:
R2 = r2 + (R-b)2 r2 ≈ 2bR
Тогда
Условие светлых колец: Условие темных колец:




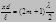
 Условия max и min:
max: min:
Условия max и min:
max: min:
 - ширина интерференционной полосы
2. Стоячая волна Для падающей волны:
- ширина интерференционной полосы
2. Стоячая волна Для падающей волны:

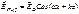
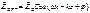
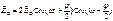

 При Z = 0 (из усл. непрерывности Еτ на границе) Еτ = 0.
При Z = 0 (из усл. непрерывности Еτ на границе) Еτ = 0.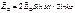
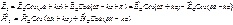
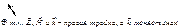
 В стоячей волне вектора Е и Н колеблются в противофазе,
В стоячей волне вектора Е и Н колеблются в противофазе, Вектор Умова-Пойтинга:
Вектор Умова-Пойтинга:

 Интерференционные полосы перестанут различаться, если max от одной границы щели наложится на min от другой границы.
Интерференционные полосы перестанут различаться, если max от одной границы щели наложится на min от другой границы.




 Если разность хода от соседних щелей Δ = kλ, то колебания от разных щелей приходят в т.Р в одной фазе и складываются (т.е. усиливаются). Это главные максимумы. Здесь k = 0, ±1, ±2… - порядок главного max.
Если разность хода от соседних щелей Δ = kλ, то колебания от разных щелей приходят в т.Р в одной фазе и складываются (т.е. усиливаются). Это главные максимумы. Здесь k = 0, ±1, ±2… - порядок главного max.
 Координаты минимумов найдем из условия
Координаты минимумов найдем из условия
 Ближайший к нулевому max минимум, определяющий ширину главных max:
Условие применимости приближения Фраунгофера
Лучи можно считать параллель-ными, если
Δ1 – Δ2 << λ
d(Sinθ1 – Sinθ2) << λ
Ближайший к нулевому max минимум, определяющий ширину главных max:
Условие применимости приближения Фраунгофера
Лучи можно считать параллель-ными, если
Δ1 – Δ2 << λ
d(Sinθ1 – Sinθ2) << λ
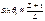


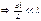



 Лучи можно считать параллельными, если
b' - b << λ
Лучи можно считать параллельными, если
b' - b << λ