Численные методы
Тема: «Решение уравнений с одним неизвестным»
1. Методом дихотомии найти корни уравнения 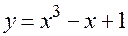
Решение. Вычислим несколько значений функции 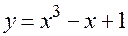 :
:  ;
;  ;
; 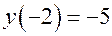 . Значит один корень этого уравнения лежит в промежутке
. Значит один корень этого уравнения лежит в промежутке  . Для нахождения локальных экстремумов, приравняем нулю производную
. Для нахождения локальных экстремумов, приравняем нулю производную  . То есть в точках
. То есть в точках 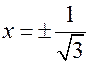 у функции
у функции 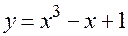 имеются экстремумы. Найдём
имеются экстремумы. Найдём  : Теперь найдём
: Теперь найдём
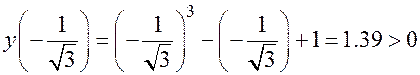 . Отсюда видно, что у функции
. Отсюда видно, что у функции 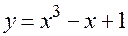 один действительный корень, и лежит он в промежутке
один действительный корень, и лежит он в промежутке  . Найдём его методом дихотомии, имеем:
. Найдём его методом дихотомии, имеем:

| -2 | -1.5 | -1.375 | -1.34 | -1.33 | -1.325 | -1.32 | -1.312 | -1.25 | -1 |

| -5 | -0.875 | -0.225 | -0.11 | -0.003 | -0.001 | 0.013 | 0.0515 | 0.297 |
Итак, методом дихотомии найден корень уравнения 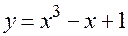 равный
равный  .
.
Точность найденного корня определим по формуле
 . В нашей задаче:
. В нашей задаче: 
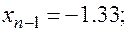
 Отсюда
Отсюда 
Ответ. Корень уравнения 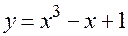 :
:  , точность:
, точность:  .
.
2. Методом дихотомии найти корни уравнения 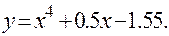
Решение. Вычислим несколько значений функции  :
:  ;
;  ;
; 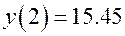 .
.  ;
;  . Значит один корень этого уравнения лежит в промежутке
. Значит один корень этого уравнения лежит в промежутке  , второй – в промежутке
, второй – в промежутке  .
.
Найдём первый корень методом дихотомии, имеем:

| 1.008 | 1.0115 | 1.015 | 1.03 | 1.0625 | 1.125 | 1.25 | 1.5 | ||

| -1.05 | -0.014 | 0.003 | 0.02 | 0.1 | 0.26 | 0.611 | 1.52 | 4.26 | 15.45 |
Методом дихотомии найден первый корень уравнения  равный
равный  .
.
Точность найденного корня определим по формуле  . В нашей задаче:
. В нашей задаче: 
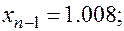
 Отсюда
Отсюда 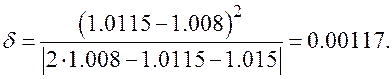
Найдём второй корень методом дихотомии, имеем:

| -2 | -1.5 | -1.25 | -1.22 | -1.2 | -1.1875 | -1.125 | -1 |

| 13.45 | 2.76 | 0.265 | 0.105 | -0.08 | -0.154 | -0.51 | -1.05 |
Методом дихотомии найден второй корень уравнения  , равный
, равный 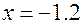 .
.
Точность найденного корня определим по формуле  . В нашей задаче:
. В нашей задаче: 
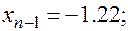
 Отсюда
Отсюда 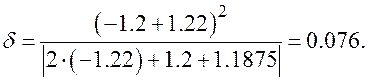
Ответ. Корни уравнения  :
:  , точность
, точность  ;
;  , точность
, точность 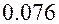 .
.
_____________________________________________________________
3. Методом дихотомии найти корни уравнения 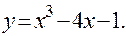 Решение. Вычислим несколько значений функции
Решение. Вычислим несколько значений функции 
 ,
,  ,
, 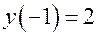 ,
,  ,
,  ,
, 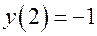 ,
,  . Значит один корень уравнения
. Значит один корень уравнения 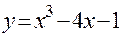 лежит в промежутке
лежит в промежутке  , второй – в промежутке
, второй – в промежутке  , и третий корень лежит в промежутке
, и третий корень лежит в промежутке  .
.
Найдём первый корень методом дихотомии, имеем:

| -2 | -1.875 | -1.86 | -1.84 | -1.8125 | -1.75 | -1.5 | -1 |

| -1 | -0.09 | 0.005 | 0.1 | 0.3 | 0.6 | 1.6 |
Методом дихотомии найден первый корень уравнения 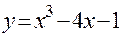 , равный
, равный 
Точность найденного корня определим по формуле 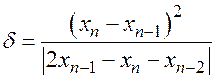 . В нашей задаче:
. В нашей задаче: 
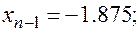
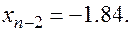 Отсюда
Отсюда 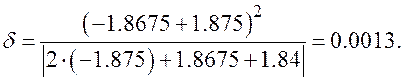
Найдём второй корень методом дихотомии, имеем:

| -1 | -0.3125 | -0.28 | -0.266 | -0.258 | -0.25 | |

| 0.219 | 0.102 | 0.045 | 0.0004 | -0.016 | -1 |
Методом дихотомии найден второй корень уравнения 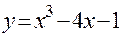 , равный
, равный 
Точность найденного корня определим по формуле 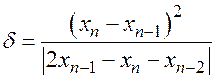 . В нашей задаче:
. В нашей задаче: 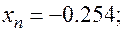
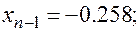
 Отсюда
Отсюда 
Найдём третий корень методом дихотомии, имеем:

| 2.0625 | 2.09 | 2.1 | 2.11 | 2.115 | 2.12 | 2. 125 | 2.25 | 2.5 | ||

| -1 | -0.5 | -0.2 | -0.07 | -0.02 | 0.0009 | 0.05 | 0.1 | 1.39 | 2.6 |
Методом дихотомии найден третий корень уравнения 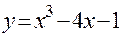 , равный
, равный 
Точность найденного корня определим по формуле 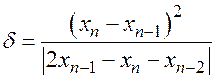 . В нашей задаче:
. В нашей задаче: 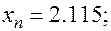

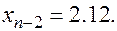 Отсюда
Отсюда 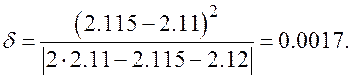
Ответ. Корни уравнения 
 , точность
, точность 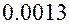 ;
;  , точность
, точность  ,
, 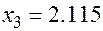 , точность
, точность 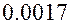 .
.
_____________________________________________________________
4. Используя найденные графическим путём начальные приближения, способом простых итераций вычислить с точностью до 0.01 действительные корни уравнения 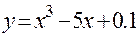 .
.
Решение. Для преобразования уравнения  к виду
к виду
 заменяем уравнение
заменяем уравнение  эквивалентным ему уравнением
эквивалентным ему уравнением  где число
где число  выбирается так, чтобы функция
выбирается так, чтобы функция  была малой по абсолютной величине в окрестности точки
была малой по абсолютной величине в окрестности точки 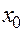 (например, можно положить
(например, можно положить 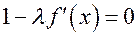 ). Построив график функции
). Построив график функции 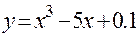 , видим, что корни данной функции находятся вблизи точек 0, +2 и -2. Имеем:
, видим, что корни данной функции находятся вблизи точек 0, +2 и -2. Имеем: 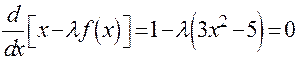 .
.
4.1. Полагаем  т.е. будем вначале искать корень вблизи точки 0:
т.е. будем вначале искать корень вблизи точки 0:  . Отсюда
. Отсюда 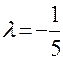 . Значит итерационный процесс
. Значит итерационный процесс  будет выглядеть так:
будет выглядеть так:  . Итерируем:
. Итерируем: 
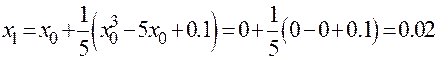 ,
,
 .
.
Итак, один корень найден. Он равен 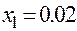 .
.
4.2. Полагаем  т.е. будем искать корень вблизи точки 2:
т.е. будем искать корень вблизи точки 2:  . Отсюда
. Отсюда 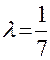 . Значит итерационный процесс
. Значит итерационный процесс  будет выглядеть так:
будет выглядеть так:
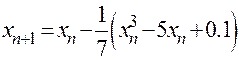 . Итерируем:
. Итерируем: 
 ,
,
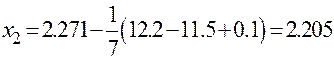 ,
,
 ,
,
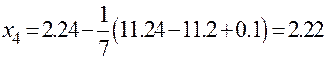 ,
,
 .
.
Значит, второй корень уравнения будет равен 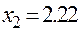 .
.
4.3. Полагаем  т.е. будем искать корень вблизи точки -2:
т.е. будем искать корень вблизи точки -2:  . Отсюда
. Отсюда  . Значит итерационный процесс
. Значит итерационный процесс 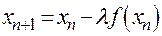 будет выглядеть так:
будет выглядеть так:
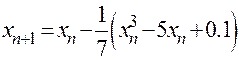 . Итерируем:
. Итерируем: 
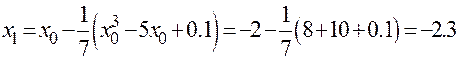 ,
,
 ,
,
 ,
,
 .,
.,
 .
.
Таким образом, третий корень уравнения будет равен  .
.
Ответ. 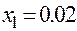 ,
, 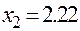 ,
, 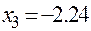 .
.
_____________________________________________________________
5. Используя найденные графическим путём начальные приближения, способом простых итераций вычислить с точностью до 0.01 действительные корни уравнения 
Решение. Для преобразования уравнения 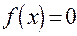 к виду
к виду
 заменяем уравнение
заменяем уравнение 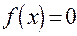 эквивалентным ему уравнением
эквивалентным ему уравнением  где число
где число  выбирается так, чтобы функция
выбирается так, чтобы функция  была малой по абсолютной величине в окрестности точки
была малой по абсолютной величине в окрестности точки  (например, можно положить
(например, можно положить 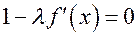 ). Построив график функции
). Построив график функции  видим, что корень данной функции находится в промежутке
видим, что корень данной функции находится в промежутке  . Имеем:
. Имеем:  .
.
Полагаем  т.е. будем искать корень вблизи точки 1.5:
т.е. будем искать корень вблизи точки 1.5: 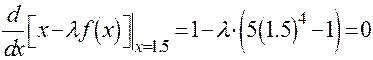 . Отсюда
. Отсюда 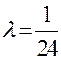 . Значит итерационный процесс
. Значит итерационный процесс 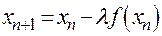 будет выглядеть так:
будет выглядеть так:  . Итерируем:
. Итерируем: 
 ,
,
 .
.


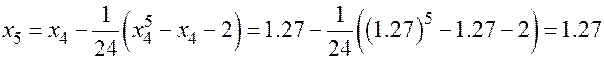
Ответ.  .
.
__________________________________________________________ Домашнее задание. Методами дихотомии и простых итераций найти корни уравнений
1. 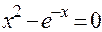 .
.
2.  .
.