Работа обязательно должна содержать титульный лист с указанием на нем фамилии и полного имени студента. Данные каждого варианта определяется параметрами p1 и p2. При выполнении контрольных заданий студент должен подставить там, где это необходимо, вместо буквенных параметров индивидуальные анкетные характеристики: p1– число букв в полном имени студента; p1 – число букв в фамилии студента.
Задача 1. Известны данные по территориям региона
(p1 – число букв в полном имени, p2 – число букв в фамилии):
Таблица 1 – Исходные данные для задачи 1

Требуется:
1. Построить линейное уравнение парной регрессии y по x.
2. Рассчитать линейный коэффициент парной корреляции, коэффициент детерминации и среднюю ошибку аппроксимации.
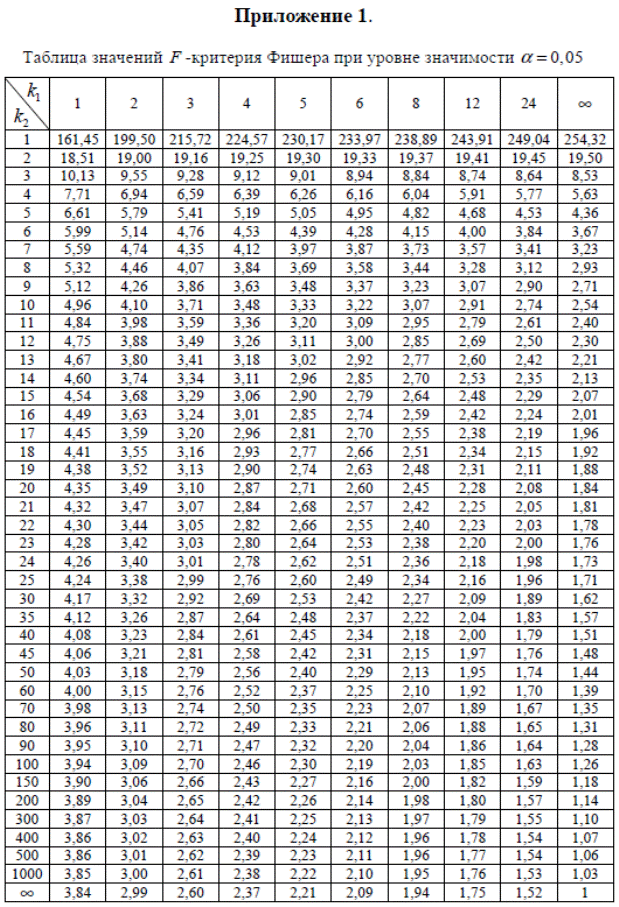
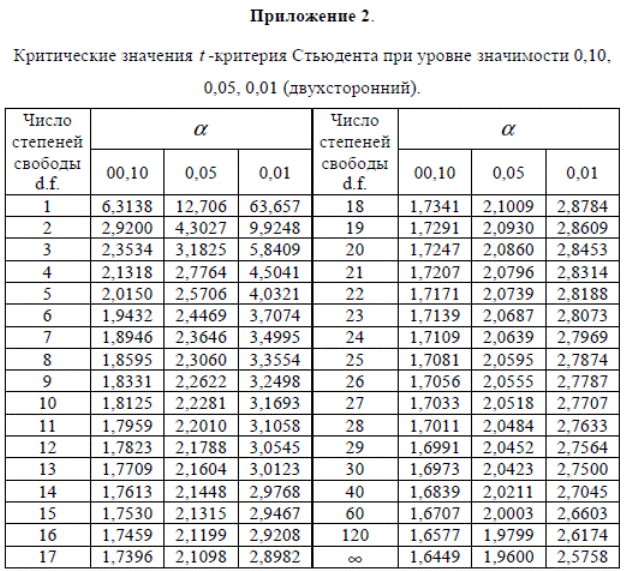
3. Оценить статистическую значимость уравнения регрессии в целом и отдельных параметров регрессии и корреляции с помощью F -критерия Фишера и t -критерия Стьюдента.
4. Выполнить прогноз заработной платы y при прогнозном значении среднедушевого прожиточного минимума x, составляющем 107% от среднего уровня.
5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.
6. На одном графике отложить исходные данные и теоретическую прямую.
7. Проверить вычисления в MS Excel.
Задача 2. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов x1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих x2 (%) (p1 – число букв в полном имени, p2 – число букв в фамилии):
Таблица 2 – Исходные данные для задачи 2

Требуется:
1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
4. С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации.
5. С помощью t-критерия Стьюдента оценить статистическую значимость параметров чистой регрессии.
6. С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 и фактора x2 после x1.
7. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
8. Проверить вычисления в MS Excel.
Задача 3.
Имеются данные о значениях показателей
X1-среднедушевой доход (ден. ед.) и
Y –расходы на потребление (ден. ед.)
Они внесены в таблицу 3.
Таблица 3 – Данные о среднедушевых доходах и расходах на потребление
| Вариант 1.1 | Вариант 1.2 | Вариант 1.3 | Вариант 1.4 | Вариант 1.5 | |||||
| Х1 | у | Х1 | у | Х1 | у | Х1 | у | Х1 | у |
| Вариант 1.6 | Вариант 1.7 | Вариант 1.8 | Вариант 1.9 | Вариант 1.10 | |||||
| Х1 | у | Х1 | у | Х1 | у | Х1 | у | Х1 | у |
Требуется:
1) построить графическую модель спроса – функцию зависимости спроса от дохода в виде точечной диаграммы средствами MS Excel
2) изучить форму связи между доходом и потреблением, построить линии тренда (линии регрессии), используя следующие аппроксимирующие функции:
- линейную,
- экспоненциальную,
- логарифмическую,
- степенную.
3) найти оценки коэффициентов уравнения регрессии и определить достоверность аппроксимации для каждой функции, заполнить таблицу 4.
Таблица 4 – Уравнения регрессии и достоверность аппроксимации
| Аппроксимирующая функция | Уравнение линии тренда | Достоверность аппроксимации |
| Линейная | ||
| Экспоненциальная | ||
| Логарифмическая | ||
| Степенная |
4) определить тесноту связи между среднедушевым доходом и расходами на потребление, вычислить коэффициент корреляции;
5) определить эластичность потребления по доходу и сделать выводы.
Источник https://www.studfiles.ru/preview/2864817/page:15/
Краткие сведения
Тренд – это функция заданного вида, с помощью которой можно аппроксимировать построенный по данным таблицы график. Тренд служит для выявления тенденций развития процесса, представленного в виде диаграммы, и обеспечивает прогноз на заданный период.
В MS Excel предусмотрено несколько стандартных типов тренда: линейный, логарифмический, степенной, экспоненциальный, полиномиальный, скользящее среднее. Необходимые условия для построения тренда: период времени, за который изучается исследуемый процесс, должен быть достаточным для выявления закономерности; тренд в анализируемый период должен развиваться эволюционно; процесс, представленный диаграммой, должен обладать определенной инертностью.
Тренд можно строить для диаграмм типа: линейчатый график, гистограмма, диаграмма с областями, XY-точеная диаграмма.
При установлении наиболее подходящего типа регрессионной зависимости для описания процесса изменения показателей какой-либо величины используют показатель достоверности описания функции. Тип регрессионной линии считается установленным, если величина достоверности аппроксимации R2 =1. Однако, если аппроксимации R2 менее 0,6 уместно говорить о том, что тип зависимости для описания процесса изменения показателя не подходит. Если ни в одном из вариантов исследуемых типов регрессионных линий (трендов) величина достоверности аппроксимации не равна единице, то выбирают тот тип, для которого величина достоверности аппроксимации максимальна.
Корреляция - это зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.
Различают следующие виды корреляции:
· парная корреляция - связь между двумя признаками (результативным и факторным, или двумя факторными);
· частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;
· множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.
Задачей корреляционного анализа является количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при многофакторной связи).
Теснота связи количественно выражается величиной коэффициентов корреляции, которые давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» факторных признаков при построении уравнения множественной регрессии.
Теснота связи показывает меру влияния факторного признака на общую вариацию результативного признака. Классификация связи по степени тесноты представлена в таблице 5.
Таблица 5 - Количественные критерии оценки тесноты связи
| Величина коэффициента корреляции | Характер связи |
| До ±0,3 | Практически отсутствует |
| От ±0,3 до ±0,5 | Слабая |
| От ±0,5 до ±0,7 | Умеренная |
| От ±0,7 до ±1,0 | Сильная |
Корреляция взаимосвязана с регрессией, поскольку первая оценивает силу (тесноту) связи, вторая исследует ее форму.
Регрессионный анализ заключается в определении аналитического выражения связи в виде уравнения регрессии.
Регрессией называется зависимость среднего значения случайной величины результативного признака от величины факторного, а уравнением регрессии – уравнение, описывающее корреляционную зависимость между результативным признаком и одним или несколькими факторными.
Задача 4.
Имеются данные о значениях показателей: X1 – среднедушевой доход, ден. ед.; X2 – цена товара, ден. ед.; Y – расходы на потребление, ден. ед. (таблица 6).
Таблица 6 - Варианты исходных данных для выполнения задания 2
| Вариант 2.1 | Вариант 2.2 | Вариант 2.3 | Вариант 2.4 | Вариант 2.5 | ||||||||||
| Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У |
| Вариант 2.6 | Вариант 2.7 | Вариант 2.8 | Вариант 2.9 | Вариант 2.10 | ||||||||||
| Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У | Х1 | Х2 | У |
Предполагая, что между переменными Y, X 1, X 2 существует линейная зависимость.
Требуется:
1) построить функцию спроса;
2) определить частные коэффициенты корреляции, построив матрицу парных коэффициентов корреляции, и сделать выводы о направлении и силе связи между переменными, а также о возможных связях между факторами спроса (присутствии мультиколлинеарности в модели регрессии);
4) определить достоверность аппроксимации, вычислив коэффициент детерминации;
5) дать экономическую интерпретацию коэффициентов регрессии, найти эластичность потребления по доходу и цене товара, сделать экономические выводы.
Примечание: Вычисления произвести с помощью пакета (надстройки) «Анализ данных» MS EXCEL. Доверительная вероятность γ = 0,95 (значимость α = 0,05).