Задание: Конструкция состоит из двух частей. Установить, при каком способе соединения частей конструкции модуль реакции 
наименьший, и для этого варианта соединения определить реакции опор, а также соединения С.
Дано: 
= 9,0 кН; 
= 12,0 кН;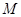 
= 26,0 кН 
м; 
= 4,0 кН/м.
Схема конструкции представлена на рис.1.
Рис.1. Схема исследуемой конструкции.
Решение:
1) Определение реакции опоры А при шарнирном соединении в точке С.
Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.2.). Составим уравнение моментов сил относительно точки B.
Рис.2.
(1)
где 
кН.
После подстановки данных и вычислений уравнение (1) получает вид:
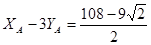кН (1’)
Второе уравнение с неизвестными 
и 
получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 3):
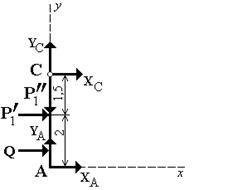
Рис. 3.
.
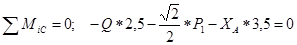Отсюда находим, что
кН.
Подставив найденное значение в уравнение (1’) найдем значение 
:
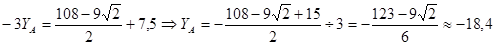кН.
Модуль реакции опоры А при шарнирном соединении в точке С равен:
кН.
2) Расчетная схема при соединении частей конструкции в точке С скользящей заделкой, показанной на рис. 4.
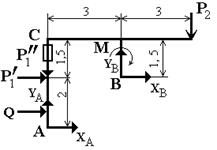
Рис. 4
Системы сил, показанные на рис. 2 и 4, ничем друг от друга не отличаются. Поэтому уравнение (1’) остается в силе. Для получения второго уравнения рассмотрим систему уравновешивающихся сил, приложенных к части конструкции, располоденной левее скользящей заделки С (рис. 5).
Рис. 5
Составим уравнение равновесия:
и из уравнения (1’) находим:
Следовательно, модуль реакции при скользящей заделке в шарнире С равен:
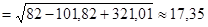кН.
Итак, при соединении в точке С скользящей заделкой модуль реакции опоры А меньше, чем при шарнирном соединении (≈ 13%). Найдем составляющие реакции опоры В и скользящей заделки.
Для левой от С части (рис. 5а)
,
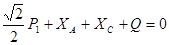кН.
Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений равновесия, составленных для правой от С части конструкции.
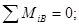
кН*м
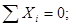
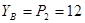кН
; 
кН
Результаты расчета приведены в таблице 1.
Таблица 1.
| Силы, кН | Момент, кН*м | ||||||
| XA | YA | RA | XC | XB | YB | MC | |
| Для схемы на рис. 2 | -7,5 | -18,4 | 19,9 | - | - | - | - |
| Для схемы на рис. 4 | -14,36 | -11,09 | 17,35 | -28,8 | 28,8 | 12,0 | -17,2 |
Дано:
R2=15; r2=10; R3=20; r3=20
X=C2t2+C1t+C0
При t=0 x0=8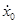 
=4
t2=2 x2=44 см
X0=2C2t+C1
C0=8
C1=4
44=C2 *22+4*2+8
4C2=44-8-8=28
C2=7
X=7t2+4t+8
=V=14t+4
a=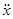 
=14
V=r2 
2
R2 2=R3 3
3=V*R2/(r2*R3)=(14t+4)*15/10*20=1,05t+0,3
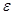3= 3=1,05
Vm=r3* 3=20*(1,05t+0,3)=21t+6
atm=r3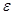
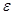=1,05t
atm=R3 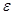=20*1,05t=21t
anm=R3 23=20*(1,05t+0,3)2=20*(1,05(t+0,28)2
a= 
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Исходные данные.
Механическая система под действием сил тяжести приходит в движение из состояния покоя. Трение скольжения тела 1 и сопротивление качению тела 3 отсутствует. Массой водила пренебречь.
Массы тел - m1, m2, m3, m4; R2, R3, R4 – радиусы окружностей.
| m1, кг | m2, кг | m3, кг | m4, кг | R2, см | R3, см | s, м |
| m | m/10 | m/20 | m/10 | 0.05π |
Найти.
Пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определит скорость тела 1 в тот момент, когда пройденный им путь станет равным s.
Решение.
1. Применим к механической системетеорему об изменении кинетической энергии.
,
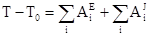где T0 и T – кинетическая энергия системы в начальном и конечном положениях; 
– сумма работ внешних сил, приложенных к системе, на перемещении из начального положения в конечное;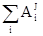 
- сумма работ внутренних сил системы на том же перемещении.
Для рассматриваемых систем, состоящих из абсолютно твёрдых тел, соединённых нерастяжимыми нитями и стержнями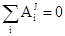 
. Так как в начальном положении система находится в покое, то T0=0.
Следовательно, уравнение (1) принимает вид:
.
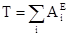2. Определим угол, на который повернётся водило, когда груз 1 пройдёт расстояние s.
.
То есть когда груз 1 пройдёт путь s, система повернётся на угол 90º.
3. Вычислим кинетическую энергию системы в конечном положении как сумму кинетических энергий тел 1, 2, 3, 4.
T = T1 + T2 + T3 + T4.
а) Кинетическая энергия груза 1, движущегося поступательно равна:
.
б) Кинетическая энергия катка 2, вращающегося вокруг своей оси равна:
,
где 
- момент инерции катка 2, 
- угловая скорость катка 2.
Отсюда получаем, что
.
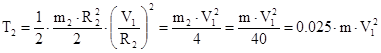в) Кинетическая энергия катка 3, совершающего плоско-параллельное движение, равна:
,
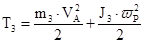где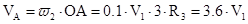 
- скорость центра масс катка 3,
-угловая скорость мгновенного центра скоростей катка 3
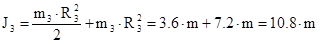
момент инерции катка 3 относительно мгновенного центра скоростей.
Отсюда получаем, что
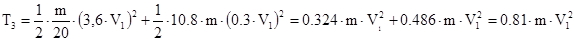
г) Кинетическая энергия катка 4, совершающего плоскопараллельное движение, равна:
где 
- угловая скорость мгновенного центра скоростей,
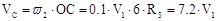- скорость центра масс катка 4,
- момент инерции катка 4 относительно мгновенного центра скоростей.
Отсюда получаем, что
Таким образом, кинетическая энергия всей механической системы равна:
4. Найдём работу всех внешних сил, приложенных к системе на заданном перемещении.
а) Работа силы тяжести G1: AG1=m1∙g∙s=m∙980∙5=15386∙m1.
б) Работа силы тяжести G2: AG2=0.
в) Работа силы тяжести G3: AG3=-m3∙g∙(OA)=-0.05∙m∙980∙36=-1764∙m.
г) Работа силы тяжести G4: AG4=-m4∙g∙OC=-0.1∙m∙980∙72=-7056∙m.
Таким образом, работа всех внешних сил, приложенных к системе равна:
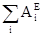= AG1+AG3+AG4=15386∙m-1764∙m-7056∙m=6566∙m.
5. Согласно теореме об изменении кинетической энергии механической системы приравниваем значения T и .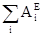
=6566∙m;
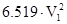=6566.
Отсюда скорость тела 1 равна:
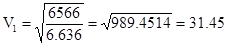= 0.31 м/с.
Результаты расчётов.
| V1, м/c |
| 0.31 |
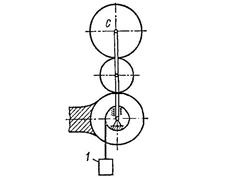
Дано: Q=4kH, G=2kH, a=50см, b=30см.
Определить: реакции опор А, В, С.
Решение:
1) ∑FKX=XA+XB-RC∙cos30°+Q·sin45°=0;
2) ∑FKY=YA=0;
3) ∑FKZ=ZA+ZB+RC·sin30°-G-Q·cos45°=0;
4) ∑MKX=ZB·AB-G·AB/2-Q·cos45°·AB=0;
5) ∑MKY=G·AC/2·cos30°-RC·AC·sin60°+Q·AC·sin75°=0;
6) ∑MKZ=-XB·АВ-Q·AB·cos45°=0.
Из (6) XB=(-Q·AB·cos45°)/АВ=-4·50·0,7/50=-2,8кН
Из (5) RC=(G·AC/2·cos30°+Q·AC·sin75°)/AC·sin60°=
=(2·30/2·0,87+4·30·0,96)/30·0,87=(26,1+115,2)/26,1=5,4кН
Из (4) ZB=(G·AB/2+Q·cos45°·AB)/AB=(50+141,4)/50=3,8kH
Из (3) ZA=-ZB-RC·sin30°+G+Q·cos45°=-3,8-2,7+2+2,8=-1,7кН
Из (1) XA=-XB+RC∙cos30°-Q·sin45°=2,8+4,7-2,8=4,7кН
Результаты вычислений:
| Силы, кН | |||||
| RC | XA | YA | ZA | XB | ZB |
| 5,4 | 4,7 | -1,7 | -2,8 | 3,8 |