Определение реакций опор составной конструкции (система двух тел)
Задание: Конструкция состоит из двух частей. Установить, при каком способе соединения частей конструкции модуль реакции 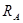 наименьший, и для этого варианта соединения определить реакции опор, а также соединения С.
наименьший, и для этого варианта соединения определить реакции опор, а также соединения С.
Дано:  = 9,0 кН;
= 9,0 кН; 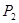 = 12,0 кН;
= 12,0 кН; 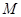 = 26,0 кН
= 26,0 кН 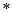 м;
м;  = 4,0 кН/м.
= 4,0 кН/м.
Схема конструкции представлена на рис.1.
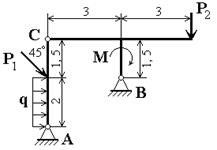
Рис.1. Схема исследуемой конструкции.
Решение:
1) Определение реакции опоры А при шарнирном соединении в точке С.
Рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.2.). Составим уравнение моментов сил относительно точки B.
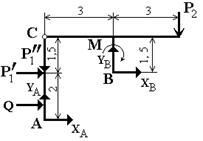
Рис.2.
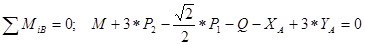 (1)
(1)
где 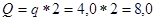 кН.
кН.
После подстановки данных и вычислений уравнение (1) получает вид:
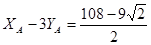 кН (1’)
кН (1’)
Второе уравнение с неизвестными  и
и 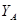 получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 3):
получим, рассмотрев систему уравновешивающихся сил, приложенных к части конструкции, расположенной левее шарнира С (рис. 3):

Рис. 3.
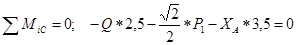 .
.
Отсюда находим, что
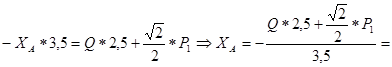
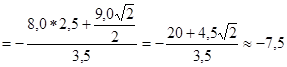 кН.
кН.
Подставив найденное значение  в уравнение (1’) найдем значение
в уравнение (1’) найдем значение 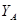 :
:
 кН.
кН.
Модуль реакции опоры А при шарнирном соединении в точке С равен:
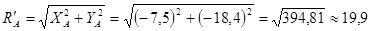 кН.
кН.
2) Расчетная схема при соединении частей конструкции в точке С скользящей заделкой, показанной на рис. 4.
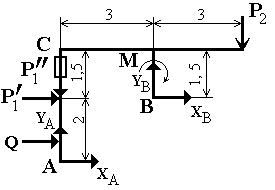
Рис. 4
Системы сил, показанные на рис. 2 и 4, ничем друг от друга не отличаются. Поэтому уравнение (1’) остается в силе. Для получения второго уравнения рассмотрим систему уравновешивающихся сил, приложенных к части конструкции, располоденной левее скользящей заделки С (рис. 5).
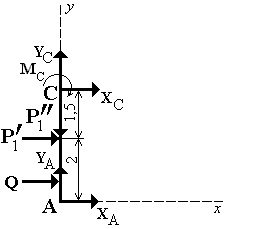
Рис. 5
Составим уравнение равновесия:
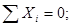

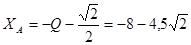
и из уравнения (1’) находим:
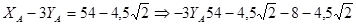

Следовательно, модуль реакции при скользящей заделке в шарнире С равен:
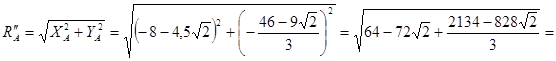
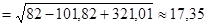 кН.
кН.
Итак, при соединении в точке С скользящей заделкой модуль реакции опоры А меньше, чем при шарнирном соединении (≈ 13%). Найдем составляющие реакции опоры В и скользящей заделки.
Для левой от С части (рис. 5а)

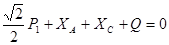 ,
,
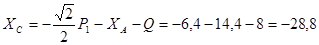 кН.
кН.
Составляющие реакции опоры В и момент в скользящей заделке найдем из уравнений равновесия, составленных для правой от С части конструкции.
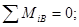
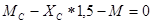
 кН*м
кН*м

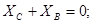
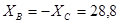 кН
кН

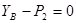 ;
;  кН
кН
Результаты расчета приведены в таблице 1.
Таблица 1.
| Силы, кН | Момент, кН*м | ||||||
| XA | YA | RA | XC | XB | YB | MC | |
| Для схемы на рис. 2 | -7,5 | -18,4 | 19,9 | - | - | - | - |
| Для схемы на рис. 4 | -14,36 | -11,09 | 17,35 | -28,8 | 28,8 | 12,0 | -17,2 |
Определение реакций опор твердого тела
Задание: Найти реакции опор конструкции. Схема конструкции показана на рисунке 1. Необходимые данные для расчета приведены в таблице 1.
Табл. 1
| Силы, кН | Размеры, см | |||||
 
| 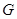
| a | b | c | R | r |

Рис. 1. Здесь:  ,
, 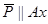 ,
,  ,
, 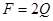 .
.
Решение: К конструкции приложены сила тяжести 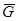 , силы
, силы  и реакции опор шарниров
и реакции опор шарниров 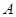 и
и  :
: 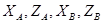 (рис. 2)
(рис. 2)

Рис. 2.
Из этих сил пять неизвестных. Для их определения можно составить пять уравнений равновесия.
Уравнения моментов сил относительно координатных осей:
 ;
;
 ;
;
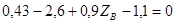 ;
; 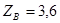 кН.
кН.
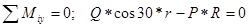 ;
;
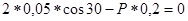 ;
;  кН.
кН.
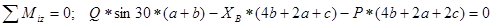 ;
;
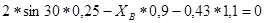 ;
; 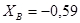 кН.
кН.
Уравнения проекций сли на оси координат:
 ;
;
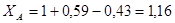 кН
кН
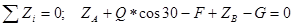 ;
;
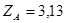 кН.
кН.
Результаты измерений сведены в табл. 2.

| 
| 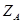
| 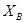
| 
|
| 0,43 кН | 1,16 кН | 3,13 кН | -0,59 кН | 3,6 кН |
Интегрирование дифференциальных уравнений
Дано
a=45°; Vв=2Va; τ=1c; L=3 м; h=6
Найти ƒ=? d=?
Решение
mX=SXi 1 Fтр=fN
mX=Gsina-Fcoпр N=Gcosa
mX=Gsina-fGcosa
a
X=gsina-fgcosa
X=(g(sina-fcosa) t+ C1
X=(g(sina-fcosa)/2) t2+ C1t+ C2
При нормальных условиях: t=0 x=0
X=C1 X= C2=> C1=0
X=g(sina-fcosa) t+ 1 X=(g(sina-fcosa)/2) t2
X=Vв X=L
Vв=g(sinα-ƒ*cosα)τ
L=((g(sinα-ƒ*cosα)τ)/2)τ
ƒ=tgα-(2L/τ *g*cosα)=1-0,8=0,2
Vв=2l/τ=6/1=6м/с
Рассмотрим движение тела от точки В до точки С показав силу тяжести действующую на тело, составим дифференциальное уравнение его движения. mx=0 my=0
Начальные условия задачи: при t=0
X0=0 Y0=0
X0=Vв*cosα; Y0=Vв*sinα
Интегрируем уравнения дважды
Х=C3 Y=gt+C4
X= C3t+ C5
Y=gt /2+C4t+C6, при t=0
X=C3; Y0=C4
X=C5; Y0=C6
Получим уравнения проекций скоростей тела.
X=Vв*cosα, Y=gt+Vв*sinα
и уравнения его движения
X=Vв*cosα*t Y=gt /2+Vв*sinα*t
Уравнение траектории тела найдем, исключив параметр t из уравнения движения. Получим уравнение параболы.
Y=gx /2(2Vв*cosα) + xtgα
В момент падения y=h x=d
d=h/tgβ=6/1=6м
Ответ: ƒ=0,2 d=6 м