"удовлетворенности учебой
"
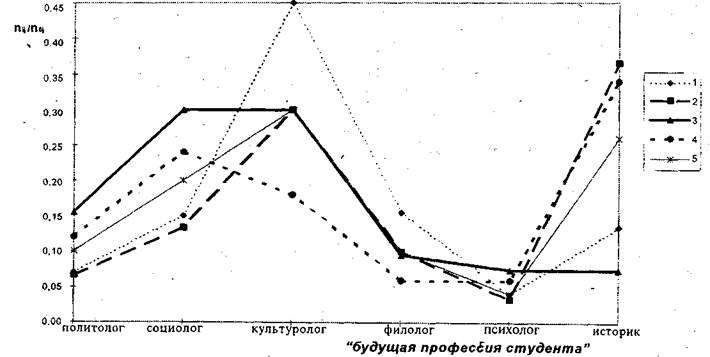
Рис. 3.3.2.
группами. Для построения этих кривых используем четвертый показатель таблицы сопряженности. В таблице 3.3.2 значения этого показателя находятся под чертой. Для того чтобы построить, к примеру, эмпирическую кривую распределения студентов по их будущим профессиям для третьей группы по степени Удовлетворенности (частично удовлетворенные и частично неудовлетворенные), из таблицы 3.3.2 выделим столбец со значениями (0,16, 0,30, 0,30, 0,10, 0,08, 0,08). Это доли шести профессиональных групп в совокупности удовлетворенных учебой на тройку. Аналогичным образом строятся и другие четыре кривые распределения.
Из визуального сравнения пяти построенных эмпирических кривых распределения видим следующее:
· похожесть профессиональных структур наблюдается только для третьей и четвертой групп по удовлетворенности учебой.
· практически в, каждой группе, кроме этих двух, по удовлетворенности своя собственная профессиональная структура.
· из этого делаем следующий вывод: что признаки «будущая профессия» и «удовлетворенности учебой» статистически (по данным) связаны.
Формально можно говорить о влиянии удовлетворенности на профессию, но содержательно это не имеет никакого смысла.
Важно заранее определить, какой из признаков может содержательно зависеть от другого. Отсюда возникают понятия зависимый (целевой) и независимый признак. Дихотомия «направленная ¾ ненаправленная» связь является важной в понимании свя3и.
Деление на зависимые ¾ независимые признаки в социологии не всегда содержательно обосновано. Зачастую такое деление необходимо в процессе анализа и носит функциональный характер. В том смысле, что один и тот же признак независимо От его содержания в одной задаче может выступать в роли зависимого, а в другой ¾ в роли независимого.
Можно заметить следующее. Представим себе, что все кривые на каждом из рисунков похожи между собой. Что это означает для социолога? Во-первых, это значит, что профессиональная структура в группах студентов с различной степенью удовлетворенности учебой одинакова и не зависит от этой степени. При этом она (структура) такая же, как и профессиональная структура для всей совокупности студентов-гуманитариев (маргинальные частоты по строкам). Во-вторых, это значит, что структура удовлетворенности во всех профессиональных группах одинакова и не зависит от будущей профессии студента. При этом эта структура такая же, как во всей совокупности (маргинальные частоты по столбцам). Тогда связь между феноменами «профессия» и «удовлетворенность» отсутствует, статистическая связь не наблюдается. Наши признаки статистически независимы.
В исследованиях такая ситуация практически не встречается, и не потому, что отсутствие связи не наблюдается, а совсем по другим причинам. Основная причина ¾ специфика наших социологических данных. Это их неустойчивый характер. Например, это проявляется в неточности измерения того же феномена, как удовлетворенность учебой. Причин тому множество. Это и несовершенство методик измерения, и неустойчивость ответов респондента, и плохая выборка. Ясно одно, всегда имеет место влияние многих случайных и неслучайных факторов на конкретные значения изучаемого нами признака. С неслучайными факторами социолог может бороться, а случайные будут иметь место всегда. Поэтому социолог делает выводы с учетом этой ситуации. Задается уровнем «ошибиться». Статистическая независимость констатируется не в идеальном случае, а в случае, близком к идеальному.
Представим себе противоположную ситуацию, когда на каждом из рисунков все кривые непохожи, несхожи. Для социолога это означает, что в каждой группе с разной степенью удовлетворенности учебой своя собственная профессиональная структура. В каждой профессиональной группе своя собственная структура удовлетворенности. Из этого следует, что будущая профессия студента связана с его удовлетворенностью учебой, наблюдается сильная статистическая зависимость. Естественно, такая ситуация в исследованиях тоже практически не встречается.
Реальные рисунки трудно поддаются визуальной интерпретации. К тому же в исследовании их бывает очень много. Отсюда и возникает необходимость в количественных оценках степени взаимосвязи между признаками, в определении, сильное или слабое влияние признаков друг на друга. Это можно сделать с помощью различных мер взаимосвязи. Мы подошли к важным понятиям меры связи, или коэффициенты связи. Таких мер много, так как много различных интерпретаций понятия «связь». Другими словами, связь может пониматься по-разному. Это во-первых. Во-вторых, даже в рамках одного и того же понимания связи существуют различные способы ее математической формализации..
Прежде чем рассмотреть различные коэффициенты связи, введем дихотомические пары понятий, без которых невозможно перейти к эмпирической интерпретации понятия «связь». Некоторые из этих пар были упомянуты выше: зависимый признак ¾ независимый, направленная связь ¾ ненаправленная, статистическая зависимость ¾ независимость, сильная (тесная) связь ¾ слабая.
Пара понятий: функциональная связь ¾ корреляционная связь. Функциональной связью между двумя признаками называется такая связь, когда одному и тому же значению одного признака соответствует одно или несколько значений другого. Геометрически ¾ это красивые плавные кривые (прямая, парабола, синусоида и т. д.) или кривые с точкой разрыва (гипербола). Функциональные связи в социологии встречаются в основном при работе с данными первого типа. Примером функции является и любой аналитический индекс.
При рассмотрении связи между двумя признаками в рамках других типов информации наблюдается другая картина ¾ одному и тому же значению признака соответствует целое распределение значений по-другому из признаков. Такая связь называется корреляционной. Эти связи между двумя признаками геометрически могут быть изображены в виде облаков точек в двумерном пространстве, т. е. на плоскости.
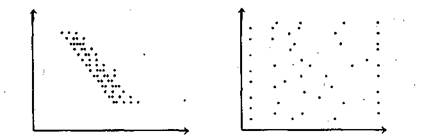
Рис. 3.3.3 Сильная связь Рис. 3.3.4 Слабая связь
Корреляционная связь может быть сильной и слабой. В первом случае облако точек имеет четкую конфигурацию, четкую закономерность. Если признаки имеют метрический уровень измерения, то можно сказать, что с ростом значений одного признака растет в среднем и значение другого. Здесь наблюдаем линейную связь. Эта закономерность может быть описана посредством прямой линии, которая называется линией регрессии. Разумеется, корреляционная связь может быть и нелинейной, т. е. описываться не прямыми.
Важно, что корреляционные связи могут быть описаны с помощью функциональных. Другими словами, социологу правомерно ставить вопрос, насколько корреляционная связь отличается от заданной им (в виде гипотезы) функциональной. Практически все коэффициенты качественной вариации основаны на оценке степени отклонения от равномерного распределения (от прямой линии).
Социолог сталкивается с необходимостью задавать или выбирать функциональные зависимости при работе с любым из пяти типов информации. При работе с динамическими рядами главная задача ¾ построить, подобрать функцию, описывающую этот ряд. Многие математические методы предполагают задание характера зависимости изучаемых признаков. Правда, из этого не следует, что мы всегда найдем функцию, подходящую для описания эмпирической закономерности.
Существует мера связи в предположении, что корреляционная связь носит линейный характер и признаки имеют метрический уровень измерения. Такая мера называется коэффициентом линейной связи Пирсона.
Целесообразно также использование такой пары понятий, как глобальные ¾ локальные меры связи. Эта пара понятий необходима для условного обозначения следующей ситуации.
Вернемся к таблице сопряженности для нашего случая. Связь между будущей профессией студента и удовлетворенностью учебой можно описать, сравнивая их условные распределения. Меры, отражающие эту целостность, можно определить условно как меры «глобального» характера для таблицы сопряженности. К такого рода мерам относятся коэффициенты, основанные на величине «хи-квадрат» и Гудмена-Краскала.
В то же время можно поставить вопрос о связи следующим образом. Например, связана ли самая низкая удовлетворенность учебой со второй профессией (социолог). Тогда речь идет условно как бы о связях в локальном смысле. Для таких случаев существуют также коэффициенты связи. Это такие коэффициенты, как коэффициент Юла, показатели детерминации.
Вместо рассмотренной пары направленная связь ¾ ненаправленная можно пользоваться терминами: симметричная связь ¾ асимметричная. При вычислении направленных коэффициентов связи между признаками X и Y, как правило, оказывается, что значение коэффициента для X® Y не равно значению для ХY. Два признака неравноправны, их нельзя формально поменять местами. Отсюда возникают асимметричные коэффициенты. Они не всегда удобны для использования в сложных математических методах. Потому при двух асимметричных коэффициентах всегда существует третий, как бы их усредняющий. Мы столкнемся с тройкой мер Гуттмана и с тройкой мер Гудмена - Краскала.
Перейдем к рассмотрению взаимосвязанных пар понятий, таких, как непосредственная связь ¾ опосредованная связь; истинное (значение коэффициента) ¾ложное. Первая пара понятий важна при интерпретации количественного значения коэффициента связи. По таким значениям не всегда ложно говорить о силе связи (сильная ¾ слабая). В ряде случаев просто констатируется наличие или отсутствие определенным образом понимаемой связи. Если по конкретному значению коэффициента мы видим, что связь есть, то это вовсе не означает существования в реальности непосредственной связи между двумя изучаемыми признаками, а может означать наличие опосредованной связи. Отсюда вторая пара понятий: истинное значение ¾ ложное.
В литературе тому есть множество примеров. Например, в США за 1870—1910 годы было установлено наличие связи между заработной платой учителей и потреблением вина. Это пример ложной связи. Ибо она была опосредована тем, что в эти годы наблюдался промышленный бум и рост заработной платы и тем самым рост потребления вина во всех группах населения.
В нашем случае можно сказать, что связь между будущей профессией студента и удовлетворенностью учебой есть. Но она может носить ложный характер, т.е. опосредована другими признаками. Например, социальным происхождением, успеваемостью, удовлетворенностью жизнью, уверенностью в завтрашнем дне и т. д.
Возможна и другая ситуация, когда значение коэффициента связи указывает на ее отсутствие, а на самом деле связь существует. Пример приведем в следующем разделе книги для случая таких признаков, как удовлетворенность собой и удовлетворенность жизнью.
Еще несколько слов о статистической зависимости ¾ статистической независимости. Это очень важные понятия. Вернемся опять к нашей таблице сопряженности и задаче сравнения условных распределений. Выше, исходя из элементарного здравого смысла, мы пришли к необходимости использования направленных мер связи для определения различия в структурах распределения. Тем самым для определения: наблюдается ли статистическая зависимость между будущей профессией студента и удовлетворенностью учебой. Но для определения статистической зависимости можно исходить и из другой модели, из других соображений. Поставим вопрос так. Какая величина может стоять в ячейке таблицы сопряженности, если эти признаки статистически независимы? Разумеется, такой вопрос правомерен. При этом маргинальные частоты (одномерные, простые) нам известны по нашей выборке.
Рассмотрим, к примеру, ячейку (2,1). Она соответствует будущим социологам, неудовлетворенным учебой. Статистическую независимость признаков «будущая профессия» и «удовлетворенность учебой» можем понимать следующим образом. Доля неудовлетворенных учебой социологов среди всех студентов-социологов равна доле не удовлетворенных учебой студентов среди всех студентов-гуманитариев. Ведь такое понимание связи не должно вызывать у вас неприятия, ибо не противоречит здравому смыслу социолога. Тогда в ситуации статистической независимости легко определяется то значение, которое должно стоять в нашей ячейке. Оно вычисляется исходя из упомянутой выше пропорции. К ней мы вернемся при рассмотрении мер связи, основанных на так называемой величине «хи-квадрат».
Многие коэффициенты связи как раз и определяют отклонение реальных частот (того, что получено по выборке) от частот как бы теоретических, т. е. вычисленных по той же таблице, но для случая статистической независимости.
И наконец, обратим внимание еще на одну пару понятий. Социолога интересует связь между признаками для выявления причинно-следственных отношений между признаками. Поэтому он изучает связи всегда в контексте: влияет ¾ не влияет; детерминирует ¾ не детерминирует; увеличивает информацию ¾ не увеличивает; улучшает прогноз ¾ не улучшает и т. д. После всех наших предыдущих рассуждений является очевидным, что наличие корреляционной связи не говорит о причинности [3. с. 72—119; 11. с. 43—63]. И в то же время для причинного анализа невозможно обойтись без изучения корреляционных связей. Термином «причинный анализ» принято обозначать специфический класс математических методов. Вместе с тем проблема причинности в нашей науке очень интересная, сложная область, которую нельзя свести только к классу математических методов.
Итак, мы познакомились с дихотомическими парами понятий, которые важны для изучения и понимания связи:
причинная ¾ корреляционная;
функциональная ¾ корреляционная;
направленная ¾ ненаправленная;
локальная ¾ глобальная;
истинная ¾ложная;
статистическая зависимость ¾ статистическая независимость; симметричная ¾ асимметричная;
непосредственная ¾ опосредованная;
линейная ¾ нелинейная.
Коэффициенты связи, меры связи бывают не только но и частные, множественные. Различают коэффициенты для номинального, порядкового, метрического уровня измерения. Сами таблицы сопряженности бывают разные. Они бывают и многомерные, если сопрягаются несколько признаков, и тогда их называют таблицами с несколькими входами.
Очень интересной в социологии является таблица сопряженности квадратного вида (число строк равно числу столбцов), когда сопрягается признак с самим собой. Она возникает в ситуации панельного исследования. Представим себе, что тех же студентов-гуманитариев мы опросили повторно через пару лет. Тогда таблица для двух признаков, например, «уверенность в завтрашнем дне в 1997 году» и «уверенность в завтрашнем дне в 1999 году», позволит изучить степень изменчивости такой уверенности. Для анализа таких таблиц сопряженности существуют специфические меры связи.