Задача №3 «Транспортная задача»

Задача №3 «Транспортная задача»

Задача №4 «Назначение на работы»

Задача №2 «Планирование портфеля заказов»

Задача №1 «Планирование производства»

Небольшая фабрика выпускает два типа красок: для внутренних (I) и наружных (Е) работ.

Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 10 и 16 тонн, соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в табл. 2.1.

Таблица 2.1

Исходные данные задачи о планировании производства красок

Исходный продукт	Расход исходных продуктов на 1 т краски, т	Максимально возможный запас, т
краска Е	краска І
А В

Минимальный суточный спрос на краску для внутренних работ составляет 1 т, а для внешних работ 2 т. Суточный спрос на краску i никогда не превышает спроса на краску Е более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3000 руб. для краски Е и 2000 руб. для краски I.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

В нашем случае фабрике необходимо спланировать объем производства красок так, чтобы максимизировать прибыль. Поэтому переменными являются:

Хi — суточный объем производства краски I и Хе — суточный объем производства краски Е.

Суммарная суточная прибыль от производства Xi краски I и Xe краски Е равна

Z = 3000*Хe+ 2000*Xi (2.1)

Целью фабрики является определение среди всех допустимых значений Xi и Xe таких, которые максимизируют суммарную прибыль, т. е, целевую функцию Z.

Перейдем к ограничениям, которые налагаются на Xe и Xi. Объем производства красок не может быть отрицательным, следовательно:

Хt, Хi > 0 (2.2)

Расход исходного продукта для производства обоих видов красок не может превосходить максимально возможный запас данного исходного продукта, следовательно:

Хe + 2Xi <= 10 (2.3)

2Xe + Xi <= 16 (2.4)

Кроме того, ограничения на величину спроса на краски таковы:

Xi-Xe <= 1 (2.5)

Xi < 2 (2.6)

Таким образом, математическая модель данной задачи имеет следующий вид:

максимизировать

Z= 300Хe + 2000Xi

при следующих ограничениях:

Xe+2Xi<= 10

2Xe+Xi<= 16

Xi-Xe<=1

Xi<=2

Xi, Xe>=0

Заметим, что данная модель является линейной, т. к. целевая функция 1-ограничения линейно зависят от переменных.

Вводим данные в таблицу Excel.

Покажем формулы

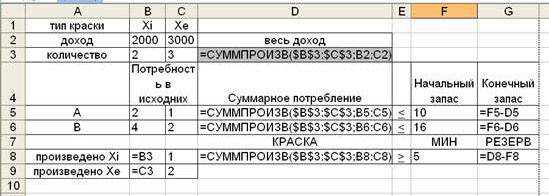
Решим данную задачу с помощью команды Сервис - Поиск решения Excel. Средство поиска решений является одной из надстроек Excel. Если в меню Сервис отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис, Надстройки, Поиск решения.

Для того чтобы получить максимальный доход надо произвести краски І 1 т., а краски Е 6 т.

Задача №3 «Транспортная задача»

Предположим, что фирма имеет 4 фабрики и 5 центров распределения ее товаров. Фабрики фирмы располагаются в А, Б, В, Г с производственными возможностями 200, 150, 225 и 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в 1, 2, 3, 4, 5 с потребностями в 100, 200, 50, 250 и 150 единиц продукции ежедневно, соответственно. Хранение на фабрике единицы продукции, не поставленной в центр распределения, обходится в $0,75 в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен $2,5 в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в табл. 2.6.

Таблица 2.6 - Транспортные расходы

	1	2	3	4	5
А	1	2	7	12	1
Б	2	7	9	12	2
В	3	4	6	4	3
Г	7	3	11	3	5

Необходимо так спланировать перевозки, чтобы минимизировать суммарные транспортные расходы.

Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции. В противном случае в модель нужно было бы ввести:

В случае перепроизводства — фиктивный пункт распределения, стоимость перевозок единицы продукции в который полагается равной стоимости складирования, а объемы перевозок — объемам складирования излишков продукции на фабриках

В случае дефицита — фиктивную фабрику, стоимость перевозок единицы продукции с которой полагается равной стоимости штрафов за недопоставку продукции, а объемы перевозок — объемам недопоставок продукции в пункты распределения.

Для решения данной задачи построим ее математическую модель. Неизвестными в данной задаче являются объемы перевозок. Пусть Хij — объем перевозок с i-й фабрики в j-й центр распределения.

Функция цели — это суммарные транспортные расходы, т. е.

Z=SScij*xij (2.22)

Сij— стоимость перевозки единицы продукции с i-й фабрики j-й центр распределения.

Неизвестные в данной задаче должны удовлетворять следующим ограничениям:

объемы перевозок не могут быть отрицательными;

так как модель сбалансирована, то вся продукция должна быть вывезена с фабрик, а потребности всех центров распределения должны быть полностью удовлетворены.

В результате имеем следующую модель:

минимизировать:

Z=SScij*xij (2.23)

при ограничениях:

Sxij= вj,,j=[1, 5] (2.24)

Sxij=ai, i=[1,4], (2.25)

xij>=0, i=[1,4], j= [1,5]. (2.26)

где аi — объем производства на i-й фабрике, вi — спрос вj-м центре распределения.

Ввод данных