Тема 2. Лекция 5. Механические передачи. Цилиндрические передачи
с эвольвентным профилем.
Цилиндрическая зубчатая передача представляет собой механизм, предназначенный для передачи непрерывного вращательного движения, в котором подвижными звеньями являются зубчатые колеса со взаимно параллельными осями, а контактирующие поверхности цилиндрические. Непрерывность передачи вращательного движения обеспечивается замкнутой системой зубьев колес, векторы линейных относительных скоростей которых направлены вдоль их общей касательной к линиям зубьев, лежащим на взаимокасающихся поверхностях, называемых начальными поверхностями. Концентрические окружности колес передачи, принадлежащие начальным поверхностям, называют начальными окружностями.
На основании теоремы о соотношении скоростей в высшей кинематической паре (контакт точечный или линейный), устанавливающей мгновенный центр вращения, общая нормаль в точке контакта сопряженных профилей зубьев колес, называемая полюсом зацепления W, делит расстояние между центрами вращения колес 1 и 2 на отрезки, обратно пропорциональные угловым скоростям w1 и w2. Эти отрезки являются радиусами начальных окружностей r w1 и r w2 колес 1 и 2, а их соотношение устанавливает параметры передаточной функции механизма, выраженные передаточным отношением i
i =w1 / w2=r w2 / r w1. (2.74)
Относительные линейные скорости на начальных окружностях равны
vw 1 = w1× rw1; (2.75)
vw2 = w2× rw2. (2.76)
В случае, когда величины линейных скоростей на начальных окружностях колес равны между собой, и угловые скорости w1 и w2 имеют неизменный характер, передаточная функция является величиной постоянной, что отражает основной закон зацепления, а вращательное движение будет равномерным.
|
|
При постоянном передаточном отношении расстояния между соседними профилями зубьев по начальным окружностям одинаковы, поэтому отношение числа зубьев z2 к числу зубьев z1 равно отношению длин их начальных окружностей и называется передаточным числом u 12, которое равно
u 12= z2 / z1=2p ∙r w2 / 2p ∙r w1 = r w2 / r w1. (2.77)
Номинальные передаточные числа цилиндрической зубчатой передачи u относятся к основным параметрам и регламентируются ГОСТ 2185 – 66.
Дискретная величина передаточного числа не всегда совпадает с аналоговым значением передаточного отношения
u 12= z 2/ z 1 = w ¢1/ w ¢2 = i¢ 12, (2.78)
где w ¢1 и w ¢2 – фактические значения угловых скоростей колес 1 и 2;
i¢ 12– скорректированное значение передаточного отношения пары колес.
Постоянство передаточного отношения обеспечивается формой взаимодействующих профилей зубьев колес 1 и 2. В основу их построения положено требование неизменности положения полюса зацепления по отношению к центрам вращения колес.
Распространение получили передачи с эвольвентным профилем.
Коэффициент полезного действия цилиндрической передачи
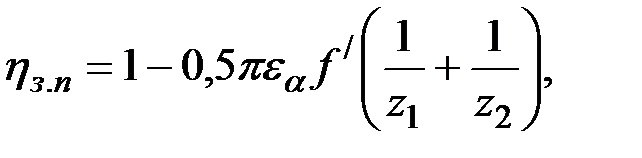(2.79)
где f / – коэффициент трения (f / = 0,06…0,1), принимаем f / = 0,1;
εα – коэффициент торцового перекрытия.
Цилиндричекие передачи являются основой цилиндрических редукторов.
Цилиндрический зубчатый редуктор – устройство, которое входит в состав привода машины и предназначено для передачи вращательного движения с понижением его кинематических характеристик от входа к выходу.
|
|
Передаточная функция редуктора выражается передаточным отношением, которое устанавливает параметры понижения кинематических характеристик
iр = wвх/wвых = nвх/n вых , (2.80)
где nвх , nвых, об/мин– частоты вращения входного и выходного валов редуктора, соответственно; wвх и wвых, рад /с – угловые скорости входного и выходного валов редуктора, соответственно.
В зубчатых передачах передаточное отношение i отождествляется с передаточным числом u, которое представляет собой соотношение числа зубьев сопряженных колес и в понижающей передаче равно
u = z 2/ z 1 (2.81)
где z 1– число зубьев ведущего колеса; z 2– число зубьев ведомого колеса.
В случае, когда кинематическая схема редуктора состоит из последовательно соединенных k передач, общее передаточное число определяется произведением передаточных чисел всех ступеней редуктора
u р= u 1× u 2×… × u k (2.82)
где u 1, u 2,…, u k передаточные числа 1-ой, 2-ой,…, k -ой ступени редуктора.
Номинальные значения передаточных чисел u для одно – и много-ступенчатых цилиндрических редукторов устанавливает ГОСТ 25301 – 95.
Частота вращения n 1, n 2, …, n k последовательно рассмотренных валов редуктора определяется соотношениями:
n 1= nвх; n 2= n1 / u 1; …; n k= n k-1 / u к. (2.83)
Угловые скорости w 1, w 2,… w k,соответственно, равны
w 1= wвх; w2=w1/u1; …; wk= wk-1 /uк. (2.84)
Мощность Р, кВт, на каждом последующем валу равна
Р 1= Рвх; Р 2= Р 1×h1; …; Р k= Р k-1×hk-1, (2.85)
где Р1, Р2 ,…, Рk – мощность на 1-ой, 2-ой,…, k-ой ступени редуктора;
h1 , h1 ,…,hk-1 –коэффициенты полезного действия 1-ой, 2-ой,…,(k-1)-ой ступени, показывающие какая часть подводимой энергии к каждой передаче используется полезно.
|
|
Вращающие моменты T1, T2, … Tk, Н×м на каждом последующем валу равны, соответственно:
T1 =103∙ Р 1/ w1; T2 =103∙ Р 2/ w2; …; Tk =103∙ Р k/ wk. (2.86)
Основные размеры концов валов и допускаемые крутящие моменты для цилиндрических редукторов устанавливает ГОСТ 24266 – 94.
Номинальные значения межосевых расстояний для одно и – мно-гоступенчатых редукторов устанавливает ГОСТ 25301 – 95. При этом использованы рекомендации ГОСТа 2185 – 66 «Передачи зубчатые цилиндрические».
Распространение получили редукторы с эвольвентными цилиндрическими зубчатыми передачами.
Форму и размеры зубьев передач зубчатых цилиндрических эвольвентных устанавливает ГОСТ 13755 – 2015 «Передачи зубчатые цилиндрические эвольвентные. Исходный контур».
Расчет геометрии зубчатых цилиндрических эвольвентных передач внешнего зацепления выполняется в соответствии с ГОСТ 16532 – 70.
На рисунке 2.25 представлена кинематическая схема двухступенчатого цилиндрического редуктора.
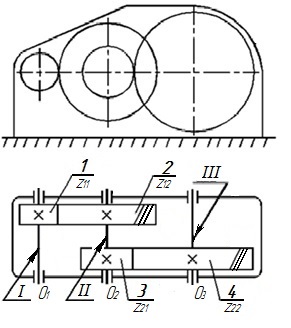
Рисунок 2.25 – Кинематическая схема цилиндрического двухступенчатого редуктора:1, 2, 3, 4 – колеса с числом зубьев z11, z12, z21 и z22, соответственно; I, II, III – валы редуктора; О1, О2, О3 – опоры валов
Широкое распространение цилиндрических редукторов обусловлено их достоинствами: большая долговечность и надежность работы; высокий К.П.Д.; постоянство передаточного числа; большой диапазон передаваемых мощностей; компактность; небольшие нагрузки на валы и опоры передачи.
К недостаткам относятся: шум при больших скоростях; относительно большая металлоемкость; высокая жесткость, не позволяющая компенсировать динамические нагрузки; невозможность бесступенчатого изменения передаточного числа.
Наибольшее распространение для передач общего назначения получили стали марок: 35, 40, 45, 50, 40Х, 35ХМ, 50ХН, 50Г и другие, с использованием объемной или поверхностной закалки. Для передач, работающих с частыми переключениями, перегрузками и ударами, когда наряду с высокой твердостью рабочих поверхностей требуется достаточная пластичность сердцевины и противоударная стойкость зубьев, целесообразно применять стали 15Х, 20Х, 20ХНМ, 18ХГТ и т.п. с последующей цементацией и термообработкой. Для колес больших размеров применяются углеродистые и низколегированные стали в нормализованном состоянии. Нередко такие колеса изготавливаются литьем из сталей 40Л, 45Л, 50Л или 40ХЛ, 30ХГСЛ и т.п.
Для изготовления средненагруженных тихоходных зубчатых колес больших размеров, не испытывающих ударных нагрузок, целесообразно использование модифицированных чугунов повышенной прочности.
Корпусные детали редукторов чаще выполняют литыми из чугуна СЧ 15 или алюминиевого сплава АЛ11. Наиболее распространена для цилиндрических редукторов конструкция корпусных деталей с разъемом по плоскости, в которой лежат продольные оси валов.
Форму корпуса и крышки образуют вертикальные, горизонтальные и наклонные (на крышке) поверхности с минимальным числом дополнительных элементов: строповочных «ушек», полок для болтов и штифтов, соединяющих крышку и корпус, а также бобышек под подшипниковые узлы, смотровые окна, отверстия для заливки и слива масла или его принудительной подачи, маслоуказатели и отдушины.
Для создания необходимой жесткости наружная поверхность стенок корпуса редуктора снабжается ребрами жесткости, а присоединительные поверхности корпуса и крышки изготовляют в виде достаточно широких горизонтальных полок, которые пересекаются с поверхностями бобышек подшипниковых узлов. Днище корпуса выполняется с уклоном в сторону сливного отверстия или двухскатным с уклоном к оси симметрии (для полного слива масла).
На валах редуктора чаще устанавливаются конические роликоподшипники, воспринимающие значительные радиальные и осевые нагрузки.
Нагрузки, возникающие в зоне контакта, могут вызывать повреждение поверхности и (или) разрушения структуры материала, из которого изготовлен элемент. Ответственной за напряженно - деформированное состояние контактирующих поверхностей является сила Fn вблизи полюсной линии, которая вызывает контактные напряжения и напряжения изгиба. Равнодействующая F n всех удельных сил, действующих по линии контакта в плоскости зацепления, действует по нормали к профилю зуба. Составляющая нормальной силы F n, которая направлена по касательной к начальным поверхностям элементов зацепления, называется окружной силой F t. Окружная сила присутствует во всех видах цилиндрических передач вращения. Составляющая нормальной силы F n, которая направлена к центру вращения колес передачи называется радиальной силой F r. Радиальная сила также присутствует во всех видах цилиндрических передач вращения. Составляющая нормальной силы F n, которая направлена вдоль оси вращения элементов передачи, называется осевой силой F х. Осевая сила присутствует во всех видах передач, кроме прямозубой цилиндрической. Схема сил, действующих в цилиндрической передаче с эвольвентным профилем зуба в зацеплении показана на рисунке 2.26.
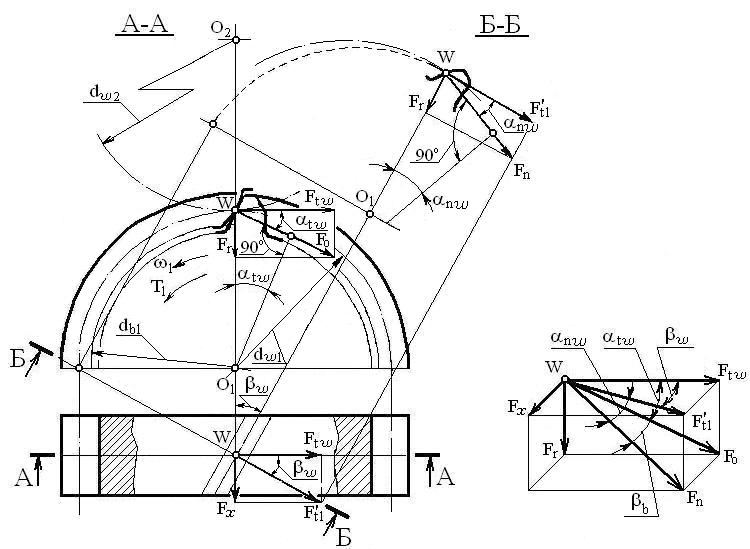
Рисунок 2.25 – Силы в зацеплении цилиндрических колес с эвольвентным
профилем зуба
Окружная составляющая F tw (Н) нормальной силы F n (Н) на начальном цилиндре диаметром d w (мм)
F tw=2×103× Т / d w, (2.87)
где Т - вращающий момент, Н×м.
Радиальная составляющая F r(Н) нормальной силы F n (Н)
F r= F tw× tg atw, (2.88)
где a tw угол зацепления передачи в торцовом сечении.
Осевая составляющая F х (Н) нормальной силы F n (Н)
F х = F tw× tg b w, (2.89)
где b w – угол наклона линии зуба на начальном цилиндре.
Нормальная сила F n (Н)
F n =2× Т /(d × cos at × cos b b) = F tw/(cos atw × cos b b), (2.90)
где b b – угол наклона линии зуба на основном цилиндре.
Нормальная к зубу нагрузка F n передается по контактным линиям общей длиной lå, зависящей от рабочего венца колес bw и угла наклона линии зуба b.
Нормальную силу Fn, приходящуюся на единицу длины контактной линии l, называют удельной нагрузкой w m.
w m = F n/ l. (2.91)
Удельная нагрузка с учетом корректирующих коэффициентов (режима нагруже-ния, неравномерности распределения нагрузки, динамического влияния и т.п.), устанавливаемых по критериям работоспособности определяют рабочую нагрузку.
В расчетах оценивают нагрузку, которая вызывает наибольшее опасное напряжение для данного вида повреждения. Расчет нагрузок, изменяющихся во времени, производят по ГОСТ 21354 – 87 одним из нижеприведенных методов:
- метод эквивалентных циклов, который ориентирован на приведение переменной нагрузки к величинам, вызывающим наибольшее повреждение элементов передачи;
- м етод эквивалентных моментов, который предусматривает, что эквивалентный момент учитывает значение и длительность всех уровней нагрузки;
- м етод эквивалентных напряжений, которыйоснован на определении расчетного напряжения для каждой ступени нагружения.
Под действием внешних нагрузок в материале зуба передачи вознникают напряжения, оценка которых позволяет оценить работоспособность конструкции.
В полюсе зацепления опасными являются контактные напряжения.
Контактное напряжение sН (МПа), в основу расчета которых положено решение задачи о напряженном состоянии статически сжатых цилиндрических тел с учетом теории Герца. Контактное напряжение в полюсе зацепления равно
sН =sН0×(К Н)1/2, (2.92)
где sН0 – контактное напряжение без учета дополнительных нагрузок, МПа; К Н – коэффициент неравномерности распределения нагрузки.
Коэффициент нагрузки К Н
К Н = К А× К Нv × К Нb × К Нa, (2.93)
где К А – коэффициент, учитывающий внешнюю динамическую нагрузку;
К Нv – коэффициент, учитывающий внутреннюю динамическую нагрузку;
К Нb – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; К Нa – коэффициент, учитывающий распределение нагрузки между зубьями.
Величину контактного напряжения sН0 (МПа) в зависимости от: окружного усилия F t (Н) на делительном цилиндре в торцовом сечении, делительного диаметра d 1 (мм) ведущего элемента, рабочей ширины bw (мм) венца контактирующих элементов и передаточного числа устанавливают по следующей зависимости
sН0=ZE×ZH×Ze×Zb×[ F t×(u +1)/(bw× d 1× u)]1/2, (2.94)
где ZE – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес
ZЕ ={Eпр/[p×(1– m2)]}1/2; (2.95)
ZH – коэффициент, учитывающий форму сопряженных поверхностей зубьев в полюсе зацепления (влияние радиусов кривизны боковых поверхностей и переход от окружной силы на делительном цилиндре на нормальную на начальном цилиндре)
Z Н =(1/ cos at)×(2× cos b b / sin aw)1/2; (2.96)
Ze – коэффициент, учитывающий суммарную длину контактных линий
Z e=(1/ e a)1/2; (2.97)
Zb –коэффициент, учитывающий наклон зуба.
Допускаемое контактное напряжение sНР (МПа) не вызывающее опасной контактной усталости материала при минимальном запасе прочности SHmin,
sНР =sНlim× ZL×ZR×Zv×Zw×ZX/SHmin, (2.98)
где sНlim – предел контактной выносливости поверхностей зубьев, соответствующий эквивалентному числу циклов напряжений, МПа; ZL – коэффициент, учитывающий влияние вязкости смазочного материала; ZR – коэффициент, учитывающий влияние шероховатости сопряженных поверхностей зубьев; Zv– коэффициент, учитывающий влияние окружной скорости; Zw – коэффициент, учитывающий влияние перепада твердостей материалов сопряженных поверхностей зубьев (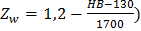
; ZX – коэффициент, учитывающий размер зубчатого колеса.
Предел контактной выносливости sНlim (МПа) равен
sНlim=sНlimb ×ZN, (2.99)
где sНlimb – предел контактной выносливости, соответствующий базовому числу циклов напряжений, МПа; ZN – коэффициент долговечности. Коэффициент долговечности ZN
ZN =(N Hlim/ N К)1/q, (2.100)
где N Hlim – базовое число циклов перемены напряжений, соответствующее пределу выносливости при контактных напряжениях; N К –суммарное число циклов напряжений за весь срок службы (при использовании метода эквивалентных циклов вместо N К подставляют N НЕ); q – показатель степени кривой выносливости при контактных напряжениях.
Допускаемое предельное контактное напряжение (sНРmax), не вызывающее остаточной деформации или хрупкого разрушения поверхностного слоя
sНPmax =sНSt/ S НStmin, (2.101)
где sНSt – предельное контактное напряжение при действии максимальной (пиковой) нагрузки; SНStmin – минимальный коэффициент запаса прочности по максимальным контактным нагрузкам.
Нагрузочная способность поверхности зубьев обеспечивается при выполнении любого из критериев:
- критерия напряжений
sН £sНP, (2.102)
sНmax £sНРmax; (2.103)
- критерия безопасности
SН³ SНmin, (2.104)
SНSt³ SНStmin; (2.105)
- критерия ресурса
NL³ NK, (2.106)
sНmax £sНРmax; (2.107)
- критерия вероятности безотказной работы
Р Н(NL ³ NK)³ Р Нmin, (2.108)
Р НSt(sНSt³sНmax)³ Р НStmin. (2.109)
В этих формулах SН – расчетный коэффициент запаса прочности для предотвращения опасной контактной усталости; SНSt – расчетный коэффициент запаса прочности для предотвращения опасных разрушений поверхностного слоя при максимальной нагрузке; sНmax – максимальное контактное напряжение за весь срок службы; NL – число циклов напряжений в соответствии с расчетным сроком службы; NK – число циклов напряжений в соответствии с заданным сроком службы; Р Н – вероятность безотказной работы в течении заданного срока службы; Р Нmin – минимальное регламентированное значение Р Н; Р НSt – вероятность безотказной работы при расчете по максимальным контактным нагрузкам;
Р НStmin – минимальное регламентированное значение Р НSt.
На переходной поверхности контактирующих элементов опасным является напряжение изгиба sF (МПа), которые зависят от окружной силы F t (Н) на делительном диаметре (в торцовом сечении), ширины bw (мм) венца зубчатого колеса и нормального модуля m n.
Напряжение изгиба устанавливают по формуле
sF = F t× K F×YFS×Yb×Ye/(bw× m n), (2.110)
где YFS – коэффициент, учитывающий форму зуба и концентрацию напряжений (зависит от количества зубьев на колесе и величины смещения инструмента при нарезании зуба); Y b – коэффициент, учитывающий влияние угла наклона зуба; Ye – коэффициент, учитывающий влияния перекрытия зубьев; K F – коэффициент нагрузки.
Коэффициент нагрузки
K F = К А× К Fv × К Fb × К Fa, (2.111)
где К А – коэффициент, учитывающий внешнюю динамическую нагрузку; К Fv – коэффициент, учитывающий внутреннюю динамическую нагрузку; К Fb – коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий; К Fa – коэффициент, учитывающий распределение нагрузки между зубьями.
Допускаемое напряжение изгиба sFР (МПа) на переходной поверхности, не вызывающее усталостного разрушения материала при минимальном коэффициенте запаса прочности SFmin
sFР =sFlimb×YN×YR×YX×Yd/SFmin, (2.112)
где sFlimb – предел выносливости зубьев при изгибе, МПа; YN – коэффициент долговечности; YR – коэффициент, учитывающий влияние шероховатости переходной поверхности; YX – коэффициент, учитывающий размер колеса; Yd –коэффициент, учитывающий чувствительность материала к концентрации напряжений и градиенту напряжений (опорный коэффициент).
Предел выносливости зубьев при изгибе sFlimb
sFlimb =s0Flimb× К, (2.113)
где s0Flimb – предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений, МПа; К – коэффициент, учитывающий технологию изготовления, способ получения заготовки, влияние шлифования, деформационного упрочнения и реверсивность (при одностороннем приложении нагрузки К »1).
Коэффициент долговечности YN
YN =(N Flim/ N К)1/q, (2.114)
где N Fhlim – базовое число циклов перемены напряжений, соответствующее пределу выносливости материала при изгибе; N К – суммарное число циклов напряжений за весь срок службы (при использовании метода эквивалентных циклов вместо N К подставляют N FЕ).
Фактические значения контактных напряжений и напряжений изгиба не должны превышать допускаемых величин, что является основанием для установления геометрических параметров передачи.
Проектный расчет закрытых передач ведут по допускаемым контактным напряжениям с последующей проверкой по напряжениям изгиба. Расчет открытых передач производят по допускаемым напряжениям с последующей проверкой по контактным напряжениям. Допускаемое напряжение изгиба в опасном сечении (sFрmax), не вызывающее остаточной деформации, хрупкого излома или первичных трещин равно
sFpmax =(sFSt/SFstmin)×(YdSt/YdStT), (2.115)
где sFSt – предельное напряжение изгиба при действии максимальной
нагрузке; SFstmin – минимальный коэффициент запаса прочности по максимальным нагрузкам; YdSt – опорный коэффициент при максимальной нагрузке; YdStT – опорный коэффициент испытываемого зубчатого колеса при максимальной нагрузке.
Нагрузочная способность зуба при изгибе обеспечивается при выполнении любого из критериев:
- критерия напряжений
sF £sFP, (2.116)
sFmax £sFрmax; (2.117)
- критерия безопасности
SF³ SFmin, (2.118)
SFSt³ SFStmin; (2.119)
- критерия ресурса
NL³ NK, (2.120)
sFmax £sFРmax; (2.121)
- критерия вероятности безотказной работы
Р F (NL³ NK)³ Р Fmin, (2.122)
Р FSt(sFSt³sFmax) ³ Р FStmin. (2.123)
В этих формулах SF–расчетный коэффициент запаса прочности для предотвращения усталостного разрушения материала; SFSt – расчетный коэффициент запаса прочности для предотвращения опасных повреждений при максимальной нагрузке; sFmax – максимальное местное напряжение от изгиба в опасном сечении за весь срок службы; NL – число циклов напряжений в соответствии с расчетным сроком службы; NK – число циклов напряжений в соответствии с заданным сроком службы; Р F – вероятность отсутствия повреждений в течении заданного срока службы; F Нmin – минимальное регламентированное значение Р F; Р FSt – вероятность отсутствия хрупкого излома или остаточной деформации при максимальной нагрузке; Р FStmin –минимальное регламентированное значение Р FSt