Математическая модель асинхронного двигателя во вращающейся ортогональной системе координат, ориентированной по потокосцеплению ротора

АД имеет трехфазную обмотку на статоре и короткозамкнутую обмотку на роторе. Его принцип действия основан на том, что вращающееся магнитное поле статора, пересекая проводники обмотки ротора, наводит в них напряжение, вызывающее протекание тока в обмотке ротора. Взаимодействие этого тока с потоком статора создает электромагнитный момент, приводящий ротор во вращение. Из этого видно, что для создания момента, вращающего ротор, необходимо, чтобы электрическая частота (скорость) вращения ротора ω_r была бы меньше частоты вращения магнитного потока статора ω_s, причем ω_r=Z_p ω, где ω – механическая скорость вращения ротора, Z_p – число пар полюсов двигателя. Величина Δω=ω_s-ω_r называется абсолютным скольжением двигателя, а величина s=(ω_s-ω_r)/ω_sb – относительным скольжением, где ω_sb – номинальная электрическая частота питания статора (обычно ω_sb=314 1/сек).

Схема замещения двигателя изображена на рис.6.

Рисунок 6 – Схема замещения АД

АД представляет собой нелинейный многомерный объект с достаточно сложной структурой. При его математическом описании большое значение имеет корректность принятых в каждом конкретном случае допущений. Разнообразие математических моделей АД связано с содержанием сделанных допущений, с системой координат, в которых выполнено математическое описание, с содержанием входных и выходных сигналов модели и с системой принятых относительных величин.

В зависимости от принятой системы координат разработаны следующие модели АД:

· модели АД в трехфазной системе координат;

· модели АД в двухфазных ортогональных системах координат;

· однофазные модели на основании статических характеристик АД с упрощенным учетом электромагнитных процессов (на основании схемы замещения АД в установившемся режиме).

Выбор системы координат и конфигурации модели, т.е. состава входных и выходных сигналов, зависит от структуры системы управления, в частности, от состава сигналов, с помощью которых организуются обратные связи, и от особенностей источника питания двигателя.

Удачный выбор математической модели является важным не только при анализе, но и при синтезе системы автоматического управления. Именно разработка модели в системе координат, ориентированной по потокосцеплению ротора, стала основой создания высококачественных систем векторного управления.

Для перехода от математического описания гармонических сигналов в многофазовых координатах к математическому описанию в ортогональных двухфазных координатах используется понятие обобщенного вектора.

Обобщенным называют такой вектор , проекции которого на оси фаз равны мгновенным значениям соответствующих фазных величин в заданный момент времени.

Для выполнения этой формулировки обобщенный вектор при угле поворота φ_к должен вращаться против часовой стрелки с угловой скоростью

, (1)

совпадающей с угловой скоростью соответствующего периодического сигнала и иметь модуль, который равен максимальному значению фазной величины

. (2)

Рисунок 7 – Обобщенный вектор и его составляющие

На рис.7 изображен обобщенный вектор какой-либо физической величины ротора , его проекции на физические оси векторная сумма этих проекций и проекции обобщенного вектора на действительную d (Re) и мнимую q (Im) оси, первая из которых (v_d) совпадает с осью А, а вторая (v_q) – расположена перпендикулярно к первой и повернута на угол 90˚ против часовой стрелки.

В литературе [4], [5] показано, что сумма векторов представляет собой вектор, который совпадает с обобщенным вектором по направлению и превышает его амплитуду в 1,5 раза. С учетом этого можно записать:

, (3)

, (4)

где ; ; ;

,

а φ_νr – угол между направлением обобщенного вектора ротора и осью d:

.

Таким образом, формулы (3) и (4) описывают обобщенный вектор ротора в трехфазной (abc) и ортогональной (dq) системах координат, которые вращаются со скоростью

, .

Для того, чтобы направление действительной оси ортогональной системы координат совпадало с направлением обобщенного вектора потокосцепления ротора ψ_r, взятого за основу, система координат должна вращаться синхронно с этим вектором. При этом вектор потокосцепления ротора в ней будет иметь только действительную составляющую, так как проекция этого вектора на мнимую ось q будет равна нулю. Тогда условия математического описания АД в этих координатах будут иметь вид

, (5)

; . (6)

Модель в системе координат dq стала основой разработки системы векторного управления короткозамкнутым АД. Поэтому в дополнение к условиям (5), (6) добавим условие равенства нулю напряжения ротора

. (7)

При питании обмоток статора двигателя от источника напряжения система векторного управления имеет обратные связи по составляющим тока статора и по потокосцепления ротора. Поэтому еще одним условием для разработки модели АД будет наличие в ней перечисленных сигналов: i_sd, i_sq, ψ_r.

Запишем уравнения, описывающие процессы в АД, в обобщенных векторах с учетом условия (7):

(8)

где ω_к – частота вращения системы координат;

ω_r – электрическая частота вращения ротора;

U_s, i_s – напряжение и ток статора;

R_s – сопротивление обмотки статора;

i_r – ток обмотки ротора;

R’_r – приведенное сопротивление обмотки ротора;

Ψ_r – потокосцепление ротора.

Для короткозамкнутого двигателя векторы отличаются друг от друга из-за наличия рассеяния обмоток статора и ротора. В этой связи для них можно записать:

(9)

где L_m – главная индуктивность рассеяния;

L_sl, L_rl – индуктивность рассеяния обмоток.

При этом для индуктивностей обмоток статора L_s и ротора L_r будем иметь:

(10)

Для того, чтобы обеспечить оговоренный ранее состав сигналов модели, найдем обобщенные вектора тока ротора и потокосцепления статора:

; (11)

, (12)

где ; .

После подстановки уравнений (11), (12) в систему уравнений (8) получим:

(13)

где электромагнитная постоянная времени

.

Для того, чтобы первое уравнение системы (13) имело производную только от одного сигнала, выразим производную от потокосцепления ротора во втором уравнении.той же системы и подставим полученное выражение в первое:

(14)

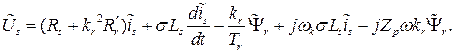(15)

Перепишем (14) и (15) с учетом их проекций на оси d и q. Получим следующую систему

(16)

Обозначим

,

и перепишем дифференциальное уравнение (16) в операторной форме:

(17)

В последнем уравнении системы (17) обозначим:

(18)

- скорость ротора и абсолютное скольжение, приведенные к скорости электромагнитного поля.

Уравнение для электромагнитного момента двигателя представляется как [4], [6]:

. (19)

При этом уравнение механического равновесия запишется в обычном виде:

,

где J – приведенный момент инерции электропривода.

По полученным выше уравнениям в пакете Matlab составим модель короткозамкнутого АД. Она приведена на рис.8, с учетом того, что L_sl=σL_s

Приведенная структурная схема может быть использована при исследовании асинхронного электропривода с системой векторного управления при управлении по потокосцеплению ротора. Модель имеет два линейных канала управления, что значительно упрощает синтез передаточных функций регуляторов. При этом в системе управления в зависимости от параметров двигателя должны быть скомпенсированы внутренние перекрестные обратные связи с воздействиями U_kd и U_kq.

 

 

Рисунок 8 – Структурная схема АД с КЗ ротором во вращающейся системе координат, ориентированной по потокосцеплению ротора.

На рис.8 обозначено: U_kd – напряжение перекрестной связи по каналу реактивного тока (для компенсации);

U_kq – напряжение перекрестной связи по каналу активного тока (для компенсации).

1.3.1 Модель в системе координат α, β

Система координат α, β применяется для анализа систем электропривода с управлением двигательными и тормозными режимами асинхронных машин по цепи статора, в том числе при анализе систем с векторным управлением и для исследования режимов при несимметрии статорных цепей.

Определенную сложность при построении модели АД в системе координат α, β представляет то обстоятельство, что эквивалентные напряжения и изменяются во времени по синусоидальному закону с постоянной частотой источника электроэнергии ω_0эл = 2p f _с, рад/с.

Структурная схема для моделирования соответствующих напряжений статора представлена на рисунке 3.5.

Рисунок 9 – Схема задания напряжения статора

 

Уравнения электрического равновесия в осях a, b принимают вид [2]:

(20)

Рисунок10 - Структурные схемы АД в системах координат α, β

1.3.2. Модель в системе координат x,y

 

Систему координат x, y используют преимущественно для исследования режимов синхронных и асинхронных машин при несимметрии ротора. Она наиболее целесообразна при расчете систем электропривода с машинами двойного питания, например, каскадных схем управления АД с фазным ротором. При этом статорные и роторные переменные изменяются по синусоидальному закону с частотой скольжения двигателя.

В синхронных машинах в статических режимах работы w_0.эл = w_эл, поэтому использование системы координат x, y позволяет оперировать соотношениями, аналогичными постоянному току.

Выбор w _k = w_эл = ω _r соответствует преобразованию реальных переменных машины к осям x, y, жестко связанным с ротором машины. При таком преобразовании напряжения и токи являются переменными величинами, но имеют как в роторной, так и в статорной обмотке частоту тока ротора w _{r .эл} = w_0.эл - w_эл. Проекции вектора напряжения на координатные оси x и y определяются выражениями:

, . (21)

На рис. 3.6 изображена структурная схема формирования питающих напряжений обмоток статора и :

Рисунок 11 – Структурная схема модели источника синусоидального

напряжения переменной частоты

 

Уравнения электрического равновесия в осях x, y принимают вид:

(22)

Потокосцепления обмоток определяются результирующим действием токов всех обмоток статора и ротора:

, (23)

Из уравнения (3.8) определим токи обмоток статора и ротора:

(24)

И в итоге получаем:

, (25)

Рисунок12 - Структурные схемы АД в системах координат x, y

 

1.3.3. Модель в системе координат d, q

 

Третью систему координат d, q целесообразно использовать только для исследования симметричных режимов асинхронных машин, если ее применение приводит к упрощению описаний возмущающих воздействий.

Модели d,q, также как и x,y, привязаны к скорости поля статора (или ротора), что ограничивает область их применения только случаями питания статора АД синусоидальнымнапряжением.

питания, что во много раз усложняет расчет.

Выбор w _k = w_0.эл, позволяет осуществить преобразование к осям d, q, вращающимся с синхронной скоростью поля машины. При этом уравнения электрического равновесия записываются так [1,2]:

(26)

К реальным обмоткам статора приложена симметричная двухфазная система напряжений. При ω _k = ω_0эл и φ _k = ω_0эл t выражения для напряжений имеют вид:

(27)

Таким образом получаем:

(28)

Рисунок12 - Структурные схемы АД в системах координат d, q
2 Расчет параметров двигателя и регуляторов