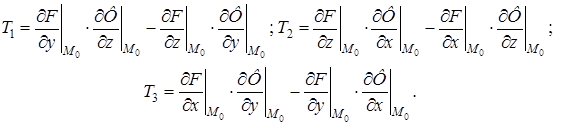ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО
ИСЧИСЛЕНИЯ
ПЛАН ЛЕКЦИИ
I. Поверхности. Касательная плоскость и нормаль
II. Пространственные линии
III. Линия как пересечение двух поверхностей
I. Поверхности. Касательная плоскость и нормаль. Если уравнение поверхности в пространстве имеет вид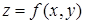 
, то уравнением касательной плоскости к поверхности в точке 
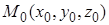служит
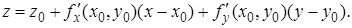(1)
Рассмотрим в пространстве 
поверхность S, заданную уравнением общего вида
.
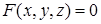Предположим, что функция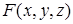 
в окрестности точки 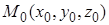удовлетворяет условиям теоремы существования неявной функции и уравнение 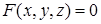определяет z как функцию x и y, то есть 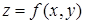, причем, 
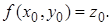Производные этой функции в точке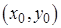 
, 
.
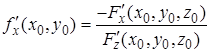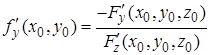Уравнение касательной плоскости можно переписать в виде
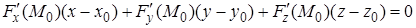
или
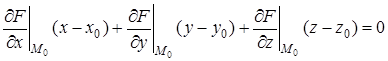. (2)
Определение. Прямая, перпендикулярная к касательной плоскости в точке касания, называется нормалью к поверхности в этой точке.
 |
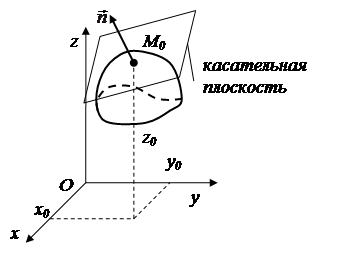Уравнение нормали к касательной плоскости в точке касания имеет вид
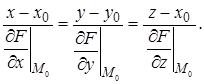
Если поверхность задана уравнением 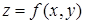, то уравнение нормали к этой поверхности в точке :
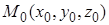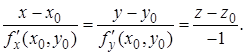(3)
Пример. Написать уравнение касательной плоскости и нормали к поверхности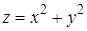 
(параболоид) в точке 
.
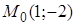Решение. Найдем значение функции в точке :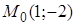 
.
Запишем частные производные функции z: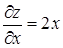 
и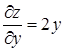 
и вычислим их значения в точке 
: 
, 
.
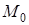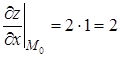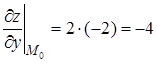Запишем уравнение касательной плоскости (1)
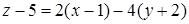
или после преобразований
.
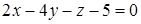Уравнение нормали к поверхности в точке М0 запишем, воспользовавшись формулой (3):
.
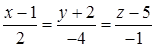II. Пространственные линии. Линия, принадлежащая пространству 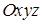, может быть задана параметрическими уравнениями
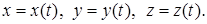(4)
Если все три уравнения линейные, то получаются известные из аналитической геометрии параметрические уравнения прямой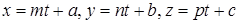 
. Исключая из этих уравнений параметр t, получим канонические уравнения прямой 
Касательная к пространственной кривой определяется так же, как и для плоской кривой, то есть как предельное положение секущей, проходящей через данную точку 
и близкую к ней точку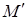 
при условии, что 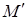стремится слиться с точкой .
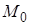Получим уравнение касательной к линии, заданной параметрическими уравнениями (4), в точке линии 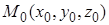, соответствующей значению параметра 
.
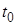Уравнение секущей прямой, проходящей через точк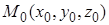и и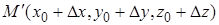 
, будет
.
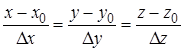Делим все знаменатели на D t и переходим к пределу при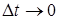 
. Тогда получим искомое уравнение касательной
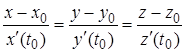, (5)
где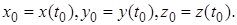 
Направляющие косинусы касательной в точке 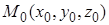выражаются формулами
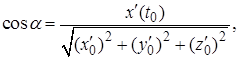
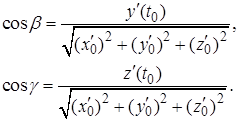
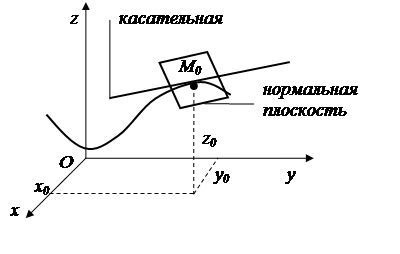
Прямая, перпендикулярная к касательной и проходящая через точку касания, называется нормалью к линии в данной точке. Линия в точке имеет бесконечное множество нормалей. Все они лежат в одной плоскости, перпендикулярной к касательной прямой и проходящей через точку касания.
Определение. Плоскость, перпендикулярная к касательной к кривой в точке касания, называется нормальной плоскостью к кривой в данной точке.
Уравнение нормальной плоскости в точке касания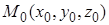
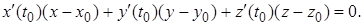(6)
 |
III. Линия как пересечение двух поверхностей. Кривая в пространстве может быть задана и как линия пересечения двух поверхностей: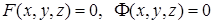 
.
Геометрически ясно, что касательной к этой линии в точке M0 будет линия пересечения касательных плоскостей к данным поверхностям в этой же точке. Составляя уравнения этих плоскостей в соответствии с соотношением (2),
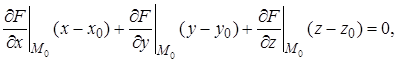
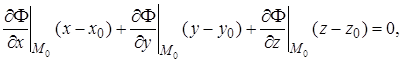
получим уравнение искомой касательной как линии пересечения двух плоскостей. Направляющий вектор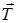 
этой касательной можно найти, взяв векторное произведение нормальных векторов к обеим плоскостям
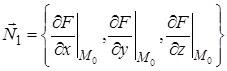
и
.
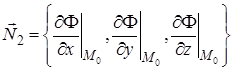Тогда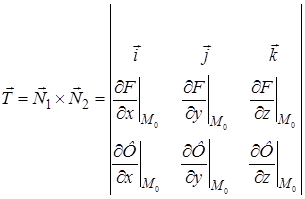 
.
Зная направляющий вектор 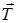и точку касания 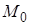, можно переписать уравнение касательной в каноническом виде, а также составить уравнение нормальной плоскост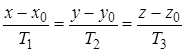и:
и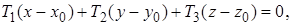 
где 