Взаимные преобразования автоматов

Общие положения

Конечный автомат - это набор из пяти элементов ,

где - алфавит внутренних состояний;

- входной алфавит (алфавит входных символов);

- выходной алфавит (алфавит выходных символов);

d - функция переходов из состояния в состояние;

l - функция выходов.

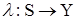В теории автоматов наиболее часто рассматриваются автоматы Мили и Мура, у которых функции переходов имеют одинаковый вид (), а функции выходов существенно различны ( для автомата Мили и для автомата Мура), что определяет разное поведение автоматов. При этом решают задачи анализа и синтеза автоматов, их взаимных преобразований, установление эквива-лентности автоматов и др.

Представление автомата

Для описания работы автомата чаще всего используют таблицы и графы переходов. В табл. 4.1 приведен пример представления автомата Мили, а в табл. 4.2 - автомата Мура.

Таблица 4.1

		...
		...
...	...	...	...
		...

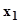
Таблица 4.2

		...
		...
...	...	...	...
		...

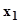
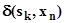
Автомат называется полностью определённым, если множество пар для функций перехода и выхода равны множеству пар 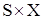. У частично определённого автомата функции d и l определены на множестве не всех пар ; в этом случае некоторые клетки не заполнены.

Граф переходов строится следующим образом. Две вершины и (исходное состояние и состояние перехода) соединяются дугой, направленной от к , если в автомате имеется переход из в (если 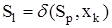). Для автомата Мили дуге (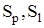) приписывается входной символ 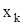и выходной . Для автомата Мура входной символ записывается внутри вершины или рядом с ней, а дуге приписывается только входной символ .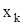

Пример 4.1. Автомат Мили задан таблично (табл. 4.3) и графически (рис. 4.1).

Таблица 4.3

РРис. 4.1. Граф автомата А₁

Пример 4.2. Автомат Мура задан таблично (табл. 4.4) и графически (рис. 4.2).

Таблица 4.4

Рис. 4.2. Граф автомата А₂

Взаимные преобразования автоматов

Одной из основных задач, решаемых в теории автоматов, является задача эквивалентного преобразования автомата Мили в автомат Мура либо наоборот.

Рассмотрим связь между автоматами Мили и Мура. Два автомата и 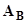с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установления их в начальной состояния их реакции на любое входное слово совпадают. Для любого автомата Мили может быть построен эквивалентный ему автомат Мура и наоборот.

Преобразование автоматов связано с преобразованием их состоя-ний. На рис. 4.3 представлены преобразования для обоих случаев преобразования автоматов. Видно, что в случае а символы выхода на графе автомата Мура приписываются дуге на графе автомата Мили; в случае б в вершину s_m автомата Мура нельзя поместить несколько сим-волов выхода с дуг автомата Мили, поэтому такое состояние надо "расщеплять": S_m=(S'_m, S"_m), где S'_m=(s_m, y_n) S"_m=(s_m, y_p).

Аналогично поступают и при преобразованиях на таблицах.

а)

б)

Рис. 4.3. Преобразования автоматов (их состояний):

а) автомата Мура в автомат Мили; б) автомата Мили в автомат Мура

Пример 4.3. Рассмотрим преобразование автомата Мили А_А, заданного табл. 4.3 (графом на рис. 4.1) и алфавитами: 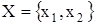, , 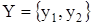, 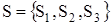в автомат Мура А_В. Для автомата А_В определим множество его состояний S_B и функцию выхода; этой информации достаточно для описания автомата А_В.

Состояние расщепляется в два состояния: и (обратите внимание на дуги, входящие в вершину, отождествляющую состояние S₁ и выходные буквы на них - ). Для удобства переобозначим их соответственно: 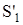и . Аналогично поступим и с другими состояниями. В результате получим:

Функции выхода автомата А_В определяются выражениями

Согласно схеме б (рис. 4.3) получим следующие переходы:

-из и переход в состояние ;

-из и переход в состояние ;

-из переход в состояние ;

-из переход в состояние ;

-из и переход в состояние ;

-из и переход в состояние ;

Табличное и графическое представления полученного автомата Мура А_В приведены в табл. 4.5 и на рис. 4.4.

Таблица 4.5

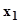
Рис. 4.4. Граф автомата Мура А_В

Пример 4.4. Рассмотрим преобразование автомата Мура А₂, задан-ный табл. 4.4, в автомат Мили A'₂. Поскольку оно простое, приведём готовый результат (табл. 4.6); граф можно построить самостоятельно.

Таблица 4.6
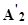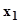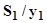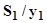