Определение момента инерции диска.
Проверка теоремы Штейнера
ЦЕЛЬ: определить момент инерции диска расчётным и экспериментальным методами
ОБОРУДОВАНИЕ: специальная установка, набор гирь, штангенциркуль, секундомер
Основные теоретические сведения
Работа, которую совершает постоянный момент силы M при повороте тела на угол j (в радианах),
А = Мj. (1)
Работа сил трения или сопротивления равна изменению механической энергии системы:
А = W 1– W 2. (2)
Кинетическая энергия тела массой m, которое движется поступательно со скоростью v и одновременно вращается с угловой скоростью w относительно центра масс,
 . (3)
. (3)
Эта энергия равна кинетической энергии вращательного движения относительно мгновенной оси (МОВ):
 . (4)
. (4)
В этих формулах I с – момент инерции тела относительно оси, проходящей через центр масс, I – момент инерции относительно МОВ.
Если эти оси параллельны друг другу, то согласно теореме Штейнера
 , (5)
, (5)
где m – масса тел, a – расстояние между осями.
Формулы для расчета моментов инерции некоторых тел относительно их оси симметрии приведены в табл. 1.
2.


 Описание установки
Описание установки
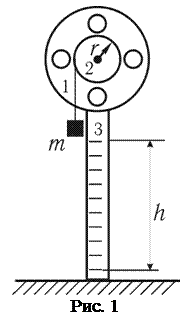
 Диск 1 с резьбовыми отверстиями насажен на ось (рис. 1) и может вращаться с малым трением. На той же оси находится шкив 2 радиусом r, на который наматывается нить. К другому концу нити привязан груз 4 массой m, под действием которого система приводится во вращение. Путь, пройденный грузом до своего нижнего положения (когда нить полностью размотается), определяется по шкале 3, вдоль которой груз движется.
Диск 1 с резьбовыми отверстиями насажен на ось (рис. 1) и может вращаться с малым трением. На той же оси находится шкив 2 радиусом r, на который наматывается нить. К другому концу нити привязан груз 4 массой m, под действием которого система приводится во вращение. Путь, пройденный грузом до своего нижнего положения (когда нить полностью размотается), определяется по шкале 3, вдоль которой груз движется.
В резьбовые отверстия диска могут вворачиваться дополнительные грузы 5 цилиндрической формы (радиуса R) и массы т 0.
В установках предусмотрено автоматическое измерение времени движения груза до нижней точки и расстояния h, на которое поднимается груз по инерции после прохождения нижнего положения.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
Если намотать нить на шкив, подняв на высоту h o груз m, то он будет обладать потенциальной энергией W о= mgh o. При падении груза его потенциальная энергия переходит в кинетическую энергию поступательного движения груза  и энергию вращения диска I w2/2. Зная время t падения груза до нижней точки, можно определить конечную скорость движения груза
и энергию вращения диска I w2/2. Зная время t падения груза до нижней точки, можно определить конечную скорость движения груза  и угловую скорость вращения диска
и угловую скорость вращения диска  , где r – радиус шкива.
, где r – радиус шкива.
При движении в подшипниках действует момент сил трения М тр, для преодоления которого на пути h 0 = j0 r совершается работа (см. (1))
 , (6)
, (6)
где jо – угол поворота диска (угловое перемещение), F тр – модуль силы трения.
В соответствии с законом сохранения энергии и равенством (2)
 . (7)
. (7)
Величину силы трения F тр найдём из следующих соображений. После того, как груз опустится до нижней точки, маховик, продолжая вращение по инерции, поднимет груз на высоту h; там его потенциальная энергия mgh меньше, чем начальная, на величину работы, совершенной против сил трения на всём пути h о+ h. Из закона сохранения энергии и формулы (2) следует
 . (8)
. (8)
Решая совместно уравнения (7), (8), получаем расчётную формулу для момента инерции вращающегося тела:
 . (9)
. (9)
Задание 1. Определение момента инерции диска
1. Снимите дополнительные грузы с диска.
2. Измерьте штангенциркулем диаметр шкива d в нескольких местах, записывая результаты в табл. 1, и определите среднее значение  .
.
Таблица 1
| №п.п. | d, м | t, с | h, м |  м
m = кг,
h 0= м м
m = кг,
h 0= м
|
| … | ||||
| Среднее значение | I д= кг×м2 |
3. Вращая диск, намотайте нить в один слой на шкив и включите электромагнит красной кнопкой, расположенной в верхней части установки. Измерьте и запишите расстояние h 0 от груза до нулевой отметки шкалы.
4. Определите массу груза m, подвешенного к нити, включите секундомер.
5. В момент прохождения грузом нижнего положениясекундомервыключается. Продолжая дальше наблюдение за движением груза m, заметьте высоту h, на которую поднимется груз, двигаясь по инерции. Показание секундомера t и высоту h запишите в табл. 1.
6. Повторите измерения еще четыре раза при тех же значениях m и h 0.
7. Вычислите среднее значение момента инерции диска IД по формуле (9).
З а д а н и е 2. Проверка теоремы Штейнера
1. Определите массу т о и радиус R дополнительных грузов. Закрепите их на одинаковом расстоянии от оси вращения на диске установки и замерьте расстояние l 1 от оси вращения до центра грузов. Результаты этих измерений и число дополнительных грузов k занесите в табл. 2.
Таблица 2
mo= кг
k=
R= м
r= м
ho= м
 Д =кг м2 Д =кг м2
| № п.п. |  м м
|  м м
|  м м
|  м м
| |||
 с с
|  м м
|  с с
|  м м
|  с с
|  м м
|  с с
|  м м
| |
| Среднее значение | ||||||||
| I эксп | ||||||||

| ||||||||

|
2. Занесите в табл. 2 результаты измерений, полученных в задании 1: радиус шкива r, массу груза т, расстояние, проходимое грузом до нулевой отметки h о, момент инерции диска I д и число дополнительных грузов k.
3. Проведите измерения (см. пп. 2-6 задания 1) и результаты занесите в табл.2.
4. Рассчитайте момент инерции I эксп диска с дополнительными грузами (формула 9).
5. Рассчитайте момент инерции дополнительных грузов I Г, используя теорему Штейнера  и результат занесите в табл.2.
и результат занесите в табл.2.
6. Рассчитайте момент инерции системы «диск–дополнительные грузы»  .
.
7. Проведите подобные измерения и расчеты с другим положением дополнительных грузов на диске (пп.3-6 задания 1).
8. Сравните полученное экспериментально значение момента инерции I экспи расчетное значение момента инерции системы I расч и сделайте выводы.
З а д а н и е 3. Оценка погрешности измерений
1. Оцените случайные погрешности измеряемых величин по разбросу полученных значений  и приборные (систематические) погрешности всех измерений. Результаты занесите в табл.3.
и приборные (систематические) погрешности всех измерений. Результаты занесите в табл.3.
Таблица 3
| Измеряемая величина | Погрешность | ||||
| системат. | случайная | наибольшая | |||
| название | средн. значение | ||||
| Масса груза т | кг | –– | |||
| Высота h o | м | –– | |||
| Высота h | м | ||||
| Время t | с | ||||
| Радиус r | мм | ||||
| Масса m o | г | –– | |||
| Радиус R | м | –– | |||
| Расстояние l | м | –– |
2. Относительную погрешность полученного результата  примите равной погрешности той величины, которая измерена менее точно и рассчитайте абсолютную погрешность величины момента инерции
примите равной погрешности той величины, которая измерена менее точно и рассчитайте абсолютную погрешность величины момента инерции
 .
.
Запишите результат в виде:
 .
.
3. Сравните расчетные значения момента инерции и полученные экспериментально и сделайте выводы.