Работа №5. Определение момента инерции тела, скатывающегося
С наклонной поверхности
ЦЕЛЬ: определить момент инерции тела относительно мгновенной оси вращения расчётным и экспериментальным методом
ОБОРУДОВАНИЕ: установка, набор тел, секундомер
ОПИСАНИЕ УСТАНОВКИ
 |
В работе используются тела, осью которых является цилиндрический стержень радиусом r. Одно из тел 1 (рис. 1) помещают на параллельные направляющие 2, образующие с горизонтом углы a1 и a2.
Если тело отпустить, то оно, скатываясь, достигнет нижней точки и, двигаясь далее по инерции, поднимется вверх по направляющим. Движение тела, при котором траектории всех точек лежат в параллельных плоскостях, называется плоским. Плоское движение можно представить двумя способами: либо как совокупность поступательного движения тела со скоростью центра масс и вращательного вокруг оси, проходящей через центр масс; либо как только вращательное движение вокруг мгновенной оси вращения (МОВ), положение которой непрерывно изменяется. В нашем случае эта мгновенная ось Z проходит через точки касания направляющих с движущимся стержнем.
ОПИСАНИЕ МЕТОДА ИЗМЕРЕНИЙ
При скатывании тело, опускаясь с высоты 
, проходит путь l о, а поднимаясь по инерции на высоту 
, проходит путь l. В нижней точке скорость поступательного движения центра масс 
, а угловая скорость тела
, (10)
где t – время движения от верхней точки до нижней, r – радиус стержня (оси).
На скатывающееся тело действует момент сил сопротивления М тр. Работа его на пути l о равна А = М тр j, где угловой путь j0= l 0/ r.
Закон сохранения энергии на отрезке пути l о имеет вид
, (11)
где I – момент инерции скатывающегося тела относительно МОВ,
m – масса тела, включающая в себя массу стержня.
При движении тела вниз с высоты h о и вкатывании его на высоту h работа сил сопротивления на пути (l + l о) равна убыли потенциальной энергии (см. (2)):
. (12)
Решая совместно (10)–(12), получаем формулу для определения момента инерции динамическим методом:
. (13)
Здесь величина (a1+ a2) является константой для данной установки.
Момент инерции тела относительноМОВ определяется теоремой Штейнера
,
где IO – момент инерции, относительно центра масс;
a – расстояние от центра масс тела до оси вращения(в этом опыте a=r).
Задание 1. Аналитический расчёт момента инерции тела
Для расчёта момента инерции маховика I необходимо измерить массу тела (написана на телах) или объём (массу рассчитать, используя плотность) и радиусы цилиндрических тел. Методика расчёта величины I дана в приложении 1. В соответствии с ней результаты всех измерений и вычислений вносите в табл. 1.
Таблица 1
| Индекс | Элементтелавращения | Масса m, кг | Диаметр d, мм, и а, мм | Момент инерции I,кг×м2 | |
| формула | значение | ||||
| Диск | 
| ||||
Далее задание выполняется, как описано в Приложении 1.
Задание 2. Определение момента инерции тела динамическимметодом
1. Определите массу т тела, запишите ее значение, а также постоянную установки (a1+a2) в табл. 2.
2. Проверьте правильность положения установки.При скатывании тело не должно смещаться к одной из направляющих. Для регулировки используйте винты основания. Измерьте штангенциркулем диаметр d стержня в различных местах, определите егоcреднее значение и средний радиус r.
3. Установите тело на направляющие на расстоянии l o от нижней точки, за его положение фиксируется магнитом по нажатию кнопки «Сброс » секундомера.
4. Нажмите кнопку секундомера «Пуск ». При этом электромагнит отключится и тело начинает двигаться. Когда тело достигнет нижней точки, секундомер автоматически выключится. Запишите время движения тела до нижней точки в табл. 2.
5. Наблюдая далее за движением тела по инерции, отметьте расстояние l, на которое оно поднимется до остановки.
6. Опыт повторите еще четыре раза при том же расстоянии l о, записывая результаты в табл. 2.
Таблица 2
| №п.п. | d, мм | t, с | l, м | a1+a2= рад
m = кг
l о = м
 м
|
| … | ||||
| Среднее значение | I = кг×м2 |
7. Найдите средние значения величин r, t, l и по формуле (3.13) рассчитайте момент инерции тела I относительно МОВ.
Задание3. Изучение зависимости момента инерции от распределения массы относительно оси вращения
В этом задании используется тело в виде крестовины, по которой могут перемещаться грузы (цилиндры). Все результаты измерений заносятся в табл. 3.
1. Определите массу т тела и радиус r оси тела, и запишите постоянную установки (a1 + a2).
2. Установите подвижные цилиндры на равном расстоянии b от оси вращения и измерьте это расстояние.
Рис. 2 |  Примечания.
1. Когда грузы находятся на одинаковом расстоянии от оси вращения, тело должно находиться в безразличном положении равновесия на горизонтальных направляющих.
2. Так как цилиндры имеют одинаковый размер, расстояние между центрами грузов равно расстоянию между их торцами,которое можно измерить значительно точнее (рис. 2).
|
Таблица 3
| №п.п. | b | t | b 2 | I | a1 + a2 = рад. т = кг r =мм l 0 = м |
3. Установите тело на направляющие на расстоянии l o от нижней точки, его положение фиксируется магнитом нажатием кнопки «Сброс » секундомера.
4. Нажмите кнопку секундомера «Пуск ». При этом электромагнит отключится и тело начинает двигаться. Когда тело достигнет нижней точки, секундомер автоматически выключится. Запишите время движения тела до нижней точки в табл. 3.
5. Отметьте расстояние l, на которое продвинется тело, поднимаясь по инерции.
6. Повторите измерения пп. 3-5 при других расстояниях b цилиндров, относительно оси вращения.
7. Рассчитайте b 2 и момент инерции тела I (формула 3-13) для каждого опыта.
8. Постройте график зависимости (см. рекомендации построения и обработки графиков) 
и по графику определите момент инерции крестовины IКР и массу m подвижных грузов.
9. Сделайте выводы.
Задание 4. Оценка погрешности измерений
В качестве систематической погрешности в данных опытах следует взять
приборную погрешность, равную цене деления измерительного прибора.
Случайная погрешность определяется по разбросу выборки:
,
где х max и х min– максимальное и минимальное значение измеряемой величины в серии из N повторных измерений. Этой границе доверительного интервала соответствует доверительная вероятность
.
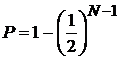1. В табл. 4 занесите средние значения прямых измерений, выполненных в одном из упражнений и значения погрешностей этих величин – систематической и случайной.
2. Для каждой величины выберете наибольшую из погрешностей и рассчитайте наибольшую относительную погрешность δ измерения каждой величины. В окончательном выводе следует отметить для каких величин желательно увеличить (и как?) точность измерений, а для каких её можно и уменьшить без ущерба для конечного результата.
Таблица 4
| ВЕЛИЧИНА | ПОГРЕШНОСТЬ | ||||
| абсолютная | наибольшая | ||||
| название | значение | систематич. | случайная | абсолютная | относит. |
| рад | –– | |||
| т | кг | –– | |||
| м | –– | |||
| l | м | ||||
| r | м | ||||
| t | с |
3. В качестве относительной погрешности результатов измерений примите наибольшую из погрешностей прямых измерений (см. табл. 2)
К о н т р о л ь н ы е в о п р о с ы
1. Укажите величины кинетической и потенциальной энергии при скатывании тела: в начале и в конце движения, в нижней точке и в произвольной точке.
2. Опишите характер движения тела по направляющим. Какая сила создаёт момент относительно оси вращения?
3. Как измеряют угловую скорость w в данной работе?
4. Какие величины измеряют для определения скорости w, момента сил трения, работы сил трения?
5. Какие уравнения лежат в основе динамических методов определения момента инерции?
6. Что составляет основу методики расчётного метода определения величины I?
7. Укажите возможные источники случайных и систематических погрешностей при измерениях.
Приложение 1
МЕТОДИКА РАСЧЕТА МОМЕНТА ИНЕРЦИИ ТЕЛ СЛОЖНОЙ ФОРМЫ
ЦЕЛЬ: приобрести навык расчёта момента инерции тел, состоящих из простых элементов.
1. Исследуйте форму тела. Приняв во внимание, что момент инерции любого тела равен сумме моментов инерции отдельных его элементов, мысленно разделите исследуемое тело на простые элементы, для которых формулы расчёта величины I i даны в табл. 1.
2. Сделайте эскиз исследуемого тела, а если необходимо, то и его элементов, обозначая символами все размеры, подлежащие измерению. Например, тело (рис. 1а) состоит из насаженных на вал 1 шкива 2 и маховика 3 с двумя отверстиями 4. Это тело можно представить (рис. 1б) как совокупность трёх сплошных цилиндров 1, 2 и 3 за вычетом двух малых дисков 4, расположенных на месте отверстий маховика.
 |
Для расчёта момента инерции такого тела
(6)
необходимо знать массы указанных элементов, их радиусы, а также расстояние a от центра отверстий до оси вращения. В случае, если массы m i неизвестны, то для их определения через плотность и объём деталей нужно измерить ещё их длины l 1, l 2 и l 3.
Таблица 1
| № п.п. | Элемент тела вращения | Масса m, кг | Диаметр d, мм, и a, мм | Момент инерции I,кг×м2 | |
| формула | значение | ||||
| Диск |
| ||||
| Вал–шкив | 
| ||||
| Ось | 
| ||||
| 4а) | Кольцо | 
| |||
| б) | Цилиндр |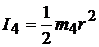 
| |||
| в) | Шар |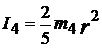 
| |||
| г) | Стержень | 
| |||
| д) | Пластина | (b x d) | 
| ||
| Тело | 
| a = | 
| ||
|
Примечания:
а) значения I i и I с даны относительно оси, проходящей через центр масс;
б) для стержня длиной l и пластины размером b´d значения I даны относительно оси, перпендикулярной их плоскости;
в) в формуле для I с: n – число одинаковых элементов; знак «минус» для случая, если отверстия в диске имеют форму четвертого элемента.
3. Получите формулу вида (3.6) для расчёта момента инерции тела относительно оси, проходящей через центр масс системы.
4. Запишите в табл. 1 массы m i отдельных частей тела, а если они неизвестны, то плотность вещества r.
5. Измерьте линейкой или штангенциркулем (в отчёте объясните выбор инструмента) величины, необходимые для расчёта момента инерции каждого элемента тела. Результаты измерений записывайте в табл. 1.
6. Вычислите моменты инерции отдельных элементов, а затем момент инерции тела I с относительно оси, проходящей через центр масс.
7. Рассчитайте, если это необходимо в данной работе, момент инерции тела относительно МОВ, используя теорему Штейнера (3.5).
8. Оцените систематическую (приборную) погрешность прямых измерений (с. 7), сделанных для расчёта величины I. Результаты внесите в табл. 2.
Таблица 2
| Измеряемый параметр | Величина | Систематическая погрешность DS | Относительная погрешность d |
| d i | 
|
9. В выводе оцените соотношение величин I i частей тела. Какие из них пренебрежимо малы и по какой причине? По данным табл. 2 сделайте вывод о том, какие измерения проведены с достаточной точностью, а какие – нет; связано ли последнее с используемым инструментом?