Разбиение спецификации программы

 

Задача доопределения. Пусть решена задача второго этапа и выполнено расширение подмножеств 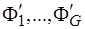до подмножеств 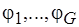, причем 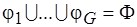(см. п. 5.1). Дело в том, что процедура отыскания общего описания 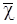архитектуры для 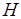семейств признаков, основанная на поиске максимального нуль-единичного потока в сети 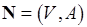, вовсе не гарантирует получения разбиения спецификации 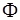согласно найденному описанию. Теперь, на третьем этапе необходимо найти разбиение 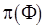, соответствующее описанию 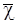. Это разбиение назовем доопределением семейства 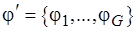расширенных подмножеств. Можно проиллюстрировать необходимость доопределения с помощью диаграмм, приведенных на рис. 5.14. На рис. 5.14, а показаны пересекающиеся множества семейства 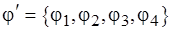. Эти множества соответствуют расширенным подмножествам 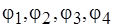объектов спецификации и четырем функциям целевой архитектуры. На рис. 5.14, б показан один из возможных вариантов доопределения, результатом которого является разбиение множества 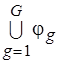, где 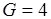, на четыре блока.

При этом , , , , , .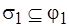

 

 

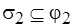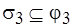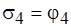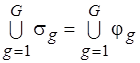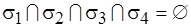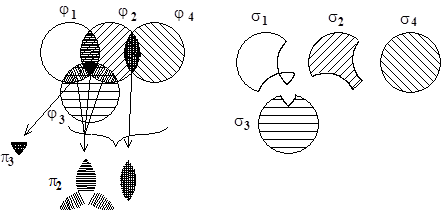
а) б)

 

Рис. 5.14. Иллюстрация процедуры доопределения

 

Обозначим через 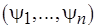последовательность различных элементов пересечений множеств 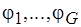, а через 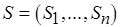– семейство непустых непересекающихся множеств. При этом имеют место биекции 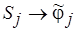, где 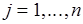, 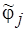– совокупность пересекающихся множеств семейства 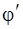таких, что 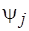– элемент пересечения, а 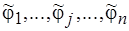не обязательно не пересекаются.

Рассмотрим 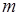-элементное множество 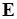, для которого 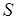является разбиением и 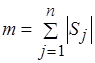. Упорядочим элементы 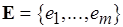по невозрастанию неотрицательных вещественных весов: .

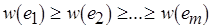Задача оптимального доопределения заключается в том, чтобы найти подмножество 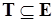с наибольшим весом 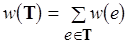, где 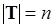. Это означает, что необходимо отобрать 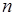подмножеств 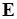, пересечения которых образуют последовательность 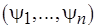. В результате доопределения каждый элемент 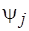должен быть закреплен за одним и только одним из пересекающихся подмножеств 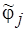и исключен из других (см. рис. 5.14, б). При этом сумма весов подмножеств, за которыми закрепляются элементы 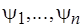, должна быть наибольшей.

Основные этапы доопределения. Для оптимального доопределения разбиения необходимо, во-первых, выделить последовательность 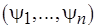, все элементы которой различны; во-вторых, построить семейство 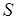; в-третьих, из множеств 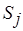семейства 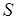отобрать 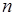разных элементов, сумма весов которых будет наибольшей.

На первом этапе доопределения выполним следующие операции. Найдем пересечение 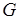множеств семейства : , .

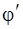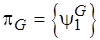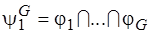Далее найдем все пересечения 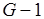множеств из 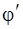, число которых не превышает числа сочетаний 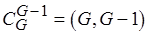: 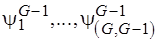. Построим разбиение вида .

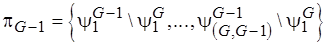Рекуррентно продолжим построение разбиений, отыскивая на шаге 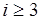все пересечения 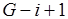множеств 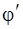. Их не более 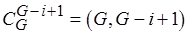, т.е. 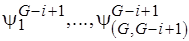. Рассмотрим некоторое пересечени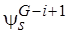е , где 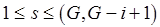. Пусть 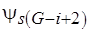– объединение всех пересечений множеств 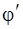, найденных на 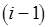-м шаге и участвующих в образовании пересечения 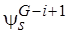на шаге 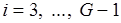. Построим следующее разбиение:

.

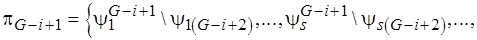
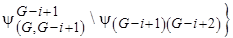Поскольку индекс 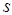изменяется от 1 до 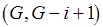, а число пересечений на 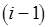-м шаге не превышает 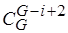, то некоторые подмножества 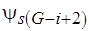являются пустыми.

Наконец, найдем попарные пересечения 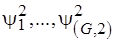, где 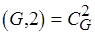и построим разбиение вида

,

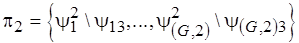где 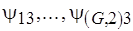– объединения блоков разбиения пересечений из 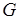по 3 тех подмножеств, которые участвуют в формировании попарных пересечений .

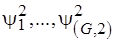Результатом первого этапа является семейство разбиений 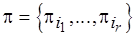множества пересечений элементов семейства 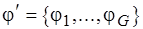, где , .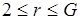

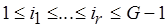Проиллюстрируем первый этап диаграммами рис. 5.14, а. На шаге 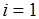отыскивается разбиение 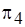: оно пусто. На шаге 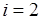получаем разбиение 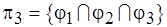, 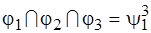. На шаге 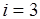строится разбиение попарных пересечений, причем из его блоков удаляются элементы, вошедшие в пересечение при :

.

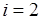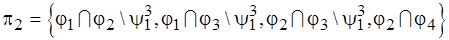Таким образом, получается семейство 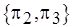разбиений пересечений множеств .

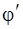На втором этапе пронумеруем элементы 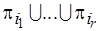, определив последовательность 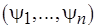, где 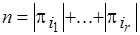. После первого этапа известны пересекающиеся множества, образующие 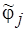, элементом которых является 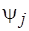, 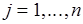. Сопоставим каждому элементу 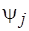множество 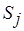, элементы которого находятся во взаимно однозначном соответствии с элементами множества 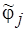. Если при этом одним и тем же пересекающимся множествам из 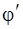, содержащим 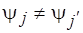, , 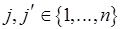соответствуют различные элементы 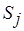, , 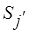причем 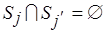, то получаем разбиение .

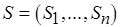На третьем этапе необходимо решить, какому элементу множества 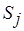соответствует элемент 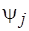. Тогда в итоге объект спецификации 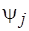будет закреплен за одним и только одним из множеств совокупности .

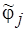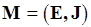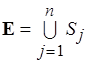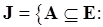
Обоснование процедуры оптимального доопределения. Рассмотрим матроид разбиений , где , 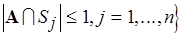. Тогда для того, чтобы найти какое-либо решение задачи доопределения, нужно отыскать одну из баз этого матроида (см. п. 5.4).

 

Пусть 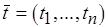– трансверсаль семейства 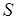, независимая относительно матроида 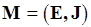(см. п. 5.4). Тогда 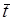является одним из решений задачи доопределения. Действительно, прежде всего, на основании теоремы Радо можно утверждать, что такая трансверсаль всегда существует, поскольку объединение любых 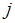подмножеств 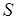, имеет ранг, не меньший чем 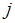(см. п. 5.4). Это следует из способа построения семейства 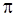, последовательности 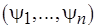и семейства .

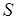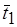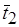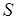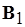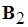Пусть и – две различные трансверсали . Объединения их элементов и , соответственно, удовлетворяют аксиомам баз, поскольку 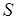– разбиение :

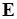1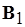) ни , ни 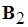не включают друг друга;

2) 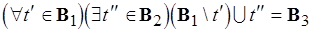– база, поскольку 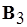– максимальное независимое множеств ранга 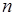матроида 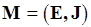. Следовательно, 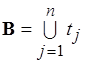– одна из баз матроида 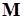. Между множеством трансверсалей семейства 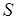и множеством баз матроида 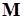существует взаимно однозначное соответствие.

Построим доопределение по шагам, ассоциируя 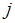-й шаг с анализом множества 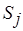. Пусть элемент 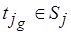трансверсали 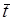соответствует множеству 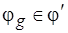, , 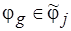, 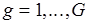элементом которого является 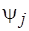. Тогда оставляем без изменения множество 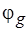и исключаем элемент 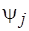из остальных 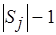подмножеств совокупности 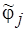. Получаем новое семейство 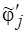и переходим к 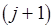-му шагу. Число таких шагов равно 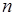. После получения семейства 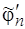задача доопределения решена, поскольку в результате построено семейство, являющееся разбиением 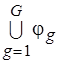. На каждом из шагов доопределения элементы пересечения множеств из 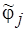оставались в одном и только одном из множеств 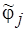и исключались из других.

Вышерассмотренная процедура дает возможность нахождения какого-либо из доопределений, число которых может быть и более одного, поскольку на каждом из 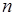этапов произвольно выбирается подмножество 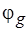, остающееся без изменения. В примере на рис. 5.14, б разбиение 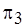закрепляется за множеством 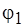, а "лепестки" разбиения 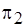распределены между множествами 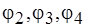. Сложность нахождения какого-либо решения 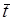задачи доопределения составляет 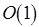, т.е. не зависит от 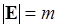. Действительно, для любого доопределения элемент 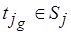можно выбирать совершенно произвольно и, соответственно, элемент 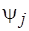можно закрепить за любым из множеств .

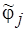Практически важнее другой случай, когда отыскивается оптимальное решение 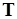задачи доопределения спецификации программы.

Т е о р е м а 5.3. Сложность нахождения оптимального по Гейлу решения задачи доопределения составляет .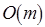

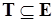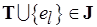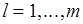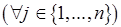
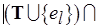
Д о к а з а т е л ь с т в о. Применяя жадный алгоритм (см. п. 5.4), можно сформировать подмножество , являющееся базой с наибольшим весом. При этом проверка условия включения в базу , где , осуществляется на основании следующей посылки: 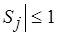. Тем самым мы находим множество 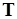, оптимальное в очень сильном смысле – по Гейлу (см. п. 5.4): в любом независимом множестве вес 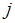-го по величине элемента не больше веса 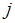-го по величине элемента в .

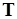Число шагов жадного алгоритма имеет порядок 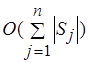, поскольку 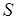является разбиением 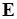. Для каждого из 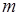элементов 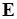нужно лишь проверить условие его включения в базу 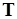с наибольшим весом. Теорема доказана.

Линейная оценка сложности поиска оптимального по Гейлу решения задачи доопределения – следствие специальной организации семейств 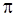и 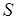. Заметим, что наибольшее значение 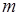равно 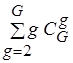. Действительно, число членов семейства 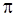не превышает .

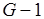При этом 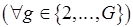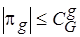, а мощность множеств из 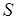, соответствующих 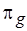, равна .

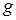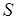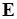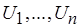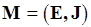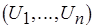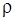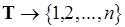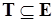Положим, что не является разбиением , т. е. содержит не обязательно непересекающиеся множества , а – матроид трансверсалей (см. п. 5.4). Тогда поиск оптимального по Гейлу решения задачи доопределения включает в себя отыскание наибольшей по весу трансверсали семейства и биекции : , где и 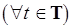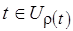. Сложность нахождения наибольшей по весу трансверсали и биекции 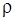имеет порядок 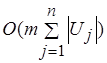. Поскольку 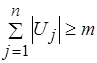, то это означает не менее чем квадратичную оценку сложности, что подчеркивает преимущество рассмотренной процедуры доопределения с линейной временной асимптотической сложностью.

Заметим, что поиск разбиения конечного множества элементов произвольной природы на блоки, удовлетворяющие заданным требованиям, является весьма распространенной оптимизационной задачей. Часто эту задачу удается свести к задаче доопределения до разбиения некоторого "промежуточного" представления исходного множества (об этом уже говорилось в конце п. 5.1, где речь шла о разбиении спецификации вычисления 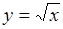). В этом подразделе мы рассмотрели процедуру доопределения, результатом которой является разбиение спецификации программы на блоки, оптимальные в очень сильном смысле – по Гейлу. Сложность поиска оптимального по Гейлу решения задачи доопределения линейно зависит от суммарного числа пересечений множеств "промежуточного" представления.

В заключение данного подраздела подведем некоторые итоги.

Синтез описания целевой архитектуры и построение соответствующей ему начальной фрагментации спецификации – взаимосвязанные процедуры (см. п. 5.1).

Целевая архитектура определяет способ функционирования системы посредством разрешенного набора 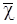признаков и разбиения 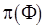спецификации программы в соответствии с функциями, реализуемыми вычислительной системой для выполнения программы.

Разобранный подход к синтезу архитектуры включает в себя поиск ее частичного описания (см. п. 5.2) с последующим построением полного набора архитектурных признаков; отыскание общего описания для разных вариантов начальной фрагментации (см. п. 5.2), далее, построение разбиения спецификации, соответствующего найденному описанию (см. п. 5.3).

Наконец, необходимо подчеркнуть, что вышерассмотренные комбинаторные схемы и методы ни в коей мере не претендуют на полную формализацию процесса синтеза архитектуры. Они изначально основываются на экспертных знаниях и предназначены для того, чтобы "справиться" с объективно существующей неполнотой этих знаний о реализации функций, заданных спецификацией программы, и неизбежно высокой трудоемкостью обоснованного выбора архитектурного решения.

 

 

Комментарий к разделу 5

 

Краткая сводка необходимых сведений по комбинаторике и теории графов. Основной математический аппарат, который используется в этой главе, это – потоки в сетях и связанные с ними задачи, а также теория матроидов и жадные алгоритмы. Именно по этим разделам теории графов и комбинаторики ниже приводится минимум сведений, которые нужны для понимания отдельных этапов синтеза целевой архитектуры.

Существует целый ряд алгоритмов поиска на графах, использующих систематический просмотр вершин, когда каждая из них анализируется лишь однажды. Один из методов, использующихся в таких алгоритмах, называется поиском в ширину. Его основная идея заключается в следующем. Выбирается произвольная вершин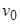а графа 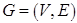с множеством 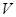вершин и множеством 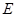дуг. Определяются все вершины-соседи, т.е. вершины, находящиеся от 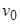на расстоянии в одну дугу. Произвольно выбирается вершина 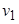из окружения вершины 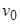и рассматривается окружение 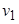. Процесс продолжается до тех пор, все вершины графа 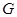не будут просмотрены.

При поиске в глубину просмотр также начинается с некоторой произвольной вершины 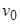. Затем просматривается какая-либо вершина 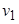, смежная с 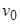, и процесс повторяется от вершины 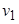. Если не существует вершин смежных с 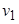, то осуществляется возврат к 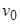и выбирается другая, смежная с ней вершина. Таким образом, в отличие от поиска в ширину, поиск в глубину от вершины 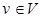основан на просмотре всех вершин, смежных с .

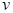Для определения трудоемкости, или сложности, алгоритма часто используют 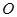-символику. Говорят, что неотрицательная функция 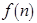, где 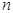– размерность входа (натуральное число), не превосходит по порядку функцию 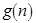, если существуют такие константы 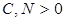, что 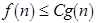для всех 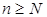. При этом используется запись 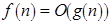. Запись 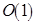означает, что сложность алгоритма не зависит от размерности входа. В такой символике временная сложность (число шагов) многих алгоритмов, использующих методы поиска в ширину или глубину, составляет .

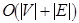Сетью обычно называют произвольный ориентированный граф 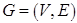, каждой дуге которого некоторая функция (поток) ставит в соответствие неотрицательное вещественное число, называемое пропускной способностью дуги. В сети выделяются две вершины – источник 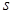и сток 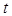. Величину, равную сумме весов дуг, исходящих из источника 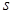или входящих в сток 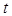, называют величиной потока. Поток не возникает и не накапливается ни в одной из вершин 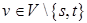. Алгоритмы построения потока с максимальной величиной (максимального потока), как правило, основываются на последовательном увеличении потока.

Произвольное подмножество 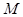попарно несмежных ребер неориентированного графа называется паросочетанием. Паросочетание является наибольшим, если число ребер в нем наибольшее среди всех паросочетаний графа. В двудольном графе 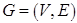множество вершин 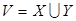можно разбить на непересекающиеся подмножества 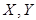, а каждое ребро 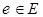имеет вид 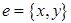, где 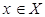, 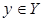. Задачу нахождения наибольшего паросочетания в таком графе 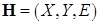можно свести к поиску максимального потока в сети 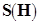, построенной на этом графе (см. п. 5.2). Существует взаимно однозначное соответствие между нуль-единичными потоками в 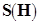и паросочетаниями в двудольном графе 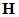. При этом величина потока равна мощности соответствующего паросочетания. Для данного паросочетания 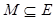чередующейся цепью относительно 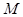называется произвольное подмножество дуг 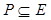, которое однозначно определяется последовательностью различных вершин 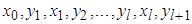, , 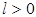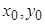– свободные вершины в 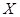, 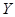соответственно. При этом .

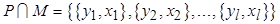Метод Хопкрофта – Карпа позволяет найти наибольшее паросочетание в двудольном графе 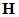с 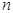вершинами за 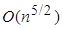шагов. Идея метода состоит в следующем. Для заданного двудольного графа 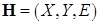строится вспомогательная бесконтурная сеть, пропускные способности всех дуг которой равны единице. Затем специальная процедура находит максимальное множество непересекающихся кратчайших чередующихся цепей. Эта процедура ведет поиск в глубину во вспомогательной бесконтурной сети, начиная с источника 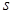. При этом существующее паросочетание увеличивается вдоль максимального множества путей из 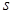в 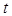с попарно различными подмножествами вершин во вспомогательной сети. Число фаз, увеличивающих паросочетание, имеет порядок 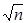. Поскольку сложность построения вспомогательной сети определяется порядком числа шагов поиска в глубину, то сложность алгоритмов, реализующих метод Хопкрофта – Карпа, имеет порядок 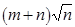, где 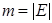. Ясно, что 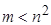. Отсюда и получается сложность .

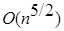С помощью метода Хопкрофта – Карпа для заданного семейства 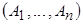можно найти систему различных представителей (трансверсаль) или установить, что ее не существует за время порядка .

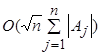Необходимое и достаточное условие существования трансверсали было получено Ф. Холлом.

Т е о р е м а Х о л л а. Трансверсаль семейства 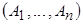существует тогда и только тогда, когда , .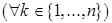

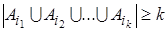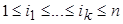С паросочетаниями в двудольном графе 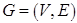связано и отыскание вершинного покрытия, которое представляет собой произвольное подмножество 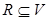такое, что любое ребро из 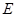инцидентно некоторой вершине из 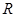. В произвольном двудольном графе максимальная мощность паросочетания равна минимальной мощности вершинного покрытия. Нужно заметить, что 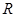является вершинным покрытием тогда и только тогда, когда в множестве 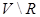никакие две вершины не являются смежными ( 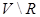называют независимым множеством вершин).

Рассмотрим следующую задачу. Пусть 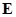– непустое конечное множество, 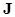– семейство его подмножеств, т.е. 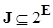, 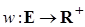– функция, значениями которой являются неотрицательные вещественные числа из 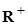. Она каждому элементу 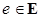присваивает некоторый неотрицательный вес 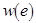. Необходимо из 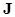выбрать подмножество 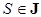с наибольшей суммой весов его элементов .

 

 

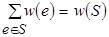В некоторых случаях эту оптимизационную задачу можно решить с помощью так называемого жадного алгоритма:

1°. Упорядочить множество 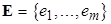по невозрастанию весов: .

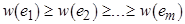2°. .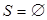

3°. Если 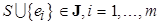, то 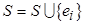, иначе останов.

Возникает вопрос, всегда ли жадный алгоритм правильно находит подмножество 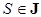с наибольшим весом? Оказывается так происходит тогда, когда пара 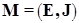является матроидом.

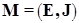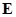Матроид – произвольная пара , где – конечное непустое множество, а 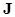– семейство его подмножеств, удовлетворяющих двум следующим аксиомам независимости.

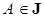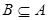I1. Если и , то ().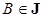

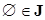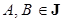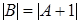I2. Если и , то .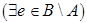

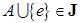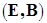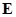Иногда матроид определяется как пара , где – конечное непустое множество, а 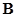– семейство его подмножеств (баз), удовлетворяющих аксиомам баз.

B1. Никакая база не содержится в другой базе.

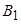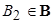B2. Если и , то .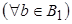

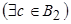
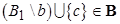Базы являются независимыми равномощными множествами. Мощность базы называется рангом матроида.

Т е о р е м а Р а д о – Э д м о н д с а. Если 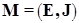матроид, то множество 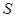, найденное жадным алгоритмом является независимым множеством с наибольшим весом. Если 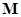не является матроидом, то найдется функция 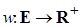, такая что 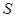не будет независимым множеством с наибольшим весом.

Множество 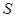, найденное жадным алгоритмом является оптимальным в сильном смысле – по Гейлу: в любом другом независимом множестве 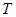вес 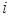-го по величине элемента не больше веса 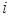-го по величине элемента в 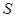. Таким образом, жадный алгоритм отбирает такое множество 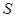, в котором 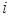-й по величине элемент не меньше 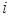-го по величине элемента произвольной базы.

В п. 5.2 упоминается следующая

Т е о р е м а Э д м о н д с а и Ф а л к е р с о н а. Пусть 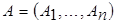– семейство подмножеств конечного множества 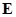, 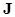– семейство частичных трансверсалей 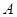. Тогда 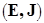является матроидом.

Семейство 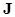удовлетворяет аксиомам независимости I1 и I2 (при этом иногда соответствующим образом изменяется формулировка теоремы Эдмондса – Фалкерсона).

Такой матроид называется матроидом трансверсалей семейства .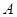

Часто нужно отыскивать трансверсаль семейства 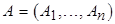, которая является независимой относительно матроида 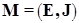( 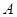– семейство подмножеств множества 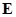). Эта трансверсаль является независимым подмножеством матроида. Теорема Радо, частным случаем которой является теорема Холла, отвечает на вопрос о существовании такой трансверсали.

Т е о р е м а Р а д о. Пусть 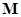– матроид с множеством элементов 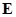, 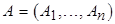– семейство непустых подмножеств множества 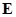. Трансверсаль семейства 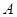, независимая относительно матроида 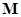, существует тогда и только тогда, когда для 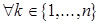объединение любых 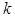подмножеств 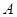имеет ранг не меньший .

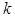Пусть 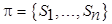– произвольное разбиение множества 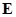, семейство подмножеств которого определяется так:

.

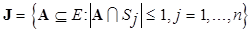Пару 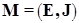в этом случае называют матроидом разбиений.