НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ
БЕЗУСЛОВНОГО ЭКСТРЕМУМА
Задача
Дана дважды непрерывно дифференцируемая функция  , определённая на множестве
, определённая на множестве  .
.
Требуется определить точки  её локальных минимумов и максимумов на
её локальных минимумов и максимумов на 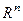 .
.
Последовательность решения
Вначале с помощью необходимых условий первого и второго порядка (порядок условий определяется порядком используемых производных) необходимо найти точки  , где могут быть локальные экстремумы. Затем в найденных точках проверяется выполнение достаточных условий безусловного экстремума. В точках экстремума вычисляются значения исследуемой функции
, где могут быть локальные экстремумы. Затем в найденных точках проверяется выполнение достаточных условий безусловного экстремума. В точках экстремума вычисляются значения исследуемой функции  .
.
1.1.Необходимые условия экстремума первого порядка
Пусть  есть точка локального минимума (максимума) функции
есть точка локального минимума (максимума) функции  на множестве
на множестве 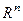 и
и  дифференцируема в точке
дифференцируема в точке  . Тогда градиент функции
. Тогда градиент функции  в точке
в точке  равен нулю, т.е.
равен нулю, т.е.
 или
или  (1)
(1)
Точки, удовлетворяющие условию (1), называются с тационарными.
1.2. Необходимые условия экстремума второго порядка
Пусть 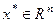 есть точка локального минимума (максимума) функции
есть точка локального минимума (максимума) функции  на множестве
на множестве  и
и  дважды дифференцируема в точке
дважды дифференцируема в точке  . Тогда матрица Гессе
. Тогда матрица Гессе  функции
функции  , вычисленная в точке
, вычисленная в точке  , является положительно (отрицательно) полуопределённой, т.е.
, является положительно (отрицательно) полуопределённой, т.е.
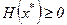 , (
, ( ) (2)
) (2)
1.3. Достаточные условия экстремума
Функция  в точке
в точке  дважды дифференцируема, её градиент равен нулю (необходимое условие экстремума первого порядка), а матрица Гессе является положительно (отрицательно) определённой:
дважды дифференцируема, её градиент равен нулю (необходимое условие экстремума первого порядка), а матрица Гессе является положительно (отрицательно) определённой:
 ,
,  , (
, (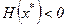 ). (3)
). (3)
Тогда точка  есть точка локального минимума (максимума) функции
есть точка локального минимума (максимума) функции  на множестве
на множестве 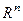 .
.
Определение 1
Рассмотрим определитель матрицы Гессе  , вычисленный в стационарной точке
, вычисленный в стационарной точке
 . (4)
. (4)
Определители
 ,
,  ,…,
,…, 
называются угловыми минорами матрицы Гессе.
Определители m –го порядка ( ), получающиеся из определителя матрицы
), получающиеся из определителя матрицы  вычёркиванием каких-либо
вычёркиванием каких-либо  строк и
строк и  столбцов с одними и теми же номерами, называются главными минорами.
столбцов с одними и теми же номерами, называются главными минорами.
Проверка достаточных условий экстремума
Достаточные условия экстремума и необходимые условия 2-го порядка могут быть проверены двумя способами.
1-й способ основан на исследовании угловых миноров.
Для того, чтобы матрица Гессе  была положительно определённой (
была положительно определённой ( ) необходимо и достаточно, чтобы все угловые миноры этой матрицы были положительны:
) необходимо и достаточно, чтобы все угловые миноры этой матрицы были положительны:
 ,
,  , …,
, …, 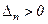 (5)
(5)
Для того чтобы матрица Гессе  была отрицательно определённой (
была отрицательно определённой (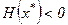 ) необходимо и достаточно, чтобы знаки угловых миноров этой матрицы чередовались, начиная с минуса:
) необходимо и достаточно, чтобы знаки угловых миноров этой матрицы чередовались, начиная с минуса:
 ,
,  ,
,  ,…,
,…,  (6)
(6)
Для того, чтобы матрица Гессе  была положительно полуопределённой (
была положительно полуопределённой (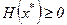 ) необходимо и достаточно, чтобы все главные миноры этой матрицы были неотрицательны.
) необходимо и достаточно, чтобы все главные миноры этой матрицы были неотрицательны.
Для того, чтобы матрица Гессе  была отрицательно полуопределённой (
была отрицательно полуопределённой ( ) необходимо и достаточно, чтобы все главные миноры чётного порядка этой матрицы были неотрицательны, а все главные миноры нечётного порядка – неположительны.
) необходимо и достаточно, чтобы все главные миноры чётного порядка этой матрицы были неотрицательны, а все главные миноры нечётного порядка – неположительны.
Определение 2
Составим уравнение
 . (7)
. (7)
Это алгебраическое уравнение называется характеристическим уравнением матрицы  . Корни этого уравнения называются собственными числами матрицы
. Корни этого уравнения называются собственными числами матрицы  .
.
2-й способ основан на проверке собственных чиселматрицы Гессе
Для того, чтобы матрица Гессе  была положительно определённой (
была положительно определённой ( ) необходимо и достаточно, чтобы все собственные числа этой матрицы были положительны:
) необходимо и достаточно, чтобы все собственные числа этой матрицы были положительны:
 ,
,  , …,
, …,  (8)
(8)
Для того чтобы матрица Гессе  была отрицательно определённой (
была отрицательно определённой (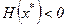 ) необходимо и достаточно, чтобы все собственные числа этой матрицы были отрицательны
) необходимо и достаточно, чтобы все собственные числа этой матрицы были отрицательны
 ,
,  , …,
, …,  (9)
(9)
Для того, чтобы матрица Гессе  была положительно полуопределённой (
была положительно полуопределённой (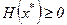 ) необходимо и достаточно, чтобы все собственные числа этой матрицы были неотрицательны.
) необходимо и достаточно, чтобы все собственные числа этой матрицы были неотрицательны.
Для того, чтобы матрица Гессе  была отрицательно полуопределённой (
была отрицательно полуопределённой ( ) необходимо и достаточно, чтобы все собственные числа этой матрицы были неположительны.
) необходимо и достаточно, чтобы все собственные числа этой матрицы были неположительны.
Алгоритм решения задачи нахождения безусловного экстремума функции отображён на рис.1. На рисунке ромб – означает проверку условия, описанного в этой фигуре, прямоугольник со скруглёнными углами– окончание исследования. В табл.1 приведены все способы проверки условий экстремума.
Пример 1. Найти экстремум функции  на множестве
на множестве  .
.
Запишем необходимые условия экстремума первого порядка:
 ;
; 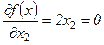 (10)
(10)
В результате решения системы уравнений (10) Получим одну стационарную точку  .
.
Проверим выполнение достаточных условий экстремума:
1-й способ. Матрица Гессе имеет вид  . При этом
. При этом  ,
, 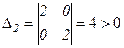 . Следовательно, в точке
. Следовательно, в точке  локальный минимум.
локальный минимум.
2-й способ. Найдём собственные числа матрицы Гессе. Для этого решим уравнение
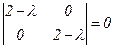 . Отсюда
. Отсюда  и
и  . Все собственные числа положительны, следовательно, в исследуемой точке функция имеет локальный минимум. Результаты исследования обоими способами совпадают.
. Все собственные числа положительны, следовательно, в исследуемой точке функция имеет локальный минимум. Результаты исследования обоими способами совпадают.
Вычислим значение функции в точке минимума:
 .
.
Пример 2. Найти экстремум функции  на множестве
на множестве  .
.
Запишем необходимые условия экстремума первого порядка:
 ;
; 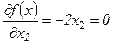 (11)
(11)
В результате решения системы уравнений (11) получим одну стационарную точку  .
.
Проверим выполнение достаточных условий экстремума.
1-й способ. Матрица Гессе имеет вид  .
.

 ,
,  ,
,
следовательно, достаточные условия экстремума не выполняются.
Проверяем необходимые условия экстремума второго порядка. Главные миноры первого ( )порядка получаются из
)порядка получаются из  в результате вычёркивания
в результате вычёркивания 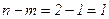 строк и столбцов с одинаковыми номерами и равны
строк и столбцов с одинаковыми номерами и равны  и 2. Главный минор второго порядка (
и 2. Главный минор второго порядка ( ) получается из
) получается из  в результате вычёркивания
в результате вычёркивания  строк и столбцов, т.е совпадает с
строк и столбцов, т.е совпадает с  . Отсюда следует, что необходимые условия второго порядка не выполняются. Т.к. матрица Гессе не является нулевой, то можно сделать вывод, что в точке
. Отсюда следует, что необходимые условия второго порядка не выполняются. Т.к. матрица Гессе не является нулевой, то можно сделать вывод, что в точке  нет экстремума.
нет экстремума.
2-й способ. Найдём собственные значения матрицы Гессе в соответствии с (7) из уравнения
 .
.
Получим 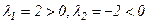 , т.е. собственные значения имеют разные знаки. Поэтому точка
, т.е. собственные значения имеют разные знаки. Поэтому точка  не является точкой минимума или максимума.
не является точкой минимума или максимума.
Функция  не имеет экстремумов.
не имеет экстремумов.
Пример 3. Найти экстремум функции  на множестве
на множестве  .
.
Запишем необходимые условия экстремума первого порядка:
 ;
; 
В результате решения системы получаем стационарную точку 
Матрица Гессе имеет вид  .
.  ,
,  следовательно, достаточные условия экстремума не выполняются.
следовательно, достаточные условия экстремума не выполняются.
Проверяем необходимые условия экстремума второго порядка. Главные миноры первого порядка равны 2 и 0 соответственно. Главный минор второго порядка – 0. Т.к. все главные миноры неотрицательны, то в точке  может быть минимум и требуется дополнительное исследование.
может быть минимум и требуется дополнительное исследование.
Вычислим значение функции в точке  :
:  и рассмотрим поведение функции
и рассмотрим поведение функции  на множестве
на множестве  . При любых
. При любых 
 , поэтому точка
, поэтому точка  является точкой глобального минимума.
является точкой глобального минимума.
Пример 4. Найти экстремум функции  на множестве
на множестве  .
.
Запишем необходимые условия экстремума первого порядка:
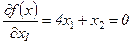 ;
;  .
.
В результате решения системы получаем стационарную точку 
Проверим выполнение достаточных условий экстремума первым способом. Матрица Гессе имеет вид
 .
.  ,
,
следовательно, точка  является точкой локального минимума. Поскольку
является точкой локального минимума. Поскольку  , то в точке
, то в точке  функция строго выпуклая, поэтому точка
функция строго выпуклая, поэтому точка  - точка глобального минимума. Вычислим значение функции в точке
- точка глобального минимума. Вычислим значение функции в точке  :
:  .
.
Пример 5. Найти экстремум функции  на множестве
на множестве  .
.
Запишем необходимые условия экстремума первого порядка: 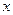
 ;
;  .
.
В результате решения системы получаем стационарную точку 
Проверим выполнение достаточных условий экстремума первым способом. Матрица Гессе имеет вид  . Т.к.
. Т.к.  ,
,  , то в точке
, то в точке  локальный минимум. Поскольку
локальный минимум. Поскольку  , то в точке
, то в точке  функция строго выпуклая, поэтому точка
функция строго выпуклая, поэтому точка  - точка глобального минимума. Вычислим значение функции в точке
- точка глобального минимума. Вычислим значение функции в точке  :
:  .
.
Пример 6. Найти экстремум функции 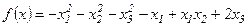 на множестве
на множестве  .
.
Запишем необходимые условия экстремума первого порядка: 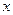
 ,
,  ,
,  .
.
В результате решения системы получаем стационарную точку 
Проверим выполнение достаточных условий экстремума.
1-й способ. Матрица Гессе имеетвид
 .
.
Т.к.  ,
,
т.е знаки угловых миноров чередуются, начиная с минуса, то точка  - точка локального максимума.
- точка локального максимума.
2-й способ. Найдём собственные значения матрицы Гессе в соответствии с (7) из уравнения:
 .
.
Отсюда
 и
и
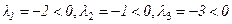 .
.
Т.к. все собственные числа матрицы Гессе отрицательны, то в точке  локальный максимум. Вычислим значение функции в точке
локальный максимум. Вычислим значение функции в точке  :
:  .
.
Задачи для самостоятельного решения
1. Найти безусловный экстремум функции
 .
.
2. Проверить, является ли точка  точкой безусловного экстремума функции
точкой безусловного экстремума функции  .
.
3. Найти безусловный экстремум функции 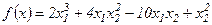 .
.
4. Найти безусловный экстремум функции  .
.
5. Найти безусловный экстремум функции 
6. Найти безусловный экстремум функции  .
.
7. Проверить, является ли точка  точкой безусловного минимума функции
точкой безусловного минимума функции  .
.
8. Найти безусловный экстремум функции  .
.
9. Проверить, являются ли точки  точками безусловного минимума функции
точками безусловного минимума функции  .
.
10. Проверить, являются ли точки  точками экстремума функции
точками экстремума функции  .
.