Чертежи разверток поверхностей геометрических тел
Цель: Научить выполнять проецирование предмета на 3 плоскости.
Развивать пространственное мышление.
Воспитывать аккуратность при выполнении чертежей.
Методы: Беседа, объяснение, демонстрация, самостоятельная работа.
Оборудование: Учебник, плакат, чертежные инструменты, модели.
Тип урока: Изучение нового материала
Структура урока
1. Орг. момент – 2-3 мин.
2. Новый материал – 15 мин.
3. Практическя работа - 25 мин.
4. Подведение итогов – 3 мин.
Ход урока
Орг. момент.
Здравствуйте, садитесь.
Тема сегодняшнего урока – «Чертежи разверток поверхностей геометрических тел ». Запишите её в тетрадь чертёжным шрифтом (тема написана на доске).
Новый материал
Для изготовления ограждений станков, вентиляционных труб и некоторых других изделий вырезают из листового материала их развертки.
Развертка поверхностей любой прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух оснований — многоугольников.
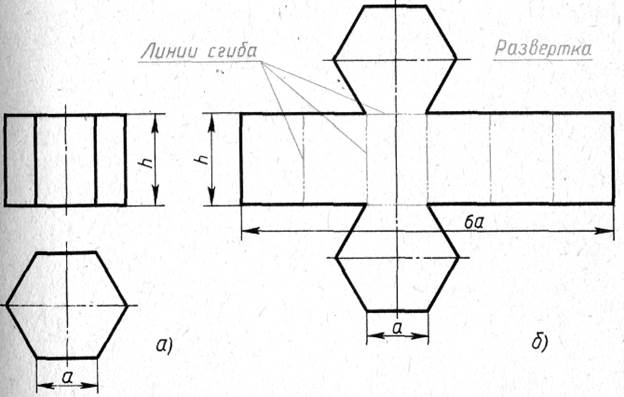
Рис 139.
.
Чертежи разверток поверхностей конуса и пирамиды, шестиугольной призмы цилиндра.
Например, у развертки поверхностей шестиугольной призмы (рис. 139, б) все грани — равные между собой прямоугольники шириной а и высотой, a основания — правильные шестиугольники со стороной, равной а.
Таким образом, можно построить чертеж развертки поверхностей любой призмы.
Развертка поверхностей цилиндра состоит из прямоугольника и двух кругов (рис. 140, б). Одна сторона прямоугольника равна высоте цилиндра, другая — длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра
Развертка поверхностей конуса представляет собой плоскую фигуру, состоящую из сектора — развертки боковой поверхности и круга — основания конуса (рис. 141, б).
Построения выполняются так:
1. Проводят осевую линию и из точки s' на ней описывают радиусом, равным длине s'a' образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса.
Точку s соединяют с концевыми точками дуги.
Рис 140.
2. К полученной фигуре — сектору
пристраивают круг. Диаметр этого круга равен диаметру основания конуса.
Длину окружности при построении сектора можно определить
по формуле С = nD.
Угол а подсчитывают по формуле 
,
Где:
d — диаметр окружности основания,
R — длина образующей конуса, ее можно подсчитать по теореме Пифагора.
Чертеж развертки поверхностей пирамиды строят так(рис. 142, б).
Из произвольной точки О описывают дугу радиуса R, равного длине бокового ребра пирамиды. На этой дуге откладывают четыре отрезка, равные стороне основания. Крайние точки соединяют прямыми с точкой О. Затем пристраивают квадрат, равный основанию пирамиды.
Обратите внимание, как оформляют чертежи разверток. Над изображением пишут «Развертка» с чертой внизу. От линий сгиба, которые проводят штрихпунктирной с двумя точками, проводят линии-выноски и пишут на полке «Линии сгиба».
Рис 142.
Построение разверток выполняется обычно графическими приемами, с применением способов, предлагаемых начертательной геометрией.
Поверхности деталей, ограниченных плоскостями или развертывающимися кривыми поверхностями, могут быть развернуты и совмещены с плоскостью точно.
В этом случае на развертке сохраняются точки (отрезки), лежащие на поверхности, причем каждой точке (отрезку прямой) на развертке соответствует вполне определенная и единственная точка (отрезок прямой) на поверхности детали, и наоборот.
На рисунке изображены развертки поверхностей многогранных тел и тел вращения.
Построение развертки поверхности многогранника сводится к определению натуральной величины каждой его грани. Сначала вычерчивают развертку боковой поверхности, затем к одной из граней присоединяют основания многогранника (одно или два — в зависимости от того, призма это или пирамида
Рис 143.
Практическая работа
Совместно с детьми выполнить и оформить развёртки геометрических тел (рис 143):
· Цилиндра
· Конуса
· Призмы
· Пирамиды.
В ходе построения ещё раз остановиться на особенностях выполнения этой работы. Демонстрировать вырезанные развёртки, показать развёртки выполненные детьми в прошедшие годы.
Подведение итога.
Что вам понравилось на сегодняшнем уроке?