Факультет информатика и управление (ИУ)
Кафедра Информационные системы и телекоммуникации (ИУ-3)
По курсу лекций «Основы теории управления
И цифровая обработка сигналов», 3-й курс, 5-й семестр.
Отчет
по домашнему заданию №1 (ДЗ-1, 2016)
“Проектирование системы управления алгебраическим методом”
Группа ИУ3-52Б, вариант № 14, d0 = 500, Aж = (p2+2ηp+4η2) (p2+4ηp+8η2)
Выполнил: Максименков Ф.Д.
Дата получения задания: 13.09.22
Дата готовности: 01.10.22
Проверил: Коновалов А. В.
Оглавление
Оглавление.......................................................................................................................... 1
1. Цель работы.............................................................................................. 2
2. Техническое задание................................................................................. 2
Содержание работы.......................................................................................................................... 4
1. Определение структуры фильтра с учетом статических требований..... 4
2. Вывод передаточной функции разомкнутой системы в общем виде...... 6
3. Вывод передаточных функций замкнутой системы................................. 7
4. Характеристическое уравнение замкнутой системы................................ 8
5. Желаемое характеристическое уравнение замкнутой системы............... 9
6. Расчет параметров фильтра...................................................................... 9
7. Переходные процессы передаточных функций замкнутой системы..... 10
8. АЧХ W1(p)............................................................................................... 16
9. АЧХ W2(p)............................................................................................... 17
10. ЛАХ и ЛФХ разомкнутой системы..................................................... 18
11. Сопоставление результатов................................................................. 19
12. Выводы:................................................................................................ 20
1. Цель работы.
Освоение алгебраического метода теоретического проектирования автоматических систем управления и регулирования с заданными статическими и динамическими свойствами.
В зависимости от требований Технического задания необходимо выбрать:
· Выбрать структурную схему системы управления.
· Выбрать структуру и параметры фильтра.
· Исследовать статические и динамические свойства системы и доказать их соответствие требованиям Технического задания.
2. Техническое задание.
1. Назначение системы управления.
Система управления предназначена для поддерживания выходного параметра Uвых равным (пропорциональным) управляющему сигналу Uвх и нейтрализации внешних возмущений f, приложенных к объекту.
2. Передаточная функция объекта управления.
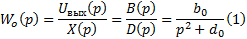
3. Структурная схема системы управления.
|
| Рис. 1 Структурная схема системы управления. |
4. Передаточная функция фильтра произвольного порядка:
Здесь k и v – порядки знаменателя и числителя фильтра соответственно. Структурой фильтра будем называть совокупность этих величин.
5. Суммирующие блоки
Суммирующие блоки в структурной схеме 3. описываются соотношениями:
∆ = Uвх – Uвых (уравнение отрицательной обратной связи).
x = y + f (3)
Совокупность приведенных выше уравнений(2., 4., 5)полностью описывает работу системы управления.
6. Статистические требования к системе управления.
При ступенчатых воздействиях по Uвх и f установившееся значения ошибки ∆ должно быть равно нулю.
7. Динамические требования к системе.
Длительность Т переходных процессов должна быть порядка T ≈ (3…5)/ η, где η – степень устойчивости системы (наименьшая по модулю вещественная часть среди корней характеристического уравнения).
8. Исходные данные, вариант №14.
b0 = 2; η = 10; d0 = 500.
Содержание работы
1. Определим структуру фильтра (величины v и k) с учётом статических требований:
Передаточная функция Wо(p) задана – неизменная часть системы
Здесь m и n –порядки полиномов числителя и знаменателя передаточной функции объекта (4) соответственно;
и 
– известные коэффициенты, причём 
Последовательно с объектом включен корректирующий фильтр с передаточной функцией:
Здесь v и k порядки полиномов числителя и знаменателя 
соответственно
gi и ri– неизвестные коэффициенты, подлежащие определению из статических и динамических требований к системе управления, причём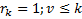 
При заданном объекте попытаемся подобрать такой фильтр, который обеспечивал бы произвольное расположение корней характеристического уравнения замкнутой системы, то есть обеспечивал бы произвольное качество и длительность переходных процессов.
В соответствии со структурной схемой Рис. 1
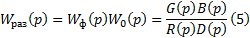
Характеристическое уравнение замкнутой системы – знаменатель передаточной функции, приравненный к нулю:
(7)
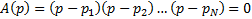(8),
где 
– корни характеристического уравнения 
Порядок N этого уравнения равен сумме порядков полиномов знаменателей передаточных функций объекта (
) и фильтра (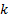
)
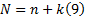
Коэффициенты ajхарактеристического уравнения (7) связаны с корнями pjизвестными формулами Виета
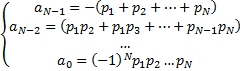(10)
Отсюда (10) видно, что, задав желаемое расположение корней pjможно вычислить желаемое значение коэффициентов aj характеристического уравнения (7) замкнутой системы
В характеристическом уравнении (7) неизвестными являются коэффициенты полиномов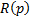 
и 
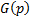, соответственно, знаменатель и числитель передаточной функции фильтра (2)
Приравнивая коэффициенты при одинаковых степенях p, можно получить систему для определения коэффициентов 
и 
фильтра.
Согласно статическим требованиям при ступенчатых воздействиях по Uвх и f установившееся значение ошибки ∆(t) должно быть равно нулю, значит передаточная функция 
должна содержать интегратор (нулевой полюс) с передаточной функцией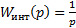 
, то есть должна иметь следующий вид:
Если передаточная функция объекта 
не содержит интегратора, значит интегратор должна содержать передаточная функция корректирующего фильтра . Для выполнения этого условия необходимо равенство 
, тогда
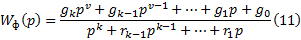
Необходимым условием разрешимости системы уравнений (10) является равенство числа уравнений 
и числа Nф неизвестных (свободных) коэффициентов фильтра, т. е. 
В нашем случае 
(12)
Из равенства 
получим необходимый минимальный порядок 
числителя фильтра: 
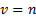
Порядок 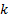знаменателя фильтра произволен, но с учётом реализуемости фильтра: 
Выберем фильтр наименьшего порядка:
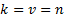(13)
Исходя из выше сказанного, запишем передаточную функцию фильтра в общем виде:
(14)
Объект, заданный выражением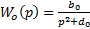 
имеет m = 0 и n = 2 – порядки числителя и знаменателя соответственно, тогда
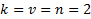(15)
Для заданного объекта Wo(p) запишем выражение для передаточной функции корректирующего фильтра:
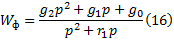
1. Вывод передаточной функции разомкнутой системы в общем виде.
Получим передаточную функцию разомкнутой системы в общем виде
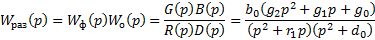
Раскроем скобки и получим:
2. Вывод передаточных функций замкнутой системы.
Получим выражения для передаточных функций замкнутой системы через физические параметры системы:
Числитель и знаменатель передаточной функции полинома объекта - B(p) и D(p) соответственно. Числитель и знаменатель передаточной функции полинома фильтра - G(p) и R(p) соответственно.
Составим систему уравнений на основе структурной схемы (Рис. 1):
(13)
Найдём передаточную функцию замкнутой системы.
Из системы (13) выразим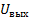 
через 
:
По определению передаточной функции:
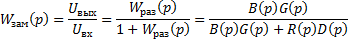
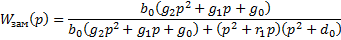
Раскроем скобки и получим:
Найдём передаточную функцию W1(p).
Из системы (13) выразим 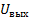через 
:
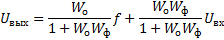
По определению передаточной функции:
Так как знаменатель функции такой же как у 
, изменится только числитель.
Найдём передаточную функцию W2(p).
Из системы (13) выразим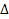 
через :
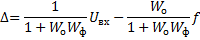
По определению передаточной функции:
Как и в предыдущем случае изменится только числитель.
Определим начальные и конечные значения переходных процессов данных передаточных функций. Начальное значение мы получим, подставив в выражения передаточных функций p = ∞, а установившееся значение, подставив p = 0. Все полученные значения отображены в таблице 1.
Таблица 1. “Начальные и установившиеся значения передаточных функций замкнутой системы”.
| Wзам | W1 | W2 | |
| Начальное значение при p = ∞. | |||
| Установившееся значение при p = 0. |
3. Характеристическое уравнение замкнутой системы.
Построим характеристическое уравнение системы, выраженное через физические параметры и соберём коэффициенты при степенях p
Характеристическое уравнение системы есть знаменатель передаточных функций замкнутой системы, приравненный к 0
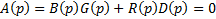
Запишем его с коэффициентами при степенях p.
4. Желаемое характеристическое уравнение замкнутой системы.
Построим желаемое характеристическое уравнение в общем виде, задав его корни. Чтобы система была устойчива, необходимо чтобы действительная часть всех корней была отрицательная. Вариантом задана такая форма характеристического уравнения:
Раскроем скобки и соберем коэффициенты при степенях p:
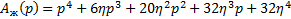
Желаемые корни характеристического уравнения:
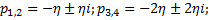
5. Расчет параметров фильтра.
Рассчитаем параметры фильтра при помощи характеристического уравнения.
Запишем характеристическое уравнение замкнутой системы и желаемое характеристическое уравнение.
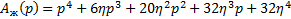
Приравняем коэффициенты при соответствующих степенях p и составим систему уравнений, зависящих от параметров фильтра.
В данной системе неизвестны r1, g0, g1 и g2, а b0, d0 и η заданы вариантом.
b0 = 2; d0 = 500; η = 10.
Решим данную систему и получим:
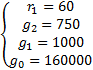
Запишем передаточную функцию фильтра.
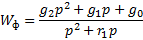
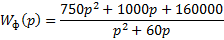
Передаточная функция разомкнутой системы:
6. Переходные процессы передаточных функций замкнутой системы.
Построим переходные процессы для передаточных функций замкнутой системы и определим по ним начальные и установившиеся значения, максимальные отклонения и длительность переходных процессов. Сравним с теоретическими значениями, полученными в п. 3
На рисунках 2 – 4 изображены переходные процессы передаточных функций замкнутой системы.
|
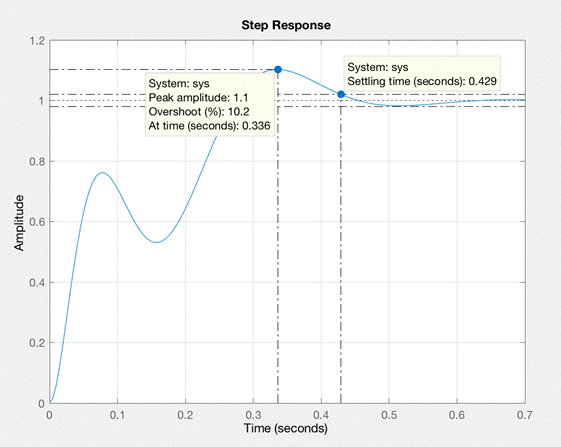
Рис. 2 Переходный процесс для Wзам(p).
Согласно передаточной функции Wзам (p) и по графику h(0) = 0, h(t)уст = 1, h(t)max = 1.1.
Перерегулирование системы составляет 10%:
 .
При точностной трубке 5% (0.95…1.05) относительно h(t)уст = 1 время переходного процесса по графику tр ≈ 0.429.
Теоретически определённое T ≈ (3…5) / η = 0.3…0.5 содержит определенное по графику tp≈ 0.429.
|
|
|
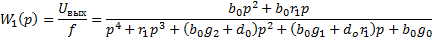
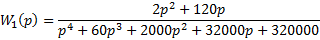
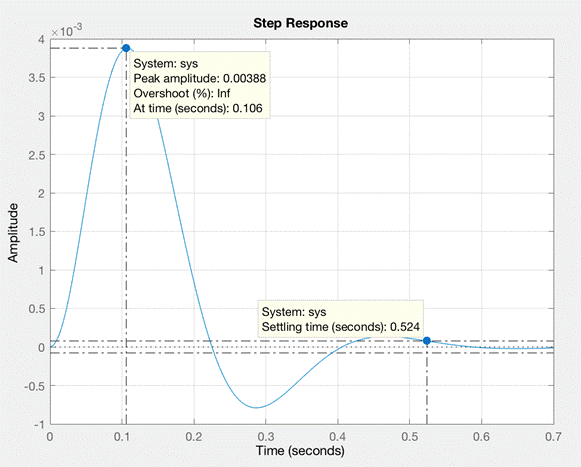
Рис. 3 Переходный процесс для W1(p).
Согласно передаточной функции W1 (p) и по графику h(0) = 0, h(t)уст = 0, h(t)max = 0.00388.
Перерегулирование системы составляет inf:
 .
При точностной трубке 5% (-0,000194…0,000194) относительно h(t)max = 0.00388 время переходного процесса по графику tр ≈ 0.524.
Теоретически определённое T ≈ (3…5) / η = (0.3…0.5) не содержит определенное по графику tp≈ 0.524, но такого же порядка
|
|
|
Рис. 4 Переходный процесс для W2(p).
Согласно передаточной функции W2 (p) и по графику h(0) = 1, h(t)уст = 0, h(t)max = 1.
Перерегулирование системы составляет inf:
 .
При точностной трубке 5% (-0.05…0.05) от h(t)макс = 1 время переходного процесса по графику tр ≈ 0.429.
Теоретически определённое T ≈ (3…5) / η содержит определенное по графику tp≈ 0.429.
|
Начальные и установившиеся значения, максимальные отклонения и длительность переходных процессов отображены в таблице 2.
Таблица 2 “Начальные и установившиеся значения, максимальные отклонения и длительность переходных процессов”.
| Wзам | W1 | W2 | |
| Начальное значение | |||
| Установившееся значение | |||
| Максимальное отклонение | 1.1 | 0.00388 | |
| Время переходного процесса | 0.429 | 0.524 | 0.429 |
Полученные начальные и установившиеся значения полностью совпадают с теоретическими, полученными в пункте 3. Динамические требования системы: T ≈ (3…5) / η. При η = 10 время переходного процесса должно быть одного порядка с 0.3 … 0.5, что соответствует действительности. Из выше сказанного следует, что переходные процессы построены верно.
7. АЧХ W1(p).
Построим амплитудно-частотную характеристику для W1(p) и охарактеризуем её поведение
| Рис. 5 АЧХ W1(p). |
График имеет экстремум в точке (21.7; 0.002381), выходит из начала координат и при 
стремится к 0, что соответствует теоретическим расчетам пункта 3.
8. АЧХ W2(p).
Построим амплитудно-частотную характеристику для W2(p) и охарактеризуем её поведение
|
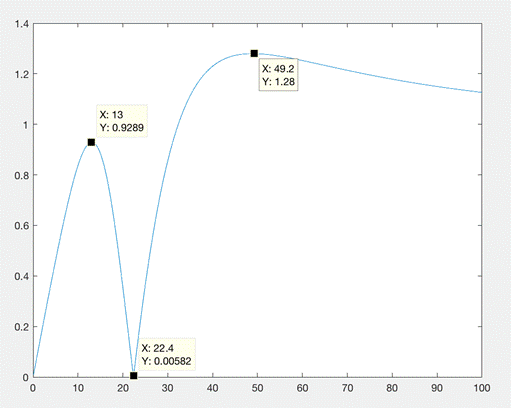
| Рис. 6 АЧХ W2(p). |
График возрастает до экстремума, примерно равного 0,93, на частоте ~13рад/c, а затем падает до 0 на частоте 22.4 рад/с. После график возрастает до второго максимума 49.2 на частоте 1.28 рад/с. Значение в нуле АЧХ равно 0, а на бесконечности равно 1, что соответствует теоретическим расчетам из таблицы 1 пункта 5.
9. ЛАХ и ЛФХ разомкнутой системы.
построим ЛАХ и ЛФХ разомкнутой системы и определим частоту среза, фазу и наклон на частоте среза.
|
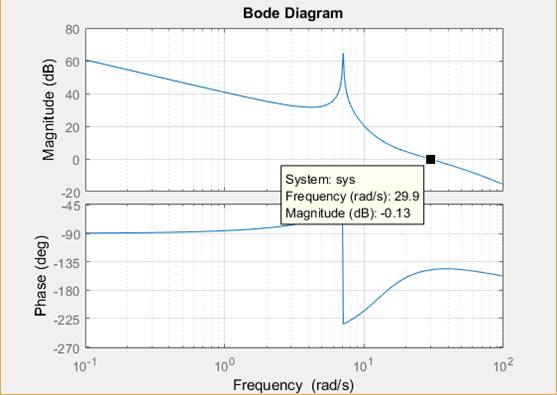
| Рис. 7 ЛАХ и ЛФХ разомкнутой системы. |
Частота среза примерно равна 30 рад/c. Фаза при данной частоте равна примерно -150 градуса. Наклон на частоте среза равен 20 дБ/дек значит переходный процесс в замкнутой системе близок к апериодическому, что соответствует действительности.
10. Сопоставление результатов
Сопоставим в одной таблице параметры переходных процессов и параметры частотных характеристик
|
| 
| 
| ||
| Параметры переходных процессов | Начальное значение | |||
| Установившееся значение | ||||
| Максимальное отклонение | 1.1 | 0.00388 | ||
| Время переходного процесса | 0. 429 | 0.524 | 0.429 | |
| Параметры частотных характеристик | Характерные точки | - | |W1max|=0.007
при ω=19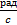 
| |W2max|=1.28
при w=49.2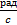
|W2max|=0.93
при w=13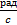
|W2min|=0
при w=22.5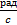
|
| - | |||
| - |
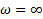
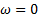
11. Выводы:
Была спроектирована астатическая система управления, отслеживающая входное воздействие и нейтрализующая возмущающее воздействие. передаточная функция фильтра была выбрана исходя из статических и динамических требований системы управления. Теоретически и при моделировании в Simulink:
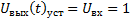и 
Из этого следует, что статические требования к системе управления выполнены.
В работе приведены графики переходных процессов, на основании каждого графика было подсчитано время переходного процесса и перерегулирование. Длительность переходных процессов в системе управления является одного порядка с заданным (T ≈ (3…5)/η=0,3…0,5 c), значит качество переходных процессов считаем удовлетворительным.
Также был проведён анализ построенных амплитудно-частотных характеристик передаточных функций замкнутых систем W1(p) и W2(p) и логарифмические характеристик передаточных функций разомкнутой системы Wраз(p). Начальные и конечные значения АЧХ передаточных функций полностью соответствуют теоретическим расчётам, а наклон в области частоты среза передаточной функции разомкнутой системы составляет -20 дБ/дек. Последнее означает, что замкнутая система стабильна, и переходной процесс в ней близок к апериодическому.