Теоретическая часть
Методы статистические и вероятностные. Методы прогнозирования
Вероятностные методы.
Особенностью информации для проектирования рудников является ее вероятностный характер. Большинство исходных данных для проектирования рудника, принимаемых, как правило, детерминированными, на самом деле являются таковыми лишь с той или иной вероятностью. Поэтому при проектировании широко используется предыдущий опыт уже осуществленных проектов. Например, при проектировании выработки, необходимо определить скорость ее проходки. Можно воспользоваться расчетным методом, основываясь на данных о длительности процессов бурения, заряжания, уборки в натурных условиях.
Пусть мы наблюдаем операцию бурения шпуров определенной глубины. Вот что могло бы получиться в результате.
| Номера шпуров | ||||||||||
| Время бурения, Т, мин |
Для того, чтобы различные величины одного процесса могли быть использованы при проектировании, их сравнивают по степени возможности, числовая характеристика которой называется вероятностью. Для события А формула вероятности записывается следующим образом:
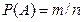, где m- число случаев, когда событие А может произойти, n – общее число случаев.
Событие А называют случайным, а числовую характеристику этого события-случайной величиной.
В нашем примере время бурения шпура – случайная величина.
Очевидно, что вероятность невозможного события равна 0, достоверного – 1, возможного – от 0 до 1.
В нашем случае невозможное событие (2<Т>5), и его вероятность Р(2<Т>5) =0/10=0.
Достоверное событие (2≤Т≤5), и его вероятность Р(2≤Т≤5)= 10/10=1.
|
|
Примером возможного события может быть (2≤Т≤4), и его вероятность Р(2≤Т≤4)= 8/10=0,8
Вот какие вероятности мы можем получить из нашего ряда наблюдений Р(2)=2/10=0,2; Р(3)=4/10=0,4; Р(4)=2/10=0,2; Р(5)=2/10=0,2
Заметим, что сумма вероятностей событий равна 1
Наблюденная информация о случайной или графика плотности распределения.
Случайная величина величине может быть представлена в виде гистограммы, полигона или описана числовыми характеристиками или законом распределения. Числовые характеристики случайной величины – математическое ожидание и дисперсия.
Математическое ожидание случайной величины х, которая может принимать значения х1, х2,…,хк с вероятностью Р1, Р2, …, Рк при дискретном распределении определяется равенством
=0,2*2+0,4*3+0,2*4+0,2*5=3,4, МО характеризует среднее значение случайной величины:
=(3+4+3+5+2+3+4+3+2+5)/10=3,4 Дисперсия характеризует разброс случайной величины от ее математического ожидания
=1.15.
Поскольку размерность дисперсии равна квадрату размерности случайной величины, для оценки разброса используют среднеквадратическое отклонение
Ơх=√D(х)=1,07
Удобной характеристикой случайной величины является коэффициент вариации, который показывает относительный разброс случайной величины
=0,314.
Наиболее полной характеристикой случайной величины является закон ее распределения. Он (ЗР) показывает какова вероятность появления каждого возможного значения СВ. Законов распределения достаточно много. В практике решения задач для горной промышленности часто применяется нормальный закон распределения. Он имеет две формы представления: плотность распределения (дифференциальная функция)
|
|
и функцию распределения (интегральный закон)
dx
С помощью графика плотности вероятностей можно определить: чему равна вероятность того, что что случайная величина Х будет не больше величины А, т.е. Р(Х≤А). Эта вероятность равна заштрихованной площади. Зная Р(Х≤А), нетрудно понять, что СВ Х будет не меньше А, т. е. Р(Х≥А). – (незаштрихованная площадь) Очевидно, что Р(Х≤А)+Р(Х≥А)=1, и Р(Х≥А)=1- Р(Х≤А) В жизни никто эти площади не считает, существуют специальные таблицы.
Вероятностные методы совершенно необходимы для определения достоверности различных данных и показателей, расчетов практически большинства задач проектирования рудника. Они применяются для оценки точности подсчета величины запасов и содержания металлов в руде, при опробовании руд, особенно в условиях сложных рудных месторождений. Широкое применение они находят при исследовании различных стохастических процессов, особенно таких, как выпуск руды из блоков, усреднение и шихтовка руд и т.п. Без вероятностной оценки невозможно правильно решить такие задачи, как обоснование оптимальной величины (нормативов) вскрытых, подготовленных и готовых к выемке запасов, оптимизация календарного плана строительства и эксплуатации рудника. На сложных рудных месторождениях вероятностный подход позволит избежать ошибок при решении такой важной задачи, как определение производственной мощности рудника, вероятностные методы необходимы также при выполнении различного рода прогнозов, которые в деле проектирования имеют большое значение.
|
|
Cтатистические методы.
Статистические методы наиболее часто в практике анализа работы рудников и обогатительных фабрик применяются для установления следующих зависимостей:
- величины капитальных и эксплуатационных затрат на добычу и переработку от производственной мощности предприятия или других важных факторов, в т.ч. горно-геологических;
- показателей обогащения добываемой рудной массы (извлечение в концентраты и содержание в концентратах различных полезных компонентов) в зависимости от содержания в ней полезных и вредных компонентов;
- производительности выпуска руды и погрузочно-транспортных средств в зависимости от степени дробления руды и других факторов;
- выход негабаритов или затраты на вторичное дробление в зависимости от параметров буровзрывных работ и удельного расхода ВВ на отбойку;
- производительности бурения в зависимости от глубины, диаметра скважины и др. факторов.
Применительно к условиям рудников наиболее распространенные эмпирические зависимости, установленные на основе статистических методов, имеют вид линейной, степенной и полиномиальной функций у = а + bх;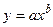 
; 
.
Кроме выбора вида функций необходимо определить входящие в нее постоянные величины а, b и с. Наиболее часто для этого применяется метод наименьших квадратов. Метод наименьших квадратов основан на отыскании минимума суммы квадратов отклонений реальных, полученных опытом, данных от теоретических (расчетных), т.е., когда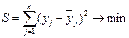 
, где уj - фактические значения исследуемого показателя; 
- расчетные значения, вычисленные по предполагаемому уравнению; n - число реализаций ряда. Например, для линейной функции у = а + bх:
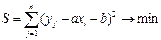
Дифференцируя выражение по а и в и приравняв оба уравнения к 0, получим систему
Решив эту систему, получим искомые коэффициенты уравнения.
После установления характера зависимости и ее параметров должна быть осуществлена весьма ответственная процедура анализа полученной зависимости с точки зрения ее надежности и объективности.
Теснота связи оценивается коэффициентом корреляции
,
Если r=0.6-1.0- связь сильная, r=0,3-0.6 – связь средняя и менее 0.3- связь слабая и недостоверная.
Несмотря на простоту и универсальность статистические методы при проектировании рудников могут применяться лишь в качестве вспомогательных и для решения частных задач. Для обработки данных и выявления эмпирических зависимостей при решении частных вопросов (выбор параметров БВР, определение производительности погрузки, выпуска и доставки, зависимости между потерями и разубоживанием руды, необходимые для нормирования этих показателей использования недр, зависимости между содержанием металлов в добываемых полезных ископаемых и показателями извлечения их при переработке и т.п.).
Методы прогнозирования.
Методы прогнозирования при проектировании рудников применяются для определения основных направлений технического прогресса, вероятного изменения сырьевой базы развития отрасли, производственной мощности рудника и других возможных изменений техники, технологии и технико-экономических показателей рудников в будущем. Использование данных прогноза при проектировании очень важно для выбора прогрессивной технологии и установления технико-экономических показателей.
Прогноз - это вероятностное суждение о состоянии какого-либо объекта (процесса или явления) в определенный момент времени в будущем (или) альтернативных путях достижения каких-либо результатов. Прогнозирование - это процесс формирования прогнозов развития объекта на основе анализа тенденций его развития.
В отличие от планирования при прогнозировании в связи с большими сроками прогнозов имеет место более высокая степень неопределенности вырабатываемой информации.
Основные этапы прогнозирования - это ретроскопия, диагноз (анализ) объекта и проспекция. На стадии ретроскопии осуществляется сбор, хранение, и обработка информации, оптимизация методов измерения и самой информации, на основе чего формируется структура и состав характеристик объекта прогнозирования.
На стадии диагноза осуществляется анализ объекта прогнозирования и составляется прогнозная модель.
При анализе сложного объекта используются теории информации, теория измерений, распознавания образов. Эти методы помогают выбрать важнейшие, ведущие переменные (факторы), минимизировать размерности описания, выбрать адекватные шкалы для измерения количественных и качественных изменений. Математические методы, применяемые при прогнозировании, основаны на теории вероятности и математической статистике, теории численных методов, анализа, теории факторного анализа.
Наиболее распространенными методами прогнозирования являются экстраполяционные (сглаживания и уравнивания статистического ряда, экстраполяция простыми зависимостями с использованием степенных полиномов, экстраполяция тенденций по огибающим кривым и др.), статистические (корреляционный и регрессионный анализы, факторный анализ), экспертные, переработки патентной информации, технологического моделирования и др.
По степени детерминированности можно выделить объекты:
1) детерминированные, в которых случайной составляющей можно с достаточной точностью пренебречь;
2) стохастические, в описании которых необходим учет случайной составляющей переменных в соответствии с требуемой точностью и задачей прогноза;
3) cмешанное, имеющее характеристики детерминированные и стохастические.
Какой-либо процесс или показатель можно представить в виде переменного ряда Уt выражением
Уt = Xt + et
где Хt - детерминированная составляющая процесса (тренд); et - случайная (стохастическая) составляющая процесса.
Прогнозное значение величины Уt определяется суммой прогнозных значений тренда и случайной составляющей. Если известна функция тренда, то задача определения детерминированной составляющей решается. Если неизвестна, то надо установить подходящий для данной задачи вид тренда. Обычно из ряда функций, представляющих собой прямые, параболы, степенные функции и т.п. наиболее простым и распространенным методом является метод наименьших квадратов, ранее рассмотренный.
При прогнозировании применяются также методы экспоненциального сглаживания, метод скользящей средней и др.
Нормирование величины вскрытых, подготовленных и готовых к выемке запасов.
Для того чтобы рудник работал ритмично и выполнялась производственная программа по добыче руды в определенном количестве и качестве, необходим резерв вскрытых, подготовленных и готовых к выемке запасов.
По степени подготовленности к выемке запасы обычно делят на три категории:
1) вскрытые;
2) подготовленные;
готовые к выемке.
Вскрытые - это запасы, к которым пройдены все основные вскрывающие выработки (стволы, околоствольные дворы, квершлаги и т.п.), позволяющие начать проведение подготовительно-нарезных выработок (штреков, восстающих, ортов, буровых и транспортных выработок, выработка днища и блока и т.п.).
Подготовленные - это запасы, к которым пройдены все подготовительные выработки (штреки, восстающие, орты) позволяющие начать нарезные работы в блоках (камерах) (буровые и транспортные выработки, выработки днища блоков и т.п.).
Готовые к выемке запасы - это запасы блоков (камер), в которых пройдены все подготовительно-нарезные выработки и выполнены другие работы (разбуривание блоков, установка виброкомплексов, выполнение массовых взрывов, ликвидация их последствий и др.), позволяющие начать в любой момент очистную выемку руды (непосредственно выдачу руды из очистных забоев).
Итак, наименьшая технологическая единица, которой оперируют при определении запасов по степени подготовленности к выемке – эксплуатационный блок.
В литературе можно встретить термин "выемочная единица". Это - "минимальная часть запасов полезного ископаемого, отрабатываемая одной системой разработки, при выемке которой осуществляется полный цикл отработки.
Далее будем оперирировать и понятием «блок»и понятием«выемочная единица», имея в виду, что это одно и то же.
Блок или выемочная единица характеризуются горно-геологическими, техническими и организационными параметрами, которые используются при определении величины подготовленных запасов.
К горно-геологическим параметрам относятся: геометрические размеры выемочной единицы; элементы залегания рудного тела в границах выемочной единицы; балансовые запасы руды и содержание в ней полезных компонентов; извлекаемые запасы горной массы и содержание в ней полезных компонентов.
К техническим параметрам выемочной единицы относятся: размеры выработок; количество стадий отработки; объемы работ по стадиям выемки; длительность допустимого совмещения отдельных стадий отработки и ограничения на совмещение в пространстве; производительность машин и механизмов, работающих в выемочной единице; скорости проведения подготовительно-нарезных выработок и интенсивность очистной выемки; порядок, направление и очередность отработки выемочной единицы в пределах этажа и шахтного поля по простиранию и падению рудного тела.
К организационным параметрам относятся: режим работы рудника; график отработки выемочной единицы.
Основные требования, которые необходимо учитывать при определении запасов различной степени подготовленности к выемке, могут быть сведены к следующим положениям.
1. Запасы различной степени подготовленности к выемке создаются на базе разведанных запасов месторождения в пределах шахтного поля с целью обеспечения заданной производительности подземного рудника и сосредоточены в эксплуатационных блоках, находящихся одновременно в стадиях подготовки, нарезки и очистной выемки;
2. Соотношение запасов различной степени подготовленности находится в зависимости от длительности периодов полного цикла отработки выемочной единицы, схемы развития горных работ и ограничений, накладываемых существующим порядком отработки шахтного поля;
3. В условиях действующего рудника запасы различной степени подготовленности к выемке должны определяться с учетом влияния осложняющих факторов (изменчивость горно-геологических условий, отказы в работе выемочных единиц), предусматривая целесообразный резерв выемочных единиц.
Из определения, данного выше, следует, что запасы по степени подготовленности к выемке находятся в действующих выемочных единицах, обеспечивающих производительность рудника по проведению подготовительных, нарезных выработок и очистной выемке.
N = Nп + Nн + Nо,
где Nп, Nн, Nо - количество выемочных единиц в одновременной работе в периодов подготовки, нарезки, очистной выемки.
Полный цикл отработки блока включает периоды подготовки, нарезки и очистной выемки.
Т = Тп + Тн + То,
где Тп, Тн, То - продолжительность периодов подготовки, нарезки и очистной выемки.
Количество действующих блоков при заданной производительности рудника Ар определяется, исходя из продолжительности полного цикла отработки T и запасов руды, извлекаемых из блоков в течение этого цикла - qeN
где qe - извлекаемые запасы выемочной единицы.
Из приведенной формулы видно, что величина запасов различной степени подготовленности зависит от извлекаемых запасов выемочной единицы, состава, объемов и интенсивности работ, осуществляемых в течение цикла отработки.
Непрерывность и ритмичность развития фронта горных работ обеспечивается соотношением выемочных единиц в стадиях подготовки, нарезки и очистной выемки. Математическое выражение этого соотношения следующее
Если очистные работы выполняются в несколько очередей, то количество выемочных единиц, находящихся в одновременной выемке камер и целиков рассчитывается по формулам:
; 
где Nок, Nоц - количество соответственно камер и целиков; Tок, Tоц - длительность отработки соответственно камер и целиков.
Количество выемочных единиц в одновременной подготовке и нарезке равно:
; 
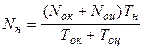Если после выемки камер предусматривается их закладка, должно соблюдаться соотношение
где Nзк - количество камер в закладке.
Итак, вскрытые запасы сосредоточены в блоках, находящихся в стадиях подготовки, нарезки и очистной выемки. Кроме того, рудник может иметь некоторое количество вскрытых запасов Qв1, сосредоточенное на участках, в которых горные работы не ведутся
Qв =(qп+qн+qо)*Nп +(qн+qо)*Nн+qо*Nо+ Qв1,
Подготовленные запасы сосредоточены в блоках, находящихся в стадиях нарезки и очистной выемки
Qп =(qн+qо)*Nн+qо*Nо,
Готовые к выемке запасы сосредоточены в блоках, находящихся в стадии очистной выемки
Qг =qо*Nо,
В этих формулах запасы по степени подготовленности рассчитаны в единицах массы, т. е. в тоннах.
Кроме этого запасы могут быть преставлены в единицах времени. Например количество готовых к выемке запасов в единицах времени равно
Тг =qо*Nо / Ар,
Где Ар – месячная производительность рудника,т.;
Запасы подготовленныек выемке:
Тп =((qн+qо)*Nн)/ Ар)+ qо*Nо / Ар.
То есть, выражение обеспеченности той или иной категорией запасов в единицах времени показывает, на сколько месяцев хватит запасов для обеспечения заданной производительности рудника.
Рассмотрим процесс образования запасов той или иной степени подготовленности на примере запасов, подготовленных к выемке (рис).
Рис. График движения запасов.
При развитии работ на горизонте от центра к флангам в начале количество подготовленных запасов равно запасам блока в стадиях нарезки и очистной выемки. Затем, по мере продвижения нарезных работ подготовленные запасы уменьшаются со скоростью производительности нарезки. При включении следующих блоков в работу количество подготовленных запасов будет расти и достигнет максимума при полном развитии активного фронта горных работ. Колебания запасов будут в пределах величины запасов блока или группы блоков, вводимых одновременно в работу. При других схемах развития горных работ колебательный характер движения запасов также будет иметь место, но период и амплитуда колебаний будут отличаться.
Практическая часть