В процессе истечения потенциальная энергия жидкости, находящейся в резервуаре, пере-ходит в кинетическую энергию струи.
Основным вопросом, который изучается в данном случае, является определение скорос-ти истечения и расхода жидкости при постоянном и переменном напоре из отверстий и насад-ков различных форм.
5.1. Истечение через малое отверстие в тонкой стенке
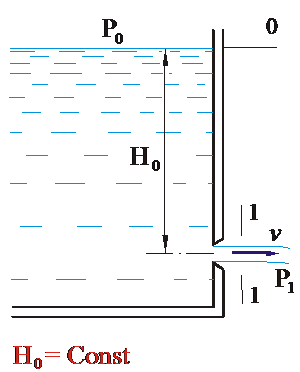
Рассмотрим большой резервуар с жидкостью под дав-лением Р 0, имеющий малое отверстие в стенке на глубине Н 0 от свободной поверхности (рис. 5.1).
Рис. 5.1.
Истечение из резервуара
через малое отверстие
Составим уравнение Бернулли для сечений 0-0 и 1-1
(плоскость сравнения проходит по оси струи):
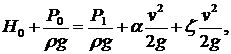
и приведем его к виду:
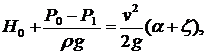(5.1)
где ζ – коэффициент местного сопротивления отверстия (путевыми потерями пренебрегаем).
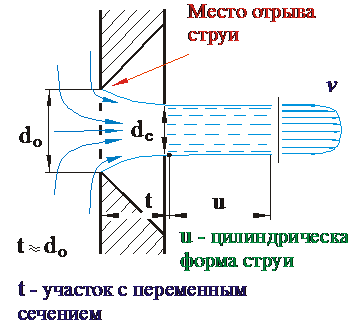Рассмотрим структуру потока непосредственно перед отверстием и струи на выходе из него, рис. 5.2.
Рис. 5.2.
Схема истечения через круглое отверстие с разделанной кромкой
Сжатие струи от диаметра d о (отверстия)до диа-метра d с (струи) обусловлено скоростным давле-нием пристеночных слоев жидкости перед от-верстием при переходе от радиального направ-ления течения к осевому движению в струе.
Такое изменение формы струи называется «совершенным сжатием».
Степень сжатия оценивается коэффициентом сжатия ε:
ε = s с / s о =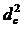 
/ 
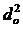. (5.2)
В выражении (5.1)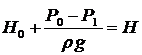 
. Н – это расчетный напор. Пусть Р 0 – атмосферное давление, тогда: Р 0 = Р 1 и Н 0 = Н.
Окончательно получаем: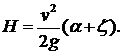 
(5.3)
Из выражения (5.3) определяем скорость истечения струи:
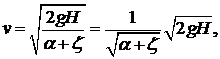(5.4)
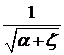= φ – коэффициент скорости струи.
Для идеальной жидкости: ζ = 0, α = 1. Тогда φ = 1, а скорость истечения будет равна: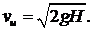 
Для реальной жидкости: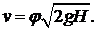 
(5.5)
Из формулы (5.5) получаем: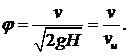 
Коэффициент φ равен отношению скоростей истечения реальной и идеальной жидкостей. Он всегда меньше единицы.
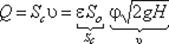Расход жидкости определяется как произведение действительной скорости истечения на фак-тическую площадь сечения струи S с:
Произведение ε и φ обозначают буквой μ и называют коэффициентом расхода:
μ = εφ.
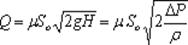Произведя замену εφ на μ получаем:
(5.6)
где Δ Р – разность давлений, под действием которой происходит истечение.
Выражение (5.6) – это основная формула для определения расхода жидкости.
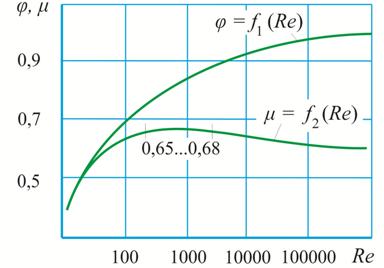Значение коэффициентов скорости φ и расхода μ для круглого отверстия можно определить по графикам, показанным на рис. 5.3.
Рис. 5.3. Зависимости φ и μ для круглого
отверстия в тонкой стенке от числа
Рейнольдса.
Для маловязких жидкостей – воды, бензина, спирта и др. при Re > 104, можно принимать μ = 0,62.
5.2. Истечение при несовершенном сжатии
Несовершенное сжатие происходит при истечении через отверстие, когда на формирование струи оказывают влияние боковые стенки резервуара, рис. 5.4.
Рис. 5.4.
Схема несовершенного сжатия струи
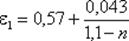Здесь струя на выходе из отверстиясжимается в меньшей степени, так как стенки не дают об-разоваться радиальным течениям.
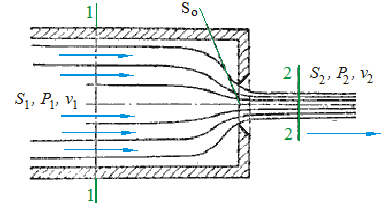
Коэффициент сжатия для данного случая определяют по формуле Жуковского:
где n – отношение площади отверстия s о к площади поперечного сечения резервуара s 1:
n = s о / s 1.
Коэффициент расхода будет равен: μ 1 = ε 1 φ,
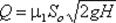
а расход жидкости при несовершенном сжатии: (5.7)
При этом напор Н следует определять с учетом скоростного напора в резервуаре:
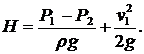
5.3. Истечение через насадки при постоянном напоре
Истечение через насадок может происходить в двух режимах.
Первый режим – безотрывный. На входе в насадок струя сжимается, но при взаимодействии с вихревой зоной – расширяется до размеров насадка, рис. 5.5.
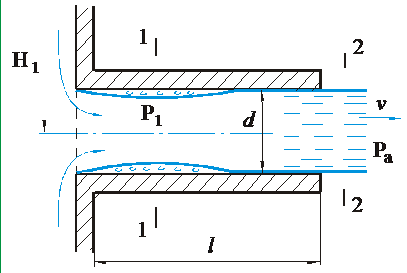
Рис. 5.5.
Истечение через цилиндрический насадок
В этом случае на выходе из насадка ε = 1 и μ = φ. При Re > 10 000, μ ≈0,8.
Коэффициент расхода μ зависти еще и от отношения l / d, рис. 5.6.
Рис. 5.6.
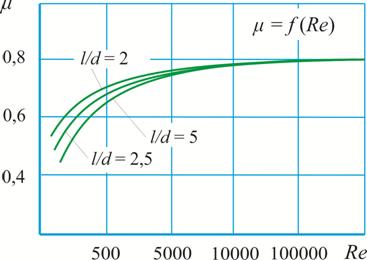Зависимость коэффициента расхода внешнего цилиндрического насадка Re
Расход увеличивается из-за отсутствия сжатия струи, поэтому коэффициент μ увеличивается от 0,62 до 0,8.
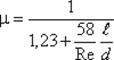Коэффициент расхода μ определяется по эмпи-рической формуле:
(5.8)
Формула описывает кривые асимптотического характера, поэтому при Re → ∞, μ = μ max = 0,813.
При l / d < 1 (короткий насадок) – имеет место второй отрывный режим истече-ния, в котором струя после сжатия сохраняет цилиндрическую форму и не соприкасается со стенками, рис. 5.7.
Рис. 5.7.
Второй режим истечения через насадок
Истечение становится таким же, как и из отверстия в тонкой стенке. При этом μ = 0,62.
5.4. Истечение через соплó (коноидальный насадок)
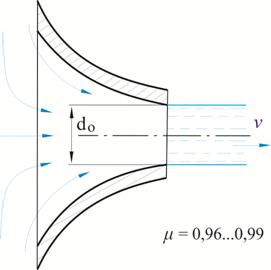
Сопло обеспечивает безотрывность течения и параллель-ноструйность в выходном сечении, рис. 5.8.
Сопло имеет коэффициент сжатия струи ε =1, коэффициент расхода μ = 0,96…0,99.
Рис. 5.8.
Истечение через сопло
5.5. Истечение через диффузорный насадок
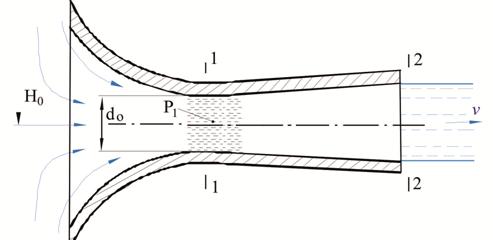Диффузорный насадок – это сочетание сопла и диффузора, рис. 5.9.
Рис. 5.9.
Истечение через диффузорный насадок.
Приставка диффузора создает узкое место. При течении жид-кости через сужение (аналог – труба Вентури) скорость потока возрастает, давление Р 1 падаетниже атмосферного, создается всасывающий эффект и жид-кость вытекает быстрее.
Можно достигнуть увеличения расхода в 2…2,5 раза.
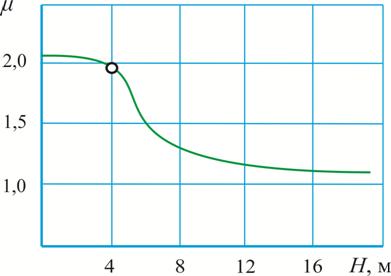
На рис. 5.10 показана зависимость коэффициента расхода от напора.
Рис. 5.10.
Зависимость коэффициента расхода от напора
Но этот эффект проявляется при Н = 4 м. и меньше. При бóльшем напоре развивается кавитация и коэффициент расхода резко снижается.
5.6. Истечение жидкости при переменном напоре
Рассмотрим случай опорожнения сосуда при постоянно уменьшающемся напоре h.
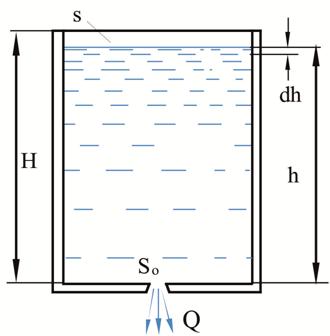Особенность такого истечения состоит в том, что расход жидкости через отверстие яв-ляется переменным, а течение – нестационарным, рис. 5.11.
Рис. 5.11. Схема истечения при переменном напоре
Но если скорость истечения инапор изменяются медленно, то движение в каждый момент времени можно рассматривать как квазистационарное.
Обозначим dh - изменение уровня жидкости за бес-конечно малое время dt. Тогда можно записать сле-дующее уравнение объемов: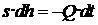 
или:
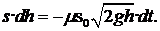
Знак минус обусловлен тем, что положительному приращению времени dt соответствует
отрицательное приращение уровня dh.
Выразим время dt: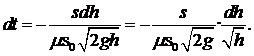 
(5.9)
Чтобы найти время истечения (полное время опорожнения сосуда), проинтегрируем вы-ражение (5.9) по времени:
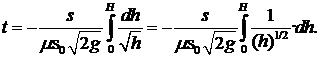(5.10)
Воспользуемся табличным интегралом: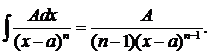 
В нашем случае: А = 1, а = 0, n = 1/2.
Из выражения (5.10) получаем:
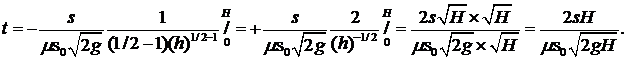(5.11)
Итак, время полного опорожнения сосуда равно: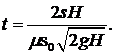 
(5.12)
2 sН – это удвоенный объем полного сосуда,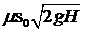 
– расход жидкости через отверстие при постоянном уровне h = H = Const.
Время вытекания жидкости объемом sH при H = Const равно: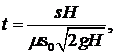 
следовательно, этот же объем при переменном уровне будет вытекать в 2 раза дольше.
5.7. Взаимодействие струи с твердыми поверхностями
Рассмотрим случай воздействия струи на коническое тело, рис. 5.12.
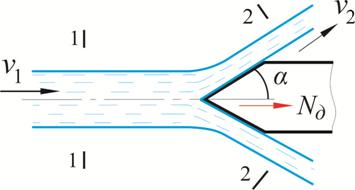
Рис. 5.12. Схема действия струи на
коническое тело
Сечение 2-2 не плоское, а в виде конического кольца.
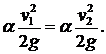Составим уравнение Бернулли для сечений 1-1 и 2-2: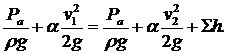 
Если пренебречь потерями, то можно записать равенство:
Из чего следует, что скорости v 1 и v 2 равны.
Уравнение расходов: Q 1 = Q 2 дает равенство: Q = v 1 s 1 = v 2 s 2,
где s 1 и s 2 – площади сечений 1-1 и 2-2. Если равны скорости, то равны и площади.
Теперь рассмотрим равенство: Qρv = Q m v,(5.13)
где Q – расход жидкости в струе (м3/с), ρ – плотность жидкости (кг/м3), v – скорость потока в струе (м/с), Q m – массовыйрасход жидкости в струе (кг/с).
Q m v – это гидравлический аналог количества движения – количество движения потока (кг/с×м/с → кг·м/с2).
Количество движения в механике это произведение массы на скорость; имеет размер-ность кг·м/с.
Количество движения потока имеет размерность силы (Н).
Количество движения потока, как векторная величина, равно:
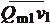- в сечении 1-1:
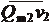
- в сечении 2-2:
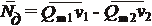Сила динамического давления струи определяется как векторная разность:
Как скалярная величина, cила давления определится выражением:
Nд = Q m1· v 1 – Q m2· v 2· Cosα = Q m· v (1 – Cosα) (5.14)
Сила давления струи возникает потому, что количество движения потока изменяется по нап-равлению.
Рассмотрим механический аналог.
Если тело движется прямолинейно с постоянной скоростью, то количество движения не изме-няется. Скорость не меняется, направление прежнее, поэтому сила не возникает.
Если тело вращается вокруг оси, то по значению количество движения не изменяется, но из-меняется векторно. Поэтому и возникает сила, действующая на связь, которая удерживает тело.
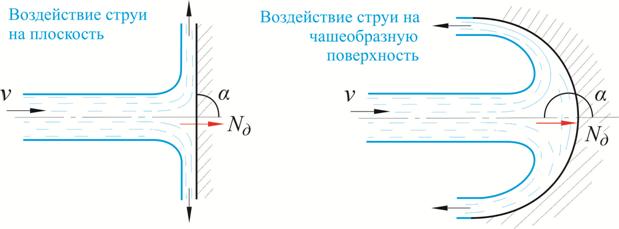
Рис. 5.13. Действие струи на плоскую и полусферическую преграды
Для плоской преграды угол α равен 90º, а Cos 90 = 0, поэтому из формулы (5.14):
Nд = Q m· v (1 – Cosα)
получаем равенство: Nд = Q m· v.
Так как Cos 180 = – 1, то сила динамического давления равна: Nд = Q m· v (1 + 1) = 2 Q m· v.