Реферат
на тему:
"Решение систем дифференциальных уравнений"
Дифференциальная линейная алгебра
С собственными значениями и векторами матрицы приходится иметь дело в задачах, связанных с решением систем линейных дифференциальных уравнений и исследованием устойчивости этих решений. Дифференциальная векторно-матричная алгебра включает в себя операции интегрирования и дифференцирования, которые во множестве случаев в своей нотации напоминают соответствующие операции обычного дифференциального исчисления. Производная по скалярной переменной и интеграл от вектора и матрицы в заданных пределах изменения скалярной переменной определены так:
Производные от векторных и векторно-матричных выражений определяются следующими правилами:
,
,
,
,
.
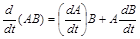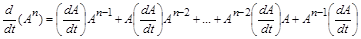2. Векторное решение однородного уравнения
Пусть система линейных однородных дифференциальных уравнений задана в векторной форме:
Если уравнение записано в форме однородного дифференциального уравнения n -го порядка и его характеристический многочлен имеет различные корни, то общее решение представляется суммой n частных решений с экспоненциальными базовыми функциями:
,
где 
– константы, определяемые начальными условиями.
Можно предположить, что векторное уравнение, представляющее общее решение, имеет аналогичную форму
.
Для выяснения вопроса, что есть в таком представлении 
и 
, подставим частное решение 
в уравнение:
Отсюда видно, что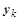 
будет частным решением, если 
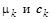будут собственным значением и собственным вектором матрицы A.
Таким образом, если матрица A имеет собственные значения и векторы 
, k=1,2,…, n, то общее решение однородного векторного уравнения после ряда эквивалентных преобразований предстанет в следующем виде:
|
|
.
Используя значение решения при t= 0, находим 
. Таким образом, общее решение однородного векторного уравнения имеет следующий вид: 
.
Матричная экспонента выражается через проекторы и собственные значения матрицы по формулам спектрального разложения:
.
После подстановки X в решение вместо экспоненты получим:
.
В случаях, когда собственные значения и векторы найти не удается, матричную функцию можно разложить в ряд по степеням матрицы:
,
что позволяет численно получать многомерный переходной процесс, если ряд сходится.
Матричный ряд сходится, если существует предел последовательности частичных сумм. Достаточным условием является сходимость ряда из норм членов степенного матричного ряда. Используя, например, признак сходимости Даламбера ряд, представляющий матричную экспоненту, сходится, если существует и меньше единицы предел отношения
,
где R – радиус сходимости.
Объем вычислительной работы при оцифровке многомерного переходного процесса существенно зависит от числа членов в матричном ряде. Для повышения скорости сходимости применяют различные аппроксимации этого ряда. В частности, для экспоненты широко используются аппроксимации отрезков ряда дробно-рациональными функциями Падэ вида:
.
Так, матричная экспонента для трех и четырех членов имеет вид:
|
|
В свете приведенных разложений матричной экспоненты общее решение линейного векторно-матричного дифференциального уравнения приближенно можно вычислить по формуле:
.