Определение 13.3. Точка графика непрерывной функции, отделяющая ее выпуклую часть от вогнутой (см. рис. 13.5), называется точкой перегиба.
Рисунок 13.5. График функции, имеющий перегиб в точке 
Замечание 13.2. Точкой перегиба может быть только та точка, в которой к кривой имеется касательная. В окрестности точки перегиба кривая лежит по обе стороны от касательной: выше и ниже ее. Заметим, что она расположена также по обе стороны от нормали (см. рис. 13.6).
Но такая точка, как Р (см. рис. 13.6), в которой единственной касательной не имеется, точкой перегиба не является.
Рисунок 13.6. Точки перегиба 
и 
.
Точка 
не является точкой перегиба
Замечание 13.3. Приведенные определения выделяют возможные расположения кривой графика функции относительно касательной к ней в достаточно малой окрестности точки касания. Поэтому не следует думать, что приведенные определения исчерпывают все возможные случаи такого расположения. Например, для функции
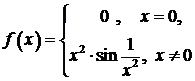
ось 
пересекает и касается графика функции в точке 
но точка 
не является точкой перегиба для графика этой функции.
Теорема 13.3. (достаточное условие существования точки перегиба).
Пусть функция 
имеет вторую производную 
в некоторой окрестности точки 
. Если вторая производная меняет знак при переходе аргумента через точку х0, то точка с координатами 
является точкой перегиба графика функции.
Доказательство. Пусть, например, 
в интервале 
и 
в интервале 
, где 
– положительное число. В этом случае график функции в интервале – выпуклый, а в интервале – вогнутый. Следовательно, точка с координатами является точкой перегиба графика функции, что и требовалось доказать.
Теорема 13.4. (необходимое условие существования точки перегиба).
Пусть функция имеет в интервале 
непрерывную вторую производную и точка 
является абсциссой точки перегиба графика данной функции. тогда 
.
Доказательство. Предположим противное. Пусть 
и для определенности, например, 
. Тогда в силу непрерывности второй производной в точке получим, что в некоторой окрестности точки х0. Следовательно, в этой окрестности график вогнутый, но это противоречит тому, что х0 – абсцисса точки перегиба. Следовательно, предположение неверное. Полученное противоречие доказывает теорему.
Замечание 13.3. Могут встретиться случаи, когда в точке х0 вторая производная непрерывной функции не существует, однако эта точка является абсциссой точки перегиба.
Например, функция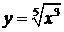 
, определенная для 
, имеет вторую производную 
.
В точке вторая производная 
не существует. Однако если 
, то получаем, что 
, а если 
, то имеем 
. Следовательно, точка (0; 0) является точкой перегиба.
Определение 13.4. Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками второго порядка функции.
Не все критические точки второго порядка функции являются абсциссами точек перегиба графика функции.
.
Вторая производная 
дважды дифференцируемой функции в точке перегиба 
равна нулю, то есть 
= 0.
Если вторая производная при переходе через некоторую точку меняет свой знак, то является точка перегиба ее графика.
Отсюда следует правило нахождения точек перегиба:
1) найти вторую производную данной функции;
2) приравнять ее нулю и решить полученное уравнение (или найти те значения х, при которых производная теряет числовой смысл), из полученных корней отобрать действительные и расположить их no величине от меньшего к большему;
3) определить знак второй производной в каждом, из промежутков, отграниченных полученными корнями;
4) если при этом в двух промежутках, отграниченных исследуемой точкой, знаки второй производной окажутся разными, то имеется точка перегиба, если одинаковыми, то точки перегиба нет.