Теорема 4.2. Если члены сходящегося ряда, не меняя их порядка, объединить в конечные группы и составить ряд из сумм этих групп, то полученный будет сходиться и его сумму равняется сумме первоначального ряда.
Эту теорему можно коротко формулировать так: члены сходящегося ряда можно заключать в скобки. Еще иначе можно сказать, что сходящиеся ряды обладают "сочетательным свойством".
Интересно отметить, что из сходимости ряда, члены которого заключены в скобки не вытекает сходимость исходного ряда. Это видно хотя бы из следующего примера: хотя ряд [1 + (-1)] + [1 + (-1)] + [1 + (-1)] +...сходится, но ряд 1 + (-1) + 1 + (-1) + 1 +...расходится.
Таким образом, "раскрывать скобки" можно не всегда.
Теорема 4.3. Если все члены сходящегося ряда умножить на одно и то же число, то вновь полученный ряд будет сходиться, и его сумма будет равна сумме первоначального ряда, умноженной на то же число.
Теорема 4.4. Сходящиеся ряды можно почленно складывать.
Остаток ряда
Определение 4.4.
Если 
, (4.1)
есть некоторый ряд, и 
– какое-нибудь натуральное число, то остатком ряда (4.1) после m -го члена называется ряд 
Теорема 4.5. Сам ряд и его остаток сходятся или расходятся одновременно.
Доказательство. Пусть 
и 
– частичные суммы ряда (4.1), а 
–частичная сумма остатка этого ряда. Тогда 
при n > m.
Пусть остаток ряда (4.1) сходится и его сумма равна 
. Тогда при стремлении n к бесконечности будет выполняться: 
. Отсюда следует, что 
. Получили, что ряд (4.1) сходится и его сумма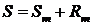 
. Обратно, если сходится ряд (4.1) и сумма его равна S, то из соотношения вытекает, что и . Следовательно, ряд (4.1) сходится и его сумма 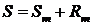, что и требовалось доказать.
Теорема 4.6. Сумма остатка сходящегося ряда после m -го члена стремится к нулю при возрастании .
|
|
Это следует, из того, что если ряд (4.1) сходится, то из равенства 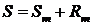вытекает, что – сумма его остатка после m -го члена равна разности между суммой S всего ряда и его частичной суммой 
. При возрастании m частичная сумма Sm будет стремиться к S, то отсюда следует 
, что и требовалось.
Знакоположительные ряды
Определение 4.5.
Если задан числовой ряд (4.1)
и все члены ряда 
(n = 1, 2, 3,...), то ряд (4.1) называется положительным. Если 
для всех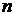 
, то ряд (4.1) называется строго положительным.
Частичная сумма положительного ряда (4.1) с увеличением n возрастает (может быть, не строго).
Таким образом, как всякая возрастающая числовая последовательность, последовательность частичных сумм 
имеет конечный или бесконечный предел, т.е. для любого положительного ряда существует предел 
. Отметим еще, что частичные суммы сходящегося положительного ряда не превосходят его суммы.
Этот предел может быть конечным или бесконечным в зависимости от ограниченности сверху последовательности частичных сумм .
Теорема 4.7. Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху.
Теорема 4.7 сводит вопрос о изучении сходимости положительного ряда к более простому вопросу, а именно к вопросу об ограниченности последовательности его частичных сумм.
Признаки сравнения
Рассмотрим два положительных числовых ряда 
и 
.