Если предел отношения общих членов п оложительных рядов  и
и  равен конечному, отличному от нуля числу
равен конечному, отличному от нуля числу  :
:  , то оба ряда
, то оба ряда  и
и  сходятся или расходятся одновременно, т.е из сходимости ряда
сходятся или расходятся одновременно, т.е из сходимости ряда  следует сходимость ряда
следует сходимость ряда  , а из ра сходимости ряда
, а из ра сходимости ряда  следуетра сходимость ряда
следуетра сходимость ряда  .
.
Замечания:
1) Если речь идёт о двух сходящихся рядах  и
и  , то предел отношения общих членов может быть равен и нулю (но не бесконечности);
, то предел отношения общих членов может быть равен и нулю (но не бесконечности);
2) если речь идёт о двух расходящихся рядах  и
и  , то предел отношения общих членов может быть равен и бесконечности (но не нулю);
, то предел отношения общих членов может быть равен и бесконечности (но не нулю);
3) п редельный признак сравнения применяется тогда, когда общие члены рядов являются отношением многочленов от 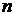 . Либо один или оба многочлена также могут находиться под корнем;
. Либо один или оба многочлена также могут находиться под корнем;
4) не имеет значения, в каком порядке составлять отношение общих членов при использовании предельного признака сравнения, можно было составить  – это не изменило бы сути дела.
– это не изменило бы сути дела.
Довольно часто числовой ряд сравнивают с известными гармоническим и обобщенно-гармоническим рядами.
Пример 11. Исследовать на сходимость ряд 
Решение. Общий член ряда 
Используем первый признак сравнения рядов. Для сравнения удобно выбрать сходящийся ряд, например, бесконечно убывающую геометрическую прогрессию:  со знаменателем
со знаменателем  .
.
Из сравнения общих членов рядов  и
и  имеем
имеем  . Получили
. Получили  и ряд
и ряд  сходится. Следовательно, по первому признаку сравнения заданный ряд тоже сходится.
сходится. Следовательно, по первому признаку сравнения заданный ряд тоже сходится.
Пример 4.6. Исследовать на сходимость ряд 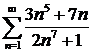 .
.
Преобразуем общий член ряда  . Сравним данный ряд со сходящимся рядом
. Сравним данный ряд со сходящимся рядом  . Применяем предельный признак сравнения.
. Применяем предельный признак сравнения.
 .
.
Вывод: предел отношения общих членов п оложительных рядов  и
и  равен конечному числу
равен конечному числу  , ряд
, ряд  – сходится, значит, исследуемый ряд
– сходится, значит, исследуемый ряд  тоже сходится. Ответ: ряд сходится.
тоже сходится. Ответ: ряд сходится.
Если бы для сравнения был выбран другой ряд, а не ряд  , из совокупности обобщенно-гармонических рядов, то не получилось бы в пределе отношения общих членов конечного, отличного от нуля, числа.
, из совокупности обобщенно-гармонических рядов, то не получилось бы в пределе отношения общих членов конечного, отличного от нуля, числа.
Пример 4.7. Исследовать на сходимость ряд 
Решение. Общий член ряда  . Применим предельный признак сходимости. В качестве ряда
. Применим предельный признак сходимости. В качестве ряда  возьмем обобщенно-гармонический ряд с показателем
возьмем обобщенно-гармонический ряд с показателем  . Ряд
. Ряд  – расходится.
– расходится.
Рассмотрим 
Следовательно, ряды  и
и  сходятся и расходятся одновременно. Ряд
сходятся и расходятся одновременно. Ряд  – расходится, поэтому и ряд
– расходится, поэтому и ряд  тоже расходится.
тоже расходится.
Лемма 4.1. Если члены строго положительного ряда (4.1) при всех номерах n удовлетворяют неравенству:  ,
,
где q - некоторое постоянное число, меньшее единицы: 0 < q < 1,
то ряд (4.1) сходится.
Доказательство. Действительно, по условию
 .
.
Перемножая эти неравенства и сокращая, получим:  .
.
Тогда  . Это говорит о том, члены ряда (4.1) не больше соответствующих членов ряда
. Это говорит о том, члены ряда (4.1) не больше соответствующих членов ряда  , т.е.
, т.е.
 =
=

Множитель в скобках представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем  . Прогрессия – сходится. Но тогда сходится и ряд (4.1).
. Прогрессия – сходится. Но тогда сходится и ряд (4.1).
Замечание. Неравенство  еще не обеспечивает сходимости ряда (4.1). Это видно хотя бы на примере гармонического ряда
еще не обеспечивает сходимости ряда (4.1). Это видно хотя бы на примере гармонического ряда  .
.
Признак Даламбера
Теорема 4.8. Пусть ряд (4.1) –строго положительный и существует (конечный или бесконечный) предел  . Тогда при l > 1 ряд (4.1) расходится, а при l < 1 сходится. При
. Тогда при l > 1 ряд (4.1) расходится, а при l < 1 сходится. При 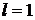 признак Даламбера не дает ответа о сходимости ряда.
признак Даламбера не дает ответа о сходимости ряда.
При 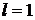 нужно использовать другой признак, чаще всего требуется применить предельный признак сравнения.
нужно использовать другой признак, чаще всего требуется применить предельный признак сравнения.
Доказательство. Рассмотрим вначале случай, когда l > 1.
Так как  , то при достаточно больших номерах
, то при достаточно больших номерах 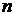 (например, для
(например, для  ) будет справедливо неравенство:
) будет справедливо неравенство:  или
или  , т.е. члены ряда возрастают с увеличением номера
, т.е. члены ряда возрастают с увеличением номера 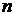 . По этой причине остаток ряда
. По этой причине остаток ряда  . Отсюда вытекает, что остаток ряда – расходится, и следовательно, по теореме 4.5 и сам ряд (4.1) расходится.
. Отсюда вытекает, что остаток ряда – расходится, и следовательно, по теореме 4.5 и сам ряд (4.1) расходится.
Пусть теперь l < 1. Возьмем какое-нибудь число q, удовлетворяющее неравенству l < q < 1 (например, положим  ). Тогда найдется такое натуральное число m, что при всех n > m будет выполняться неравенство:
). Тогда найдется такое натуральное число m, что при всех n > m будет выполняться неравенство:
 или
или  . Тогда
. Тогда

И остаток ряда
 – сходится (т.к. в скобках находится сумма бесконечно убывающей геометрической прогрессии). Отсюда вытекает, что ряд (4.1) сходится по теореме 4.5.
– сходится (т.к. в скобках находится сумма бесконечно убывающей геометрической прогрессии). Отсюда вытекает, что ряд (4.1) сходится по теореме 4.5.
Признак Даламбера применяют в следующих случаях:
1) в общий член ряда входит какое-нибудь число в степени, например,  ;
;
2) В общий член ряда входит факториал – последовательное произведение натуральных чисел:

 ,
,
 .
.
Пример 4.10. Исследовать на сходимость ряд 
Общий член ряда  содержит факториал и степени
содержит факториал и степени 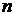 .
.
Применяем признак Даламбера.  .
.
Преобразуем отношение  .
.
Вычисляем предел 
Поэтому ряд сходится.