ТИПЫВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ
C позиций функционального анализа мы представили задачи в форме
прямой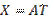 
или обратной 
, 
, 
.
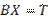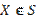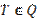Непосредственное вычисление ответа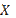 
возможно лишь в простых случаях. Обычно имеются трудности:
1. 
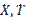принадлежат пространству континуальных функций, которые нельзя правильно представить ПК из-за дискретности представления чисел.
2. Оператор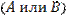 
– бесконечный ряд или неопределенный интеграл, вычислить который на ПК принципиально невозможно.
3. 
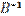неизвестно или вообще отсутствует.
4. Недопустимо возрастает погрешность округления непрерывных функций.
Основной принцип построения численных методов – так заменить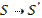 
, 
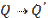и 
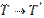, не изменяя 
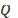, чтобы обеспечить непосредственное вычисление 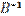и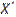 
, которое является аналогом .
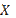Для качественной оценки образовавшейся погрешности – методической составляющей ошибки – надо 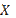и 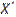рассмотреть в одном и том же пространстве.
Пример.
; 
; 
; 
.
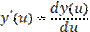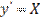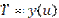Здесь 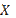и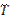 
– континуальные функции.
1) вариант: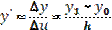 
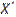, и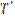 
- дискретные значения функций на сетке 
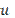с шагом 
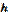. Для оценки 
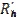мы отображаем 
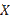на сетку .
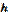2) вариант: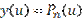 
, 
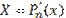, т.е. 
.
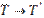Разработка конкретных способов замены элементов или пространства и оценка возникающей методической погрешности – основные проблемы численного анализа.
ТИПЫВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ
| МЕТОДЫПРЯМОГО ВЫЧИСЛЕНИЯ N заранее определено | МЕТОДЫПОСЛЕДОВАТЕЛЬНЫХ ПРРИБЛИЖЕНИЙ | |
| Приближение с переменным циклом | Итерационные процессы | Методы Монте-Карло |
Методы прямого вычисления
Применяется для решения некоторых прямых и даже обратных задач сразу или после замены задачей-аналогом.
Основные черты. Ход и количество операций вычислительного процесса (количество и тип элементарных операций) полностью определены заранее.
Примеры. Вычисление по явным формулам с рациональными алгебраическими соотношениями, решение СЛУ методом исключения неизвестных.
Вычисление радикальных, тригонометрических и трансцендентных функций в тех случаях, когда они трактуются как элементарные операции (здесь имеется методическая погрешность при вычислениях).
Ошибка отсутствует лишь в некоторых целочисленных задачах.
Методы последовательных приближений
Предусматривают построение бесконечных последовательносте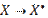й 
или 
для задачи-аналога.
Т.к. бесконечную последовательность обрывают на каком-то члене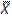 
, то методическая погрешность равна 
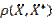или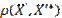 
.
Чтобы перейти от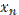 
к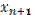 
нужна последовательность операций – цикл приближения.
В зависимости от способа (подхода) к построению циклов выделяют 3 основные группы процессов приближения:
1. С переменным циклом.
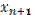может вычисляться независимо от , 
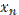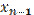, но содержание цикла меняется при росте номера N.
2. Итерационные.
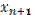вычисляется на основе 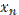, а иногда и нескольких предыдущих. В первом случае цикл остается неизменным от N.
3. На основе статистических испытаний (методы Монте-Карло).
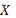– предел последовательности 
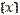оценок параметров построенной вероятностной модели.
Ценные свойства итерационных процессов и методов М-К – погрешности округления практически не накапливаются при построении новых членов .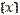
Для 1 группы погрешность определения возрастает при росте N. Это вызывает изменение цикла при изменении N. Центральный вопрос при реализации методов последовательных приближений - фиксация момента остановки.
Два подхода:
1. Заранее найти оценки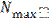 
путем детального исследования задачи.
2. В процессе приближений автоматически определить .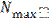
Выбор метода – на основе критериев (точность, время счета)