Лекция 2 Расчеты цилиндрических передач на прочность
Вопросы, рассматриваемые на лекции:
1. Силы, действующие в зацеплении;
2. Расчет зубьев по изгибной прочности;
3. Расчет зубьев по контактным напряжениям;
4. Проектный расчет;
5. Поверочный расчет;
Силы, действующие в зацеплении
Силы, действующие в зацеплении, определяются передаваемым вращающим моментом, размерами колес и формой зубьев.
Окружная сила P, определяется делительным диаметром и вращающим моментом: P = 2 T /dW.
Радиальная сила: PR =P tg αW
Нормальная сила, действующая по линии зацепления: Pn =P/ Cos αW.
 | |||
 | |||
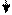 T1
T1
 | |||||
 | |||||
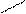 |














 P0 β P
P0 β P


|
 Pn PR Pn αW
Pn PR Pn αW
 |  | ||||
 | |||||
Рис. 1 Схема сил, действующих в зацеплении
В передачах с наклонными зубьями будет действовать дополнительная сила, представляющая собой проекцию нормальной силы на ось вращения колеса, и определяемая углом наклона зубьев: P0 = Pn Sin β. Аналогично будет определяться осевая сила в колесах с круговыми зубьями. В этом случае угол β представляет собой угол наклона касательной в точке зацепления к профилю зуба.
В процессе передачи вращения имеют место потери мощности, которые влияют на КПД зубчатой передачи:
η = η1 η2
где η1 - учитывает потери в зацеплении, η2 - учитывает потери в подшипниках.
В зависимости от типа подшипников, а также качества поверхности и точности изготовления зубчатых колес выбирают КПД передачи в диапазоне η = 0,97-0,99. КПД определяет соотношение мощностей на входном и выходном валах передачи: Nвых = Nвх η.
Расчет зубьев по изгибной прочности
В зубчатой передаче зубья перекатываются друг по другу и скользят. Поэтому они подвергаются следующим воздействиям: изгибу, контактным напряжениям, износу, заеданию.
Наибольшие изгибные напряжения возникают в момент входа зубьев в зацепление. Согласно схеме рис. 2 зуб подвергается изгибу от силы Pn’ и сжатию от силы Pn”.


 b1
b1


 Pn Pn’
Pn Pn’





 αw’
αw’
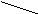
 Pn”
Pn”
 hn
hn
a0 a0




 b0
b0
 |  |

 a
a
Рис. 2 Схема действия сил на единичный зуб шестерни
На зубе можно выделить два участка – эвольвентный a0 b1, которым работает зуб, и циклоидный a0b0. Если вписать в зуб балку равного сопротивления, то сечение, в котором она касается контура зуба a0 a0, будет являться опасным.
Полное напряжение в зубе определяется суммой изгибных и сжимающих напряжений:
σ = σи ± σсж (1)
 ;
;  , (2)
, (2)
где b – ширина зуба, a – толщина зуба в опасном сечении, W – момент сопротивления, Mи – изгибающий момент.
После подстановки (2) в (1) получим:
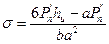 (3)
(3)
В этом выражении знак (-) применен по той причине, что большинство материалов работают на сжатие лучше, чем на растяжение. Хотя напряжение сжатия велико, за расчетное принимается напряжение растяжения.
Если выразить входящие в (3) силовые компоненты через реальную силу зацепления и угол зацепления и принять обозначения: hи=λ1m и a= λ2m, то выражение (3) перепишется в виде:
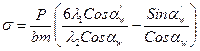 (4)
(4)
Выражение в круглых скобках представляет собой коэффициент прочности зуба YFH, который зависит от числа зубьев, их высотных пропорций, угла зацепления, коэффициентов коррекции. Значения этого коэффициента приводятся в справочниках в виде таблиц и графиков.
С учетом этого выражение (4) может быть представлено в виде:
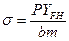
По этой формуле рассчитывают зубья тихоходных и редко работающих передач, когда число их циклов нагружения за срок службы значительно меньше базового. Большинство зубчатых передач работают интенсивно и их зубья рассчитывают на выносливость с учетом концентрации напряжений:
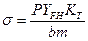 (5)
(5)
где КТ – эффективный коэффициент концентрации напряжений.
Приняв обозначение YF = YFH KT (коэффициент прочности зуба с учетом концентрации напряжений), получим:
 (6)
(6)
Для передач с зубчатыми колесами, имеющими число зубьев Z=16-100 – YFH=2,96-1,95 YF = 4,47-3,75. При этом наибольшие изгибные напряжения зубьев возникают у колес с меньшим их числом, поэтому расчет на изгиб зубьев проводится для шестерни.