Несобственные интегралы первого рода

Вычисление длины дуги плоской кривой

Пусть известна функция и требуется найти длину дуги, заданной функцией , где .

Для определения длины дуги необходимо вычислить определенный интеграл:

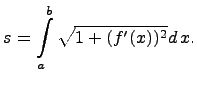
Рассмотрим случай параметрического задания кривой:

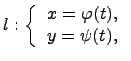
где . В этом случае для определения длина дуги вычисляется определенный интеграл:

Рассмотрим случай, когда кривая задается в полярных координатах где . Тогда для определения длины дуги вычисляется следующий определенный интеграл:

5.

Вычисление объемов с помощью тройных интегралов

Объем тела U в декартовых координатах Oxyz выражается формулой В цилиндрических координатах объем тела равен 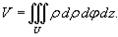В сферических координатах, соответственно, используется формула

Пример 1

Найти объем конуса высотой H и радиусом основания R (рисунок 2). Решение.     Рис.1     Конус ограничен поверхностью и плоскостью z = H (рисунок 1). В декартовых координатах его объем выражается формулой Вычислим этот интеграл в цилиндрических координатах, которые изменяются в пределах Получаем (не забудем включить в интеграл якобиан ρ): Находим объем конуса:

6.

Относительно подынтегральной функции мы будем предполагать, что она непрерывна на отрезке интегрирования, а также, когда это понадобится, что она имеет на этом отрезке производные до некоторого порядка.

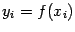Вычислять значение интеграла мы будем по значениям функции в некоторых точках отрезка . Эти значения мы будем предполагать известными, то есть предполагать, что у нас есть некоторый эффективный способ вычисления значений функции с любой требуемой точностью. Формулы, позволяющие по известным значениям приближённо определить значение , называются квадратурными формулами.

Для наглядности мы будем прибегать к геометрической интерпретации смысла определённого интеграла, как площади некоторой криволинейной трапеции, в случае функции . Следует, однако, иметь в виду, что квадратурные формулы, которые мы будем получать, имеют смысл для функций, принимающих значения произвольного знака.

При вычислить интеграл значит найти площадь под графиком , расположенную над отрезком . Естественной идеей является следующее построение: разобьём отрезок на части точками деления и положим и (см. определение значения определённого интеграла). Тогда разбиение отрезка состоит из отрезков при 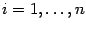. Вместо площади под графиком, равной , будем приближённо находить суммарную площадь узких полосок, лежащих над отрезками разбиения (см. рис.).

Рис.5.1.

Несобственные интегралы первого рода

Определение Предположим, что функция задана на бесконечном промежутке вида и интегрируема на любом конечном отрезке , где . Таким образом, можно рассмотреть функцию, зависящую от верхнего предела, как от переменной:

Если эта функция имеет предел при , то число 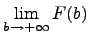называется значением несобственного интеграла первого рода:

а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения.