Содержание
Введение. 3
1 ПОСТАНОВКА ЗАДАЧИ.. 4
2 ПОСТРОЕНИЕ ВРЕМЕННОГО РЯДА.. 5
3 ОПРЕДЕЛЕНИЕ АВТОКОРРЕЛЯЦИИ И ПОСТРОЕНИЕ КОРРЕЛОГРАММЫ.. 6
4 ПОСТРОЕНИЯ ТРЕНДОВОЙ СОСТАВЛЯЮЩЕЙ ВРЕМЕННОГО РЯДА.. 7
5 ВЫДЕЛЕНИЕ ЦИКЛИЧЕСКОЙ И СЛУЧАЙНОЙ СОСТАВЛЯЮЩИХ ВРЕМЕННОГО РЯДА.. 9
6 ОПРЕДЕЛЕНИЕ СТРУКТУРНОЙ СТАБИЛЬНОСТИ ВРЕМЕННОГО РЯДА.. 14
Заключение. 18
Введение
Целью данной работы является проведение исследования одномерных временных рядов на основе исходных данных и при помощи средств Statistica 6.1.
Для достижения обозначенной цели необходимо решить ряд взаимосвязанных задач:
1) выполнить графическое отображение временного ряда и определить гипотезу о наличии компонент и виде временного ряда;
2) построить коррелограмму для l=n/2;
3) построить трендовую составляющую временного ряда по линейной, степенной моделям и по модели согласно выдвинутой гипотезе;
4) выбрать наилучший вид тренда;
5) выделить циклическую и случайную составляющую при аддитивной и мультипликативной моделях;
6) выполнить графическое отображение каждого вида компонент и во всей совокупности согласно модели по выдвинутой гипотезе;
7) определить структурную стабильность временного ряда.
Временные ряды представляют собой парные регрессии: y=f(t).
Самое широкое применение модели временных рядов нашли в исследовании финансовых рынков, в анализе динамики финансовых показателей, прогнозирование цен на различные товары, курсов акций, соотношение курсов валют и т.д.
ПОСТАНОВКА ЗАДАЧИ
По исходным данным таблицы 1.1 необходимо провести анализ временного ряда, характеризующего сведения о курсе австралийского доллара по отношению к российскому рублю.
| Дни | Цена, руб. | |
| 1.11.2007 | 11,0702 | |
| 2.11.2007 | 11,0951 | |
| 3.11.2007 | 11,0321 | |
| 4.11.2007 | 11,0143 | |
| 5.11.2007 | 10,9477 | |
| 6.11.2007 | 10,9458 | |
| 7.11.2007 | 10,9442 | |
| 8.11.2007 | 10,9802 | |
| 9.11.2007 | 11,0224 | |
| 10.11.2007 | 10,996 | |
| 11.11.2007 | 10,9895 | |
| 12.11.2007 | 10,9927 | |
| 13.11.2007 | 10,9609 | |
| 14.11.2007 | 10,9684 | |
| 15.11.2007 | 10,9333 | |
| 16.11.2007 | 10,9399 | |
| 17.11.2007 | 10,9513 | |
| 18.11.2007 | 10,927 | |
| 19.11.2007 | 10,9265 | |
| 20.11.2007 | 10,8908 | |
| 21.11.2007 | 10,8975 | |
| 22.11.2007 | 10,9462 | |
| 23.11.2007 | 10,9256 | |
| 24.11.2007 | 10,8922 | |
| 25.11.2007 | 10,9388 | |
| 26.11.2007 | 11,0155 | |
| 27.11.2007 | 11,0224 | |
| 28.11.2007 | 11,0105 | |
| 29.11.2007 | 11,0303 | |
| 30.11.2007 | 11,0323 |
Исходные данные для исследования представлены в таблице 1.1. Источник данных – официальный сайт газеты “Коммерсант”.
Таблица 1.1 – Исходные данные
ПОСТРОЕНИЕ ВРЕМЕННОГО РЯДА
На первом шаге исследования необходимо построить временной ряд. Графическое отображение временного ряда по исходным данным приведено на рисунке 2.1.

Рисунок 2.1 – Графическое отображение временного ряда
По графическому отображению временного ряда можно предположить, что временной ряд содержит две компоненты (тенденцию и случайную), которые соединяются по мультипликативной модели, цикл не просматривается.
ОПРЕДЕЛЕНИЕ АВТОКОРРЕЛЯЦИИ И ПОСТРОЕНИЕ КОРРЕЛОГРАММЫ
Проверка гипотезы о взаимосвязи компонент временного ряда осуществляется на основе изучения абсолютных коэффициентов автокорреляции. Следовательно, следующим шагом исследования является определение автокорреляции уровней ряда до n/2 и построение коррелограммы.
Для оценки автокорреляции рассматриваются коэффициенты парной корреляции различного порядка, и строится коррелограмма, имеющая стандартный вид (см. рисунок 3.1).
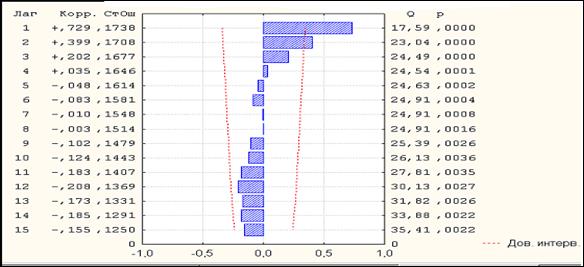
Рисунок 3.1 - Автокорреляционная функция для курса австралийского доллара по дням
Так как коэффициент автокорреляции первого порядка является наибольшим по абсолютному значению (0,729) и значимым, временной ряд содержит тенденцию и случайную компоненту.
ПОСТРОЕНИЯ ТРЕНДОВОЙ СОСТАВЛЯЮЩЕЙ ВРЕМЕННОГО РЯДА
Далее необходимо построить трендовую составляющую временного ряда по линейной и степенной моделям, учитывая, что тренд временного ряда есть парная зависимость, в которой в качестве фактора выступает временной показатель (см. рисунок 4.1 и рисунок 4.2). Уравнение линейного и степенного трендов соответственно имеют вид:



Рисунок 4.1 – Вид временного ряда при наличии линейного тренда
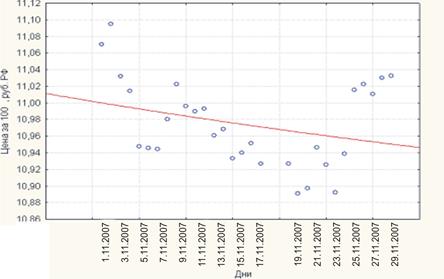
Рисунок 4.2 - Вид временного ряда при наличии степенного тренда
Затем выполняем оценку трендов на основе средней относительной ошибки аппроксимации (см. рисунок 4.3)

Рисунок 4.3 – Вид диалогового окна с исходными данными после расчета
средней относительной аппроксимации по линейному и степенному тренду
Так как величина погрешности (Yt-Yt(теор.)) не является довольно существенной, то можно использовать модель временного ряда, используя только трендовую составляющую.