В жизни при протекании реальных экономических процессов может происходить резкое изменение внешних условий. В этом случае временные ряды изменяют свою тенденцию. Наличие единой тенденции во всем периоде исследования называется структурной стабильностью временного ряда. При наличии нескольких тенденций структурная стабильность нарушается.
В качестве моделей для таких рядов используются кусочные функции линейного и нелинейного вида. Кусочно-линейная регрессия с точками разрыва для зависимой переменной – стоимостью австралийского доллара приведена на рисунке 6.1.

Рисунок 6.1 – Вид фрагмента таблицы с результатами оценки кусочно-линейной функции
Кусочно-линейная регрессия, отражающая зависимость курса австралийского доллара от различных экономических факторов, может быть записана двумя способами.
1). С помощью системы уравнений:

2). С помощью фиктивных переменных, которые определяют переход по отрезкам времени.

Для построения на одной диаграмме исходных и предсказанных значений в таблицу исходных данных следует добавить новую переменную d, для которой значения вычисляются по формуле 6.1.
 (6.1)
(6.1)

Рисунок 6.2 – Вид рабочего листа со значениями кусочно-линейной функции
Графическое отображение приведено на рисунке 6.3.

Рисунок 6.3 – Диаграмма курса австралийского доллара по исходным данным
и кусочно-линейной функции
Выдвигаем гипотезу о том, что ряд является структурно – стабильным. Доказательство проводится на основании критерия Грегори Чоу (рассчитывается F-статистика, показывающая отношение разности суммы квадратов остатков по кусочной модели и по единой регрессии к остаточным суммам квадратов по кусочной модели). Значения рассчитанных величин для критерия Грегори Чоу приведены на рисунке 6.4.

Рисунок 6.4 – Рассчитанные величины для критерия Грегори Чоу
Значения параметров для расчета F – статистики приведены в таблице 6.1.
Таблица 6.1 – Данные для теста Чоу
| № | Вид уравнения | Число наблюдений | Остаточная сумма квадратов | Число параметров в уравнении | Число степеней свободы остаточной дисперсии |
| Кусочно-линейная модель | |||||
| (1) | y(1)=11,114719-0,001820×t | 0,0094 | |||
| (2) | y(2)=11,080221-0,00059×t | 0,0081 | |||
| Уравнение тренда по всей совокупности | |||||
| (3) | y(3)= 11,1448-0,0015×t | 0,0733 |
Далее в соответствии с предложенной Г. Чоу методикой определяется фактическое значение F-критерия по следующим дисперсиям на одну степень свободы вариации:
Найденное значение F-статистики сравнивают с табличным, полученным по таблицам распределения Фишера для уровня значимости a и числом степеней свободы числителя и знаменателя.
По данным рисунку 6.4 определяем значения F – статистики:
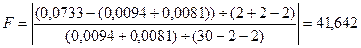
Табличное значение F(5%, 2, 26) = 3,37.
Fфакт. = 41,642 > Fтабл. = 3,37, следовательно гипотеза о структурной стабильности тенденции отклоняется, а влияние структурных изменений на динамику изучаемого показателя признают значимым; моделирование тенденции временного ряда следует осуществлять с помощью кусочно-линейной модели.
Заключение
В рамках данной работы была изучена такая область эконометрики, как одномерные временные ряды. Для этого был решён комплекс задач и получены следующие результаты:
1). На основании расчётов коэффициентов автокорреляции было выяснено, что временной ряд имеет тенденцию и случайную компоненту, так как наибольшим по высоте и значимым столбцом оказался первый.
2). Трендовая составляющая надежная, так как средние относительные ошибки аппроксимации, соответственно равные 4,06% и 1,4%. Величина погрешности не является довольно существенной, следовательно, использовать модель временного ряда, используя только трендовую составляющую допустимо.
3). Моделирование тенденции временного ряда следует осуществлять с помощью кусочно-линейной модели (не выполнен критерий Чоу):

4). При исследовании курса австралийского доллара по дням были построены:
1) линейный тренд:  ;
;
2) степенной тренд: 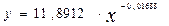 ;
;
3) аддитивная модель: Y=T+S+E, в которой Y=11,4213-0,0198×t; S1=0,000230; S2=0,013310;
S3=-0,00163;S4=0,003578; S5=-0,016954;E2=0,005826.
4) мультипликативная модель: Y=T×S×E, которой Y=11,2998-0,0127×t; S1=99,9338; S2=100,1544;
S3=100,0028; S4=100,0899; S5=99,8191; E2=29,999326.
5) структурная модель:

5). При оценке моделей выяснилось, что линейный тренд предпочтительнее степенного тренда и кусочно-линейной модели. В свою очередь аддитивная модель предпочтительнее, чем мультипликативная модель.