Адсорбция
Понятие адсорбции. Автоадсорбция. Адсорбент и адсорбат. Абсолютная и Гиббсовская адсорбция. Единицы измерения адсорбции. Зависимость величины адсорбции от концентрации, давления и температуры. Изотерма, изобара, изопикна, изостера адсорбции
Адсорбция - процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.
Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры - уплотнение, которое называется автоадсорбцией.
В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.
Вещество, на поверхности которого происходит адсорбция, называется адсорбентом, а вещество, которое перераспределяется – адсорбатом.
Обратный процесс перехода вещества с поверхности в объем фазы - десорбция.
В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость - жидкость, жидкость - газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:
А = m1/m2 - абсолютная адсорбция, А = ni/S.
Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).
Адсорбция зависит от концентрации компонентов и температуры.
А = f(c,T) - жидкость;
А = f(P,T) - газ
Различают следующие виды зависимостей:
| 1. Изотерма (рис. 8) | 2. Изобара | 3. Изостера |
| А=fT(c) | А=fP(T) | c=fA(T) |
| A=fT(P) | A=fC(T) | P=fA(T) |
Фундаментальное уравнение Гиббса. Определение Гиббсовской адсорбции. Адсорбционное уравнение Гиббса
Считаем V поверхности раздела = 0.
dU = TdS +s dS+ 
Проинтегрировав, получим: U = TS + sS+
Полный дифференциал от этого уравнения:
dU = TdS + SdT + sdS + 
+ Sds + 
.
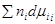Подставляя значение dU из (6) в (7) и сократив одинаковые члены правой и левой части, получим:
SdT + Sds + 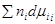= 0.
Предположим, что T = const: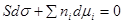 
Разделив правую и левую часть на поверхность S, получим фундаментальное адсорбционное уравнение Гиббса:
; 
;
.
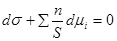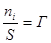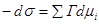Определение зависимости поверхностного натяжения от адсорбции одного компонента, при постоянстве химических потенциалов других компонентов.
.
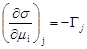Известно, что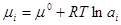 
, 
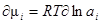, (где 
, 
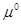- равновесный и стандартный химический потенциал компонента i; ln ai - логарифм активности i –го компонента). Тогда уравнение Гиббса будет выглядеть так
Активность связана с концентрацией: с = ×а. Предположим, что = 1 (при с ® 0). Тогда
- для жидкости и газа
Обычно уравнение Гиббса применяют для растворов. Растворителем может быть не только индивидуальное вещество, но и смесь. В разбавленных растворах гиббсовская адсорбция очень мала, а его химический потенциал меняется очень мало с изменением концентрации растворенного вещества, т.е. d m= 0. Поэтому для разбавленного раствора фундаментальное уравнение Гиббса выглядит так:
Из этих уравнений следует, что зная зависимость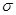 
= f(С) (где С - концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных 
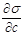в этих точках.
Зная эти производныеуравнения Гиббса, можно рассчитатьзначение Г, что позволяет построить зависимость Г = f(С). Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R. Так как величина R отнесена к молю вещества, а s- к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м2], то R нужно подставлять: R= 8,314 Дж/моль×К.