Из формулы для ускорений следует, что если движущаяся система отсчета
движется относительно первой без ускорения, то есть  , то
, то
ускорение  тела относительно обеих систем отсчета одинаково.
тела относительно обеих систем отсчета одинаково.
Поскольку в Ньютоновской динамике из кинематических величин именно
ускорение играет роль, то, если довольно естественно предположить, что
силы зависят лишь от относительного положения и скоростей физических
тел (а не их положения относительно абстрактного начала отсчета), окажется,
что все уравнения механики запишутся одинаково в любой инерциальной
системе отсчета — иначе говоря, законы механики не зависят от того, в какой
из инерциальных систем отсчета мы их исследуем, не зависят от выбора в
качестве рабочей какой-либо конкретной из инерциальных систем отсчета.
Также — поэтому — не зависит от такого выбора системы отсчета
наблюдаемое движение тел (учитывая, конечно, начальные скорости). Это
утверждение известно как принцип относительности Галилея, в отличие от
Принципа относительности Эйнштейна
14. Движение тела в поле силы тяжести. Свободное падение. Движение тела под действием нескольких сил. Равнодействующая. Одним из проявлений силы всемирного тяготения является сила тяжести.
Сила тяжести - сила, действующая на любое материальное тело, находящееся вблизи поверхности Земли или другого астрономического тела.

Любое тело, находящееся на Земле (или вблизи нее), вместе с Землей вращается вокруг ее оси, т.е. тело движется по окружности радиусом r с постоянной по модулю скоростью.
На тело на поверхности Земли действуют сила тяготения  и сила со стороны земной поверхности
и сила со стороны земной поверхности 
Их равнодействующая

сообщает телу центростремительное ускорение

Разложим силу тяготения на две составляющие, одна из которых будет, т.е.

Из уравнений (1) и (2) видим, что
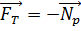
Таким образом, сила тяжести 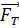 - одна из составляющих силы
- одна из составляющих силы
тяготения, вторая составляющая 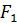 сообщает телу центростремительное ускорение.
сообщает телу центростремительное ускорение.
В точке М на географической широте 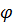 сила тяжести направлена не по радиусу Земли, а под некоторым углом
сила тяжести направлена не по радиусу Земли, а под некоторым углом 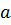 к нему.
к нему.
Сила тяжести направлена по, так называемой, отвесной прямой (по вертикали вниз).
Сила тяжести равна по модулю и направлению силе тяготения только на полюсах. На экваторе они совпадают по направлению, а по модулю отличие наибольшее.

где  — угловая скорость вращения Земли, R — радиус Земли.
— угловая скорость вращения Земли, R — радиус Земли.


Так как  очень мала, то
очень мала, то 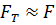 . Следовательно, сила тяжести мало
. Следовательно, сила тяжести мало
отличается по модулю от силы тяготения, поэтому данным различием часто
можно пренебречь.

Из этой формулы видно, что ускорение свободного падения g не зависит от массы падающего тела, но зависит от высоты.
Если М - масса Земли,  - радиус земли, m - масса данного тела, то сила тяжести равна
- радиус земли, m - масса данного тела, то сила тяжести равна
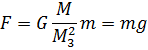
где g - ускорение свободного падения у поверхности Земли:

Сила тяжести направлена к центру Земли. В отсутствие других сил тело свободно падает на Землю
с ускорением свободного падения.
Если на тело действует только сила тяжести, то тело совершает свободное падение. Вид траектории движения зависит от направления и модуля начальной скорости. При этом возможны следующие случаи движения тела:
1. Если начальная скорость тела направлена под углом к силе тяжести, то тело будет двигаться по параболе,
либо по ветви параболы.
2. Тело может двигаться по круговой или эллиптической орбите вокруг планеты Земля.
3. Если начальная скорость тела равна нулю или параллельна силе тяжести, тело совершает прямолинейное
свободное падение.
Свободное падение тел - это падение тел на Землю в вакууме при отсутствии помех.
Движение тела под действием силы тяжести при отсутствии сопротивления воздуха можно считать свободным падением. Например, в свободном падении находится спортсмен, прыгающий в воду с вышки или мяч, выпущенный из руки.
В1583 году итальянский учёный Галилео Галилей (1564-1642) установил, что при отсутствии сопротивления воздуха все тела, независимо от их массы, падают на землю с одинаковым ускорением g, которое направлено вертикально вниз. Это ускорение
называется ускорение свободного падения. При свободном падении тела с небольшой высоты h от поверхности Земли (причём h намного меньше радиуса Земли R3, где радиус Земли R3 ~ 6000 км) сила притяжения остаётся практически постоянной,
поэтому ускорение свободного падения также остаётся постоянным.
Это заключение подтверждает опыт с падением тел в стеклянной трубке, из которой выкачан воздух (рис. 1.24). Кусочек свинца, лёгкое пёрышко и дробинка достигают дна трубки одновременно. Следовательно, они падают с одинаковым ускорением.
Свободное падение можно рассматривать как частный случай равноускоренного движения. Ускорение свободного падения зависит от высоты над уровнем моря и от географической широты места. Оно изменяется примерно от 9,83 м/с2 на полюсе и до
9,78 м/с2 на экваторе. На широте Москвы ускорение свободного падения принимается равным g = 9,8 м/с2. Поэтому в большинстве случаев при решении задач по физике ускорение свободного падения принимается равным 9,8 м/с2.
Движение тела под действием нескольких сил второй закон Ньютона:
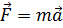
где F - это векторная сумма всех сил, приложенных к телу.
Векторное сложение сил можно заменить их алгебраическим сложением их проекций на координатные оси. При решении задач по механике, необходимо сначала изобразить на чертеже векторы всех сил, действующих не тело, и ускорения тела
(если известно его направление). После выбора направления координатных осей, необходимо найти проекции всех векторов на эти оси. Далее нужно составить уравнение второго закона Ньютона для проекций на каждую ось и решить полученные скалярные уравнения.
28. Момент силы и момент импульса относительно точки.
Уравнение моментов для материальной точки. Момент силы и момент
импульса абсолютно твердого тела относительно оси вращения.
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Если имеется материальная точка  , к которой приложена сила
, к которой приложена сила  , то момент силы относительно точки О равен векторному произведению радиус-вектора
, то момент силы относительно точки О равен векторному произведению радиус-вектора 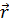 , соединяющего точки О и
, соединяющего точки О и 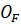 , на вектор силы
, на вектор силы  :
:
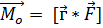
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную
оси, относительно точки пересечения оси с этой плоскостью.
Момент силы измеряется в ньютон-метрах. 1 Н*м — момент силы, который производит сила 1 Н на
рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент
количества движения) характеризует количество вращательного движения. Величина, зависящая от
того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью
происходит вращение.
Момент импульса L материальной точки относительно некоторого начала отсчёта определяется
векторным произведением её радиус-вектора и импульса: 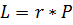 , где г — радиус-вектор частицы
, где г — радиус-вектор частицы
относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, Р — импульс
частицы.
где 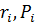 — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой
определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно
распределенной массой или вообще распределенной системы это может быть записано как

Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где dp— импульс бесконечно малого точечного элемента системы).
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж*c.
Вариант 23
103) уравнение движения точки по прямой:  м/c и В=0,125 м/
м/c и В=0,125 м/ 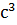 .
.
Определить силу, действующую на точку в момент времени t=1 c. Масса точки m=0,1 кг.
Дано

 m/с
B=0,125 m/ m/с
B=0,125 m/ 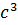 t=1 c
m=0,1 кг
F=?
t=1 c
m=0,1 кг
F=?
| Сила равна F=m*a
Необходимо найти ускорение а в момент t.
 Следовательно:
Следовательно:
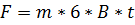
 Ответ: F=0,075 H
Ответ: F=0,075 H
|
117) Ледяная гора составляет с горизонтом угол  . Из некоторой точки по ней снизу вверх движется тело с начальной скоростью 10 м/с. Коэффициент трения скольжения 0,1. Определить скорость тела при его возвращении в ту же точку.
. Из некоторой точки по ней снизу вверх движется тело с начальной скоростью 10 м/с. Коэффициент трения скольжения 0,1. Определить скорость тела при его возвращении в ту же точку.
Дано:
α= 
 m/c m/c

| При движении вверх скорость уменьшается до нуля в верхней точке, предмет движется равнозамедленно,
прямолинейно. При движении вниз начальная скорость равна нулю, предмет движется равноускоренно.
Путь пройденный предметом, в обоих случаях одинаков и выражаемся:
 (1)
Приравняв правые части, получим: (1)
Приравняв правые части, получим:  (2)
Изобразим все силы, действующие на предмет, в обоих случаях.
Свяжем систему отсчета для обоих случаев движения: ось (2)
Изобразим все силы, действующие на предмет, в обоих случаях.
Свяжем систему отсчета для обоих случаев движения: ось 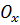 проложим вдоль ускорения, ось проложим вдоль ускорения, ось  – перпендикулярно к ней.
Второй закон Ньтона для движения вверх: – перпендикулярно к ней.
Второй закон Ньтона для движения вверх:  Проекции на оси:
Проекции на оси:
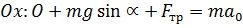 (3) (3)
 (4)
При больших скоростях сила трения скольжения прямо пропорциональна силе, прижимающей предмет к поверхности; эта сила по третьему закону Ньютона численно равна силе реакции опоры: (4)
При больших скоростях сила трения скольжения прямо пропорциональна силе, прижимающей предмет к поверхности; эта сила по третьему закону Ньютона численно равна силе реакции опоры:
 (5)Выразив N из (4) и подставив в (3) с учетом формулы (5), получим: (5)Выразив N из (4) и подставив в (3) с учетом формулы (5), получим:
 (6)
Запишем второй закон Ньютона для движения вниз: (6)
Запишем второй закон Ньютона для движения вниз:
 Проекции на оси:
Проекции на оси: 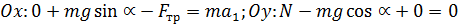 После преобразований, получим:
После преобразований, получим:
 . Выразив . Выразив 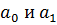 из (6) и (7), имеет: из (6) и (7), имеет:
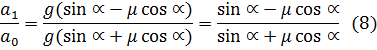 Подставив (8) в (2), получим:
Подставив (8) в (2), получим:
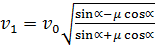 Подставим значения Подставим значения  м/с
Ответ: м/с
Ответ: 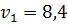 м/с м/с
|
121) Определить импульс силы полученный стенкой при ударе о нее шарика массой 300г, если шарик двигался со скоростью
8 м/с под углом  r к плоскости стенки. Удар о стенку считать упругим.
r к плоскости стенки. Удар о стенку считать упругим.
Дано:
m=300г
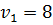 м/с
a= м/с
a= 

| Из интегральной формы второго закона Ньютона получаем, что изменение импульса шарика равно импульсу силы, который передал стенке:
 где
где  Так как удар абсолютно упругий, то скорости
Так как удар абсолютно упругий, то скорости 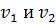 направлены в противоположные стороны и их модули равны друг другу. Тогда из уравнения направлены в противоположные стороны и их модули равны друг другу. Тогда из уравнения  получаем получаем 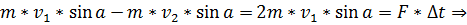
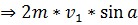 Подставляем числа
Подставляем числа
 м/с м/с 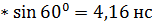 Ответ:
Ответ: 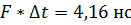 . .
|
131) Парашютист массой 70 кг совершает затяжной прыжок и через 14 с имеет скорость 60 м/с. Считая движение парашютиста равноускоренным, найти работу по определению сопротивления воздуха.
Дано
m=70кг
v=60м/с
t=14c
g=9,8 м/  A=?
A=?
| Так как движение равноускоренное, то скорость будет через время t равна v=a*t. Откуда ускорение равно:
 Парашютист пройдет путь
Парашютист пройдет путь 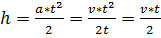 Поэтому изменение потенциальной энергии равно
Поэтому изменение потенциальной энергии равно 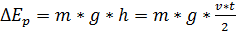 Изменение кинетической энергии равно
Изменение кинетической энергии равно 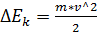 По закону сохранения работа по преодолению сопротивления воздуха равна разности изменений потенциальной и кинетической энергии:
По закону сохранения работа по преодолению сопротивления воздуха равна разности изменений потенциальной и кинетической энергии:
 Подставляем числовые значения:
Подставляем числовые значения:
 Ответ: А=162414 Дж.
Ответ: А=162414 Дж.
|
145) Маховое колесо, имеющее момент инерции 145 2 кг ×м, вращается, делая 10 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 1) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Дано
J=145 
 об/с
t=1 мин=60с
Мтр=?
N=? об/с
t=1 мин=60с
Мтр=?
N=?
| Уравнение движения 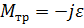 Угловое ускорение
Угловое ускорение


 Угол поворота
Угол поворота
 Число оборотов
Число оборотов 
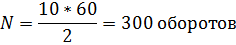 Ответ: Мтр=151,77 Н*м, N=300 оборотов.
Ответ: Мтр=151,77 Н*м, N=300 оборотов.
|
151) На обод маховика диаметром 60 см намотан шнур, к концу которого привязан груз массой 1 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно, за время 3 с приобрел угловую скорость 9 рад/с.
Дано
V1=10  V2=8
V2=8  m=70 кг
М=?
m=70 кг
М=?
| По закону сохранения момента импульса:
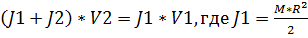 – момент инерции сплошного диска радиусом R и массой М,
V2 – начальная частота вращения человека с диском, J1+J2 – суммарный момент инерции диска и человека,
находящегося на краю диска, V1 – частота вращения после перехода человека в центр. Момент инерции человека J2=m*R2, так ка он стоял на расстоянии R от оси вращения.
Тогда – момент инерции сплошного диска радиусом R и массой М,
V2 – начальная частота вращения человека с диском, J1+J2 – суммарный момент инерции диска и человека,
находящегося на краю диска, V1 – частота вращения после перехода человека в центр. Момент инерции человека J2=m*R2, так ка он стоял на расстоянии R от оси вращения.
Тогда  Подставляем числа:
Подставляем числа: 
|
Вариант 16.
1) Уравнения движения материальной точки имеют вид 
где A,B,C,D,E –коэффициенты, которые задаются для каждого варианта.
Время 
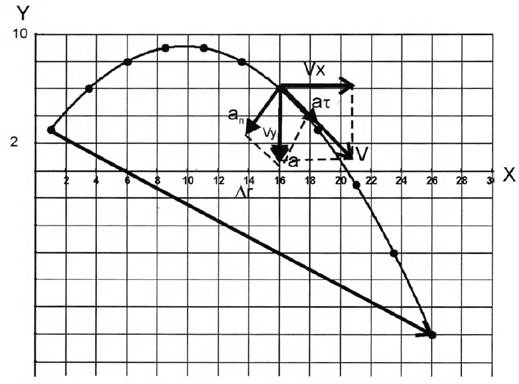
1) Построить траекторию в координатах XY. Для построения траектории необходимо определить значения X и Y из уравнений движения в интервале времени от 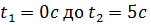 и полученные результаты внести в таблицу.
и полученные результаты внести в таблицу.
2) Определить аналитически перемещение ∆r в интервале времени  и указать на графике траектории.
и указать на графике траектории.
3) Определить величину мгновенной скорости V в заданный момент времени t и обозначить ее направление в произвольном масштабе.
4) Определить величину полного ускорения а в заданный момент времени t и обозначить его направление на графике в произвольном масштабе.
5) Определить величину тангенциального  ускорения в заданный момент времени t и обозначить их направления на графике в произвольном масштабе.
ускорения в заданный момент времени t и обозначить их направления на графике в произвольном масштабе.
Уравнения движения 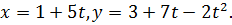 Составляем таблицу.
Составляем таблицу.
| t, c | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 | ||||||
| x | 3.5 | 8.5 | 13.5 | 18.5 | 23.5 | ||||||
| y | -1 | -6 | -12 |
Перемещение будет равно по закону Пифагора.
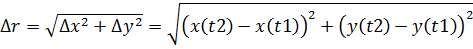


Строим вектор перемещения из точки 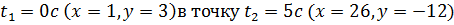
Скорость по определению 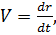 поэтому для проекции имеем:
поэтому для проекции имеем:
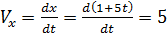 m/c,
m/c,  m/c.
m/c.
В момент времени t=3c имеем  м/с,
м/с,  м/с. Модуль скорости найдем по закону Пифагора:
м/с. Модуль скорости найдем по закону Пифагора:
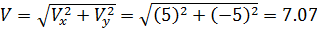 м/с.
м/с.
Строим в точке  скорость с проекциями
скорость с проекциями  м/с,
м/с,  м/с и сам вектор V, являющийся суммой векторов
м/с и сам вектор V, являющийся суммой векторов 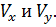
Ускорение по определению 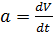 , поэтому для проекций имеем:
, поэтому для проекций имеем:
 м/с,
м/с,  . Строим в точке t=3c (x=16, y=6)
. Строим в точке t=3c (x=16, y=6)
ускорение а (учитываем что  =0)
=0)
Тангенциальное ускорение 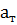 равно проекции полного ускорения а на вектор скорости V. Нормальное ускорение –
равно проекции полного ускорения а на вектор скорости V. Нормальное ускорение –
это проекция полного ускорения а на нормаль к скорости V. Получаем из подобия треугольников 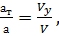 откуда
откуда
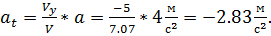 По правилу Пифагора
По правилу Пифагора 
2) Уравнение вращательного движения имеют вид: 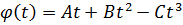 , где коэффициенты A,B,C задаются для каждого варианта. Время
, где коэффициенты A,B,C задаются для каждого варианта. Время 
1) Построить график 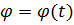 в интервале времени от
в интервале времени от 
2) Определить аналитически угловую скорость 
3) Построить график  в интервале времени от
в интервале времени от 
4) Определить аналитически угловое ускорение 
5) Построить график  в интервале времени
в интервале времени 

| t,c | 3,5 | ||||
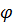 , рад , рад
| 7,2 | 16,6 | 17,4 | 11,2 |
Строим график:

Угловая скорость равна по определению: 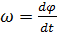 , поэтому
, поэтому  .
.
| t, c | 3,5 | ||||
 , рад/с , рад/с
| 2,5 | 10,1 | 6,9 | -7,1 | -18,15 |

Угловое ускорение равно по определению: 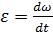 , поэтому
, поэтому 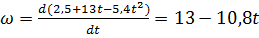 .
.
| t, c | 3,5 | ||||
 , рад/ , рад/ 
| 2,2 | -8,6 | -19,4 | -24,8 |
Строим график:

3) На материальную точку массой m действуют две консервативные силы  направленные под углом α друг к другу.
направленные под углом α друг к другу.
4) Начальная скорость 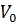 точки направлена по результирующей силе. Числовые значения массы, сил, начальной скорости и угла между силами для каждого варианта приведены в таблице ниже. Время
точки направлена по результирующей силе. Числовые значения массы, сил, начальной скорости и угла между силами для каждого варианта приведены в таблице ниже. Время  Определить
Определить
1) Ускорение а материальной точки
2) Скорость и координаты материальной точки в заданные моменты времени 
3) Величину импульса материальной точки р в моменты  . Проверить выполнение основного закона динамики.
. Проверить выполнение основного закона динамики.
4) Работу А результирующей силы в интервале времени  по теореме о кинетической энергии.
по теореме о кинетической энергии.
5) Величину кинетической энергии материальной точки в момент времени 
6) Работу А результирующей силы в заданном интервале времени  по теореме о кинетической энергии
по теореме о кинетической энергии
7) Величину потенциальной энергии  в момент времени
в момент времени  , приняв начальную потенциальную энергию
, приняв начальную потенциальную энергию 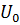 при
при 
равной нулю.
8) Механическую энергию материальной точки в моменты времени  . Проверить выполнение закона сохранения механической энергии.
. Проверить выполнение закона сохранения механической энергии.

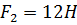
 м/с
м=4 кг м/с
м=4 кг
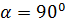
| Суммарная сила равна по теореме косинусов 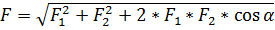 , где , где 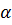 угол между силами
угол между силами  . Подставляем числа: . Подставляем числа:
 По второму закону Ньютона F=m*a, поэтому ускорение
По второму закону Ньютона F=m*a, поэтому ускорение  м/ м/  Скорость изменяется по закону
Скорость изменяется по закону 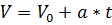 . В момент времени . В момент времени 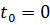 скорость скорость  м/с.
В момент времени м/с.
В момент времени  скорость скорость  м/с
Координата в начальный момент времени м/с
Координата в начальный момент времени  , тогда координата в момент времени , тогда координата в момент времени  будет равна будет равна  Импульсы будут равны
Импульсы будут равны 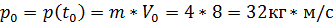 и и  Из основного закона динамики
Из основного закона динамики  . Изменение импульса за время . Изменение импульса за время 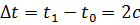 равно
равно  кг*м/с.
Тогда кг*м/с.
Тогда 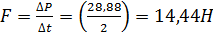 . Видно, что это значение с точностью 0,02Н (это наша погрешность вычислений) равно суммарной силе действующей на тело. Поэтому основной закон динамики выполняется.
Работа А результирующей силы F равна . Видно, что это значение с точностью 0,02Н (это наша погрешность вычислений) равно суммарной силе действующей на тело. Поэтому основной закон динамики выполняется.
Работа А результирующей силы F равна 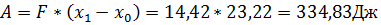
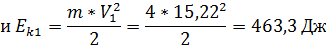 Работа по теореме о кинетических энергиях равна
Работа по теореме о кинетических энергиях равна  .
Из закона сохранения энергии .
Из закона сохранения энергии 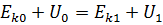 имеем потенциальную энергию имеем потенциальную энергию  .
Так как .
Так как 
|
Механическая энергия в 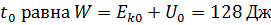
Механическая энергия в 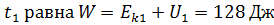
4. В шар массой m2, висящий на жестком стержне, попадает снаряд массой ml.
1) Определить кинетическую энергию шара со снарядом 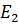 , если скорость снаряда
, если скорость снаряда
столкновения V1.
2) Высоту, на которую поднимется шар со снарядом
3) Определить часть кинетической энергии снаряда, перешедший во внутреннюю.


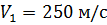
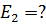 H=?
H=?
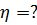
|
Импульс пули равен  . После столкновения суммарный импульс шара и снаряда должен быть равен, по закону сохранения импульса, импульсу снаряда: . После столкновения суммарный импульс шара и снаряда должен быть равен, по закону сохранения импульса, импульсу снаряда:  , где , где  - общая скорость снаряда и шара после столкновения.
Откуда - общая скорость снаряда и шара после столкновения.
Откуда  . Тогда начальная кинетическая энергия шара и снаряда равна . Тогда начальная кинетическая энергия шара и снаряда равна
 Подставляем числа:
Подставляем числа:  Через время кинетическая энергия перешла в изменение потенциальной энергии закону сохранения энергии:
Через время кинетическая энергия перешла в изменение потенциальной энергии закону сохранения энергии:  Поэтому
Поэтому  откуда откуда  Подставляем числа:
Подставляем числа:  Начальная кинетическая энергия пули была равна
Начальная кинетическая энергия пули была равна 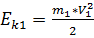 Энергия которая была затрачена на деформацию равна разности
Энергия которая была затрачена на деформацию равна разности  Доля этой энергии равна
Доля этой энергии равна  Подставляем числа:
Подставляем числа: 
|
5) Шар, движущийся со скоростью 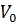 , столкнулся с покоящимся шаром такой же массы (удар нецентральный). Первый шар отлетел на угол, составляющий он с первоначальным направлением движения, второй - на угол
, столкнулся с покоящимся шаром такой же массы (удар нецентральный). Первый шар отлетел на угол, составляющий он с первоначальным направлением движения, второй - на угол  . Найти скорость первого шара после удара.
. Найти скорость первого шара после удара.




| Из закона сохранения импульса находим:  . Разложим вектора импульсов на проекции вдоль осей X и Y:
Вдоль оси X: . Разложим вектора импульсов на проекции вдоль осей X и Y:
Вдоль оси X:  Вдоль оси Y: Вдоль оси Y:  Из второго уравнения находим скорость
Из второго уравнения находим скорость  .-------------------------------------------------------
Подставляем в первое уравнение .-------------------------------------------------------
Подставляем в первое уравнение 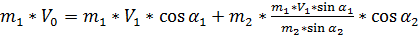 Откуда скорость
Откуда скорость  Так как
Так как 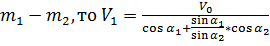 Подставляем числа
Подставляем числа 
|
6) На тело, имеющее момент инерции J, действуют две касательные  . При этом
. При этом
 - плечо первой силы,
- плечо первой силы,  - второй. Начальная угловая скорость тела
- второй. Начальная угловая скорость тела  . Числовые
. Числовые
значения момента инерции I, сил, начальной скорости задаются для каждого варианта. Время  .
.
Определить:
1) величину и направление результирующего момента сил
2) угловое ускорение 
3) угловую скорость 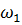 и угол поворота
и угол поворота  в заданный момент времени
в заданный момент времени 
4) Величину момента импульса L в моменты времени t0 и 
5) работу А результирующего момента сил в заданном интервале времени  по формуле механической работы
по формуле механической работы
6) величину кинетической энергии вращения 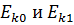 в моменты времени to и
в моменты времени to и 
7) работу А результирующей силы в заданном интервале времени  по теореме о кинетической энергии
по теореме о кинетической энергии


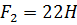

| Момент сил будет равен 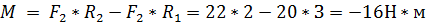 . Так как момент сил получился отрицательным, то вращение происходит против часовой стрелки и момент сил перпендикулярен плоскости рисунка и направлен на нас.
По определению момент сил равен . Так как момент сил получился отрицательным, то вращение происходит против часовой стрелки и момент сил перпендикулярен плоскости рисунка и направлен на нас.
По определению момент сил равен  - момент инерции тела, - момент инерции тела,  – угловое ускорение.
Откуда – угловое ускорение.
Откуда  Так как у нас вращение равноускоренное, то угловая скорость изменяется со временем по закону:
Так как у нас вращение равноускоренное, то угловая скорость изменяется со временем по закону: 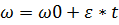 , где , где  - начальная угловая скорость.
Подставляем числа. - начальная угловая скорость.
Подставляем числа.  = 11рад/с + 0,889рад/с *2с = 12.778рад/с.
Угол поворота равен = 11рад/с + 0,889рад/с *2с = 12.778рад/с.
Угол поворота равен 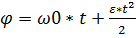 .
Подставляем числа .
Подставляем числа  Моменты импульса равно
Моменты импульса равно 
 Работа равна по определению
Работа равна по определению  По определению кинетическая энергия вращательного движения равна
По определению кинетическая энергия вращательного движения равна 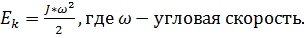 Поэтому
Поэтому 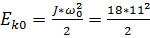 =1089Дж =1089Дж
 Работа А результирующей силы в заданном интервале времени
Работа А результирующей силы в заданном интервале времени  по теореме кинетической энергии равна по теореме кинетической энергии равна  Дж (она равна точностью 0,02Дж - точностью вычислений, работе вычисленной по другой формуле) Дж (она равна точностью 0,02Дж - точностью вычислений, работе вычисленной по другой формуле)
|