Проблема теплоемкости электронов проводимости на раннем этапе развития теории металлов оказалась непреодолимо трудной. Согласно классической статистической механике на каждую степень свободы частицы должна приходиться энергия, равная 
. На свободную частицу приходится теплоемкость, равная 
. В металлах ионы образуют решетку, погруженную в электронный газ свободных электронов, концентрация которых примерно такая же, как и число атомов. Поэтому теплоемкость металлов должна складываться из теплоемкости решетки 
и теплоемкости электронного газа 
:
. (2.26)
Если бы электронный газ был обычным классическим (невырожденным) газом, то каждый электрон обладал бы энергией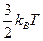 
, а энергия электронного газа, заключенного в одном моле металла, была бы равна 
; его теплоемкость - 
. Таким образом общая теплоемкость металла в области больших температур должна быть равна, согласно (2.26), 
.
В действительности металлы и диэлектрики в области высоких температур, в которой выполняется закон Дюлонга и Пти, установленный еще в 1819 г., обладают теплоемкостью ~ 
. Получается так, что электронный газ практически не вносит заметного вклада в общую теплоемкость. Этот результат совершенно непонятный с классической точки зрения нашел свое объяснение в квантовой теории.
Действительно, обратившись к функции плотности состояний 
, можно качественно объяснить теплоемкость электронного газа (рис.).
Когда мы нагреваем образец от абсолютного нуля, не каждый электрон в нем приобретает энергию ~ 
, как следовало бы из классической теории газов. Испытывают тепловое возбуждение и приобретают энергию ~ лишь электроны, находящиеся в состояниях с энергией в интервале вблизи уровня Ферми.
Если 
- полное число электронов, то тепловое возбуждение при повышении температуры от 0 до 
может испытать только часть электронов порядка отношения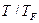 
, потому что приблизительно такая их доля 
обладает энергиями в энергетическом интервале в верхней части энергетического распределения.
Каждый из 
электронов обладает избыточной тепловой энергией порядка , а полная энергия 
теплового возбуждения электронов составляет величину порядка
.
Электронную теплоемкость получим, взяв производную по температуре от полной энергии теплового возбуждения
. (2.27)
Таким образом электронная теплоемкость ~ ; при комнатной температуре много меньше значения 
, которое дает классическая теория, примерно в 100 раз.
Получим более точное выражение для электронной теплоемкости, справедливое для области низких температур, удовлетворяющее условию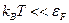 
. Полное изменение энергии системы электронов (рис.) представим в виде двух частей:
. (2.28)
Здесь 
- функция Ферми-Дирака, - число состояний на единичный энергетический интервал. Число частиц 
умножим на 
, в результате получим:
. (2.29)
Теперь продифференцируем (2.28) и (2.29) по :
, (2.30)
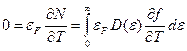. (2.31)
Вычтем (2.31) из (2.30); тогда для электронной теплоемкости получим:
. (2.32)
При низких температурах (
, для которых и ведется рассмотрение, производная 
велика только при энергиях близких к , и поэтому вместо функции можно взять ее значение при 
и вынести ее из под знака интеграла; в результате получим:
. (2.33)
В приближении первого порядка по температуре в выражении для функции распределения Ферми - Дирака химический потенциал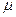 
можно заменить постоянной величиной 
. Тогда
,
вводя обозначение 
можно переписать (2.33)
. (2.34)
Так как 
в подинтегральном выражении пренебрежимо мало, то можно нижний предел в интеграле заменить на - 
. Получающийся определенный интеграл – табличный:
(2.35)
Теперь для получим:
. (2.36)
Для свободного электронного газа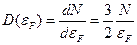 
, отсюда для получим:
. (2.37)
Этот результат находится в согласии с качественным результатом (2.27). Таким образом, сравнивая и 
, получим
, (2.38)
где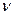 
- число молей. Так электронный газ в металлах является вырожденным, термическому возбуждению даже в области высоких температур подвергается лишь незначительная доля свободных электронов (~ 1%); остальные электроны энергию не поглощают. Иначе обстоит дело в области низких температур, близких к абсолютному нулю. В этой области теплоемкость решетки с понижением температуры падает ~ 
и вблизи абсолютного нуля может оказаться столь малой, что основное значение может приобрести , которая с понижением температуры падает значительно медленнее ( ~ ). На рис. приведена температурная зависимость теплоемкости сплава (20%V+80% Сr).