Проектирование гибких фундаментов
При расчете жестких фундаментов была принята линейная зависимость распределений напряжений под подошвой фундамента. При расчете фундаментов конечной жесткости (гибких фундаментов- балок и плит) условная линейная эпюра распределения напряжений под подошвой гибкого фундамента не приемлема.
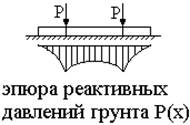В этом случае необходимо учитывать M и Q, возникающие в самой конструкции фундамента, вследствие действия неравномерных контактных реактивных напряжений по подошве фундамента. Не учет возникающих усилий может привести к неправильному выбору сечения фундамента или % его армирования.
Поэтому необходимо решать задачу совместной работы фундаментной конструкции и сжимаемого основания.
Какие же фундаменты считать гибкими?
Гибкие фундаменты - это те, деформации изгиба которых того же порядка, что и осадки этого же фундамента
∆ S(см) ≈ f(см); ∆ S – осадка фундамента (деформация основания)
f – деформация изгиба фундамента
Таким образом, при расчете гибких фундаментов необходимо одновременно учитывать и деформации фундамента и его осадки.
Конструкция грунт
При расчете ленточных фундаментов, загруженных неравномерно сосредоточенными силами - необходимо учитывать изгиб в продольном направлении.
Вследствие изгиба фундамента конечной жесткости давление на грунт увеличивается в местах передачи фундаменту сосредоточенных сил и уменьшается в промежутках между этими силами.
Единого метода расчета гибких фундаментов нет, а существует несколько способов.
|
h > 
- абсолютно жесткие фундаменты
h <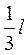 
- гибкие фундаменты
|
|
Метод прямолинейной эпюры
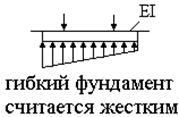
Области применения:
1 - для предварительных расчетов;
2 - когда не требуется большой точности расчетов;
3 - при слабых сильно сжимаемых грунтах;
Пример:
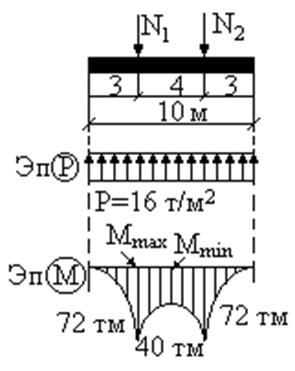
N1 =N2=80 т
b=1м
Определение ординаты эпюры
Контактного напряжения
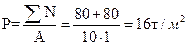
2. 
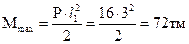
3. 
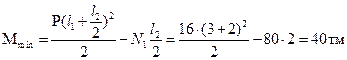
4. Определяем высоту балки
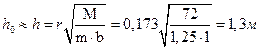где
r - коэффициент, зависящий от от % армирования;
m - коэффициент условий работы.
2. Теория местных упругих деформаций.
(Гипотеза Фусса-Винклера) 1868г.
Основная предпосылка этой теории – прямая
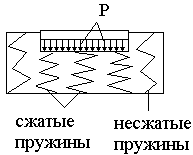пропорциональность между давлением и местной осадкой.
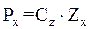; где Px – давление на подошве фундамента
Сz – коэффициент упругости основания
(коэффициент постели)
Zx – упругая осадка грунта в месте приложения
нагрузки
Эта модель хорошо отражает работу конструкции, если основание представлено жидкостью. Поэтому чаще всего этот метод при строительстве на слабых грунтах или в случае малой мощности слоя сжимаемого грунта.
В последнее время было предложено несколько методов, усовершенствующих эту модель: Дутов, Крылов, Кузнецов, Пастернак. Однако модели соответствующие гипотезе Фусса-Винклера не в состоянии учитывать разновидность оснований (изменение Ео по глубине и в плане сооружения).
В действительности эти результаты непосредственных наблюдений показали, что оседает не только нагруженная поверхность, но и соседние участки грунта.
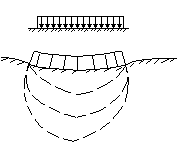Грунт деформируется в соответствии с упругим полупространством. Поэтому была выдвинута другая теория.
|
|
3. Теория общих упругих деформаций.
(Гипотеза упругого полупространства)
В основу этой теории положено предположение, что грунт является однородным и изотропным.
Это дало возможность применить к описанию напряженно деформируемого состояния аппарат теории упругости.
Рассмотрим осадку штампа:
 |
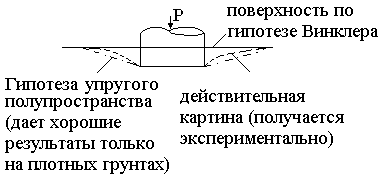Поэтому единого критерия расчета не существует. В каждом конкретном случае необходимо индивидуально подходить к поставленной задачи, оценивая жесткость конструкции и деформируемость основания. И только после этого следует выбирать руководствующую теорию для расчета.
Задачи, рассматриваемые на основании расчета теории балок