| Δt, часов | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | 700-800 | 800-900 |
| Σr(Δt) | |||||||||
| r(t) | |||||||||
| P(t) | 0,987 | 0,971 | 0,942 | 0,894 | 0,869 | 0,812 | 0,767 | 0,726 | 0,657 |
| Q(t) | 0,013 | 0,029 | 0,058 | 0,106 | 0,131 | 0,188 | 0,233 | 0,274 | 0,343 |
| a(Δt)∙10-4 | 1,224 | 1,632 | 2,857 | 4,897 | 2,449 | 5,714 | 4,449 | 4,081 | 6,938 |
| λ(Δt)∙10-4 | 1,232 | 1,667 | 2,983 | 5,333 | 2,778 | 6,796 | 5,685 | 5,464 | 10,029 |
| ω(Δt) | 11,016 | 14,688 | 25,713 | 44,073 | 22,041 | 51,426 | 40,041 | 36,729 | 62,442 |
ВЕРОЯТНОСТНАЯ ОЦЕНКА ПОКАЗАТЕЛЕЙ НАДЁЖНОСТИ
Рассчитать численные значения статистических характеристик для нормального закона распределения случайных величин (время работы до отказа). Построить гистограмму распределения времени работы до отказа объекта, полигон фактической и расчётной вероятностей отказа, а также графики изменения интегральной функции вероятности отказа и безотказной работы.
Проверить выдвинутую гипотезу с помощью критерия Пирсона.
Решение.
Время работы объекта до отказа l, мес., представлено в табл.2.1.
Таблица 2.1
| 135,3 | 114,7 | 23,5 | 76,7 | 49,3 | 157,1 | 95,3 | 86,1 | 139,1 | 146,3 |
| 48,2 | 92,3 | 104,1 | 112,3 | 28,6 | 88,1 | 79,5 | 102,7 | 119,4 | 51,5 |
| 115,4 | 50,1 | 64,3 | 18,2 | 99,7 | 64,5 | 126,5 | 86,3 | 88,2 | 39,4 |
| 95,6 | 62,7 | 90,1 | 76,3 | 137,8 | 106,8 | 59,8 | 83,5 | 69,3 | 108,2 |
1. Случайные величины располагаем в порядке возрастания.
lmin = 18.2; 23.5; 28.6; 39.4; 48.2; 49.3; 50.1; 51.5; 59.8; 62.7; 64.3; 64.5; 69.3; 76.3; 76.7; 83.5; 86.1; 86.3; 88.1; 88.2; 90.1; 92.3; 95.6; 99.7; 102.7; 104.1; 106.8; 108.2; 112.3; 114.7; 115.4; 119.4; 135.3; 137.8; 139.1; 146.3; lmax = 157.1 месяцев.
2. Определяем размах случайной величины R, мес.:
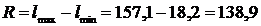(2.1)
3. Определяем количество интервалов, на которое следует разбить статистических ряд случайных величин.
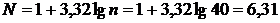(2.2)
где n – число значений в статистической совокупности случайных величин согласно заданию.
Округляем полученное значение до целого в большую сторону, т.е.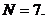 
4. Находим ширину интервала А, мес.:
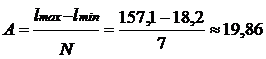. (2.3)
Принимает ширину интервала А равной 20 месяцев, поэтому статистический ряд разбиваем на 7 равных по величине интервалов. Для удобства последующих построений и расчётов длину интервала А следует принимать кратной пяти, т.е. 5, 10, 15 месяцев и т.д.
Результаты заносим в табл.2.2 (2 столбец). В 3 столбец заносим середины интервалов lсерi, мес.
5. Производим группировку, т.е. определяем число случайных величин в первом, втором и последующих интервалах. Количество случайных величин, попавших в определенный интервал называется частотой mi. Полученные результаты также заносим в табл.2.2 (4 столбец). С учётом имеющихся данных, строим гистограмму распределения времени работы объекта до отказа (рис.2.1, а).
Таблица 2.2
Сводная таблица статистической оценки времени работы
Объекта до отказа
| Номер интер-вала Ni | Интер-вал ∆ l, мес. | Сере-дина интер-вала lсерi, мес. | Час-тота, mi, шт. | Часто-сть, ωi → рi | Дифферен-циальная функция распреде-ления f(li) | Вероят-ность Рi* | Оценка накопленных вероятностей | |
| отказа Fi | безотказ-ности Ri | |||||||
| 1. | 0-20 | 0,025 | 0,0044 | 0,079 | 0,079 | 0,921 | ||
| 2. | 20-40 | 0,075 | 0,0061 | 0,109 | 0,188 | 0,812 | ||
| 3. | 40-60 | 0,125 | 0,0076 | 0,137 | 0,325 | 0,675 | ||
| 4. | 60-80 | 0,175 | 0,0085 | 0,152 | 0,477 | 0,523 | ||
| 5. | 80-100 | 0,25 | 0,0088 | 0,158 | 0,635 | 0,365 | ||
| 6. | 100-120 | 0,2 | 0,0081 | 0,146 | 0,781 | 0,219 | ||
| 7. | 120-140 | 0,1 | 0,0068 | 0,122 | 0,903 | 0,097 | ||
| 8. | 140-160 | 0,5 | 0,0053 | 0,095 | 0,998 | 0,002 | ||
| Всего | - | - | 0,0556 | 0,998 | - | - |
6. Определяем частость ωi. Частость является эмпирической величиной и служит для оценки вероятности. Как было отмечено ранее, при увеличении числа наблюдений частость приближается к вероятности: ωi → рi.
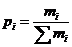, (2.4)
;
;
;
;
;
;
;
;
.
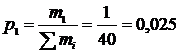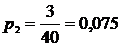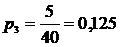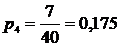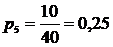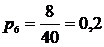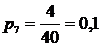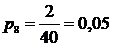Полученные при группировке времени работы объекта до отказа сводим в табл.2.2 (столбец 5).
7. Определяем среднее значение времени работы до отказа объекта М, мес., т.е.
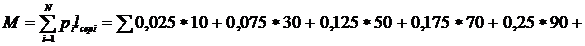
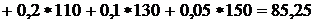. (2.5)
8. Определяем среднеквадратическое отклонение σ, мес.:
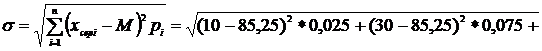(2.6)
.
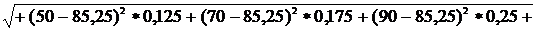
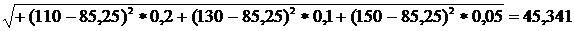9. Определяем коэффициент вариации υ:
.
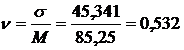Находим значения дифференциальной функции распределения. С учётом того, что значение коэффициента вариации υ <0,4, для заданной статистической совокупности предпочтителен нормальный закон распределения, т.е.
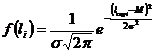, (2.7)
; 
; 
; 
; 
; 
; 
; 
;
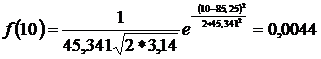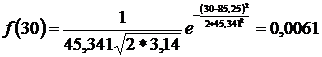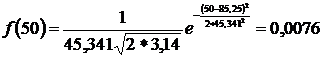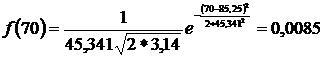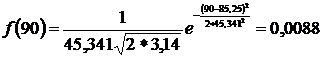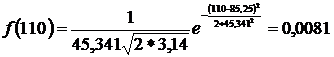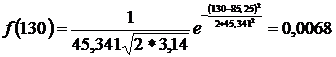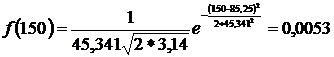Для упрощения расчётов можно принять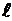 
= 2,718.
Найденные значения заносим в 6 столбец табл.2.2.
10. Определяем вероятность отказа Рi*, т.е. отношение числа случаев, благоприятствующих возникновению событий, к общему числу случаев:
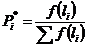, (2.8)
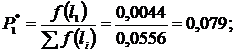
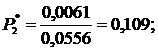
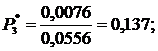
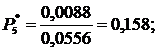
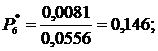
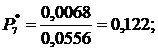
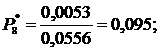
Найденные значения заносим в 7 столбец табл.2.2.
11. Определяем вероятность отказов Fi, которая может быть получена суммированием интервальных вероятностей за наработку li:
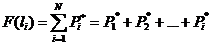, (2.9)
;
;
;
;
;
;
;
.
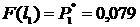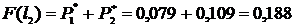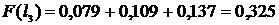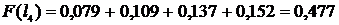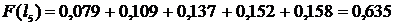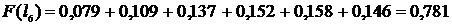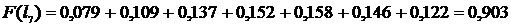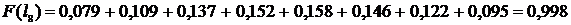
Полученные значения заносим в 8 столбец табл.2.2.
12. Определяем вероятность безотказности работы Ri:
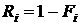, (2.10)
;
;
;
;
;
;
;
;
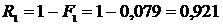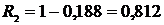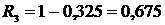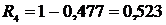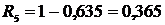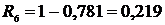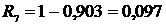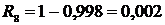Полученные значения заносим в 9 столбец табл.2.2.
По данным табл.3.2 строим графики: 
; 
; 
; 
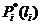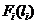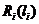(рис.3.2 б, в). Для удобства данные графики располагаем непосредственно под гистограммой распределения времени работы объекта до отказа.
 |
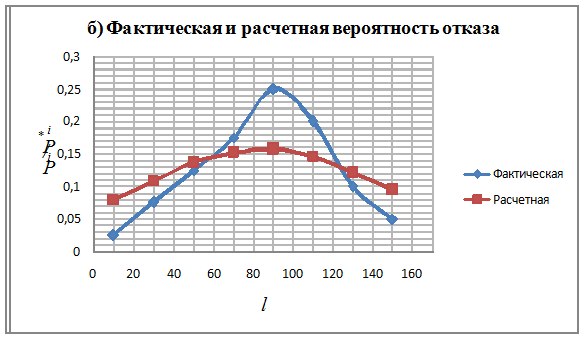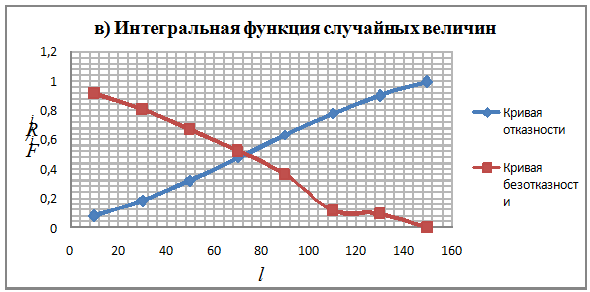
Рис.2.1. Графическое изображение времени работы до отказа объекта,
как случайной величины