Типовой расчет 1
Найдите максимальное и минимальное назначение для задачи с матрицей
| N | 2N | |||
| N | N |
Решение
Найдем максимальное назначение
Шаг 1:
Преобразуем матрицу, заменив каждый элемент матрицы разностью максимального элемента этой строки и самого элемента.
| Max=7 | |||||
| Max=8 | |||||
| Max=9 | |||||
| N | 2N -2 | 2N -9 | 2N -8 | Max=2N | |
| N -8 | N -7 | N -9 | Max=N |
Шаг 2.
Требуется получить нули в каждой строке и в каждом столбце. В первом, и третьем столбцах нулей нет, вычтем из элементов этих столбцов минимальный элемент соответствующего столбца.
| N-1 | 2N -2 | 2N -11 | 2N -8 | |
| N -9 | N -9 | N -9 |
Шаг 3.
Получили матрицу, в которой в каждой строки и каждом столбце есть ноль. Нашей целью является отметить по одной ячейке в каждой строке и каждом столбце так, чтобы они были нулевые. Отметим соответствующие ячейки желтым цветом.
| N-1 | 2N -2 | 2N -11 | 2N -8 | |
| N -9 | N -9 | N -9 |
Получили матрицу с пятью нулями, по одному в каждой строке и столбце, следовательно, можно провести назначения (распределение работ и т.д.) по матрице:
И стоимость (рациональность, время работ и т.д.) такого назначения составит: 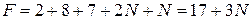
Найдем минимальное назначение
| N | 2N | |||
| N | N |
Шаг 1:
Преобразуем матрицу, заменив каждый элемент матрицы разностью самого элемента и минимального элемента строки.
| N-2 | 2N-2 | |||
| N-7 | N-7 |
Шаг 2.
Требуется получить нули в каждой строке и в каждом столбце. В четвертом, и пятом столбцах нулей нет, вычтем из элементов этих столбцов минимальный элемент соответствующего столбца.
| N-2 | 2N-4 | |||
| N-7 | N-10 |
Шаг 3.
Получили матрицу, в которой в каждой строки и каждом столбце есть ноль. Нашей целью является отметить по одной ячейке в каждой строке и каждом столбце так, чтобы они были нулевые. Отметим соответствующие ячейки желтым цветом.
| N-2 | 2N-4 | |||
| N-7 | N-10 |
Не удалось отметить 0 в четвертой строке.
Проводим модификацию матрицы. Вычеркиваем строки и столбцы с возможно большим количеством нулевых элементов: строки 5,3 столбец 2,
Получаем сокращенную матрицу (элементы не выделены).
| N-2 | 2N-4 | |||
| N-7 | N-10 |
Минимальный элемент сокращенной матрицы (1) вычитаем из всех ее элементов:
| N-3 | 2N-5 | ||||
| N-7 | N-10 |
Затем складываем минимальный элемент с элементами, расположенными на пересечениях вычеркнутых строк и столбцов:
| N-3 | 2N-4 | |||
| N-6 | N-10 |
Получили матрицу, в которой в каждой строки и каждом столбце есть ноль. Нашей целью является отметить по одной ячейке в каждой строке и каждом столбце так, чтобы они были нулевые. Отметим соответствующие ячейки желтым цветом.
| N-3 | 2N-4 | ||||
| N-6 | N-10 | ||||
Получили матрицу с пятью нулями, по одному в каждой строке и столбце, следовательно, можно провести назначения (распределение работ и т.д.) по матрице:
И стоимость (рациональность, время работ и т.д.) такого назначения составит: 
Типовой расчет 2. Решите задачу коммивояжера жадным алгоритмом и алгоритмом удвоения ребер минимального остова для матрицы расстояний между всеми парами из пяти вершин.
| N | ||||
| N |
Решение
Самый очевидный алгоритм решения задачи коммивояжера — жадный: из текущего города иди в ближайший из тех, куда ещё не ходил. Если выполняется неравенство треугольника, нетрудно доказать, что этот алгоритм ошибается не более, чем в два раза. Трудоемкость этого алгоритма O (V 2).
Запускаем жадный алгоритм из вершины 1, кратчайшее расстояние до вершины 3, равное 1. Из вершины 3 кратчайшее расстояние до вершины 2(за исключением уже посещенной вершины 1) равное 3. Из вершины 2 кратчайшее расстояние(до оставшихся вершин 4 и 5) расстояние до вершины 4, равное 6, от вершины 4 до вершины 5 расстояние равно N. Расстояние от вершины 5 до вершины 1 равно 7. Длина полученного цикла 1,3,2,4,5,1 равна 1+3+6+N+7=N+17.
Построим дерево-остов минимального веса с помощью алгоритма Прима.
Алгоритм Прима обладает тем свойством, что ребра в множестве А всегда образуют единое дерево. Дерево начинается с произвольной корневой вершины г и растет до тех пор, пока не охватит все вершины в V. На каждом шаге к дереву А добавляется легкое ребро, соединяющее дерево и отдельную вершину из оставшейся части графа. Данное правило добавляет только безопасные для А ребра; следовательно, по завершении алгоритма ребра в А образуют минимальное остовное дерево. Данная стратегия является жадной, поскольку на каждом шаге к дереву добавляется ребро, которое вносит минимально возможный вклад в общий вес.
Начнем с вершины с номером 1, добавим ребро {1,3}, которое имеет минимальный вес среди ребер, инцидентных вершине 1равный 1, затем ребро {3,2} веса 3, {2,4} веса 6, {4,5} веса N получим минимальное дерево-остов Т.Построим мультиграф, путем удвоения ребер в дереве Т.

Рис.1
Длина полученного цикла равна 1+3+6+N+N+6+3+1=2N+20.
Типовой расчет 3,4. Задан следующий орграф.
Дуга (s,v1) c весом 8, дуга(s,v2) c весом 9, дуга (v1, v2) c весом N, дуга (v1,t) c весом 4, дуга (v2,t) c весом 1, дуга (s,t) c весом 20. Найдите максимальный поток и минимальный разрез в сети, считая вес дуги ее пропускной способностью. Найдите минимальный путь из вершины s в вершину t.
Решение.
Нарисуем граф.

Рис.1.
Простой, связный орграф G будем называть транспортной сетью (или просто сетью), если выполняются следующие условия: - существует вершина s (источник), в которую не входит ни одна дуга, - существует вершина t (сток), из которой не выходит ни одна дуга, - каждой дуге eij приписано целое число сij≥0, называемое пропускной способностью дуги. Потоком в сети называют функцию, сопоставляющую каждой дуге целое неотрицательное число fij≥0(значение потока через дугу) так, чтобы
1) fij≤ сij, т.е. не превышало пропускной способности дуги
2) Для каждой промежуточной вершины (любой вершины, кроме s и t) выполнялось условие: сумма значений потоков по входящим в вершину дугам была равна сумме значений потоков по исходящим из неё дугам.
3) Для вершины s сумма исходящих потоков равна сумме потоков, входящих в вершину t.
Величиной потока, обозначают Val f, называют сумму значений потока на всех дугах, выходящих из источника s, равную сумме значений потока на всех дугах, входящих в сток t. Поток называется максимальным, если его величина наибольшая из возможных. Дуга eij называется насыщенной, если fij= сij, т.е. значение потока через дугу равно пропускной способности дуги.
Теорема Форда – Фолкерсона. Величина максимального потока в сети из вершины s в вершину t равна величине минимального сечения между этими вершинами.
Алгоритм Форда – Фолкерсона:
1. Зададим произвольный начальный поток, можно нулевой.
2. Вершину s пометим двойной пометкой: (0;∞). Первая пометка означает вершину, из которой получена пометка. Вторая нужна для подсчёта возможного увеличения потока. Дальнейшее помечивание по существу означает поиск пути из s в t.
3. Если в графе существует непомеченная вершина j, смежная с какой – то помеченной вершиной i, то в зависимости от того, как ориентирована связывающая их дуга, проводим прямую пометку (если дуга ведёт от i к j, и не насыщенная fij< сij) или обратную (если дуга ведёт от j к i, и cji>0). Прямая пометка: (+i, ∆j=cij-fij) Обратная пометка: (-i, ∆j=cij+fij)
4. Если на шаге 3 не удалось пометить вершины, выход из алгоритма, максимальный поток найден.
5. Если j=t, переход к 6, иначе переход к 3.
6. Этот шаг соответствует построенному пути из s в t, на котором возможно увеличение потока на величину ∆=min∆j, где ∆j – вторые метки всех вершин этого пути, кроме s. Начинаем с t и движемся по пометкам назад к источнику. На прямых дугах (1-я метка со знаком +) увеличиваем значение потока на ∆. На обратных дугах уменьшаем значение потока на ∆; если в этом случае fji - ∆.
Для нашего случая
Val f= 4+1+20=25.
1). Путь из s в t по которому поток может быть увеличен, состоит из прямых дуг, соединяющих вершины: s=1→3→t=4. Пометки указанных вершин: s=(0;∞)→(+1;∆ v1=8-4=4)→ (+1;∆v2 =9-1=8)→ t. Получили граф

Рис.2.
Путь из s в t (рис.2), на котором возможно увеличение потока построить не удалось. До стока t не дошли. Вершина t не может быть помечена, все входящие в нее дуги насыщены, поэтому поток не может быть увеличен.
Значит поток f (рис.2) максимален. Найдём минимальное сечение. Помеченные вершины: Мs={1,2,3}. Непомеченные вершины: Мt={4}. Прямые насыщенные дуги, идущие из Мs в Мt: e34, e14, e24, образуют минимальное сечение: e34· e14· e24. Величина этого сечения равна 4+1+20=25 и совпадает с величиной максимального потока f.