Пусть  — произвольное натуральное число. Будем называть его модулем.
— произвольное натуральное число. Будем называть его модулем.
Определение: Целые числа a и b сравнимы по модулю m, если их разность a - b делятся на m.
Обозначение: a ≡ b (mod m).
Пример:
17 ≡ 5 (mod 17), 19 ≡ -1 (mod 10)
15 ≡ 0 (mod 5), 11≡ 1 (mod 5)
Замечание: Сравнение 17 ≡ 5 (mod 12) иллюстрирует хорошо знакомую ситуацию. По модулю 12 мы обычно называем время, говоря "сейчас 5 часов", вместо "сейчас 17 часов".
Теорема 1: Следующее утверждения для целых чисел a и b равносильны:
1) разность a - b делится на m.
2)  , где
, где  .
.
3) a и b имеют одинаковые остатки при делении на m.
Доказательство: 1)  2) Пусть a - b делятся на m. Тогда a - b=mt
2) Пусть a - b делятся на m. Тогда a - b=mt
или  .
.
2)  3) Пусть
3) Пусть  , и пусть b при делении на m имеет остаток r, т.е.
, и пусть b при делении на m имеет остаток r, т.е.  . Тогда
. Тогда  , где 0 ≤ r < m.
, где 0 ≤ r < m.
Следовательно r — остаток от деления a на m. Значит, a и b имеют равные остатки от деления на m.
3)  1) Пусть
1) Пусть 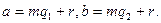 Тогда
Тогда  делится на m.
делится на m.
Доказанная теорема означает, что любое из трех равносильных утверждений можно принять за определение сравнения.
Перейдем к изучению свойств сравнений. Отношение сравнимости двух целых чисел является примером бинарного отношения на множестве Z. Во многом это отношение похоже на отношение равенства. Свойства 1°—4° иллюстрируют это сходство.
1°. Отношение сравнения является отношением эквивалентности:
- a ≡ a (mod m)
- a ≡ b (mod m)
 b ≡ a (mod m)
b ≡ a (mod m) - a ≡ b (mod m), b ≡ c (mod m)
 a ≡ c (mod m)
a ≡ c (mod m)
Доказательство:
1. Рефлексивно очевидна, т.к. a-a делиться на m.
2. Симметричность не менее ясна: если a-b делиться на m, то
b- a тоже делится на m.
3. Транзитивность следует из равенства  и свойств делимости.
и свойств делимости.
■
2°. Сравнения по одному и тому же модулю можно складывать, вычитать и умножать:
если a ≡ b (mod m), c ≡ d (mod m), то
a + c =b + d (mod m)
a - c =b – d (mod m)
a · c =b · d (mod m)
Доказательство: Пусть  ,
,  , где
, где 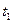 и
и  — целые.Тогда
— целые.Тогда

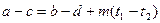

что по теореме 1 равносильно требуемым сравнениям.
■
Пример: 

3°. Обе части сравнения можно увеличить на одно и тоже число, домножать на одинаковый множитель или возвести в одинаковую степень:
если a ≡ b (mod m), то
a + k ≡ b + k (mod m), k 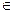 Z,
Z,
a · k ≡b · k (mod m), k 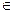 Z,
Z,
 (mod m), k
(mod m), k 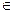 N.
N.
Доказательство: Требуемые утверждения легко получить, применяя свойство 2° к сравнениям a ≡ b (mod m) и
k ≡ k (mod m).
■
Пример: 9 ≡ 4 (mod 5 ). Для k = 2 получим верные сравнения:
11 ≡ 6 (mod 5 ), 18 ≡ 8 (mod 5 ), 81 ≡ 16 (mod 5 ).
4°. Члены сравнения можно переносить из одной части в другую с переменой знака:
a + b ≡ с (mod m)  a ≡ c-b (mod m)
a ≡ c-b (mod m)
Доказательство: Следует из свойства 3° при k = -b.
■
Следующие два свойства показывают отличие числовых сравнений от обычных равенств.
5°. В любой части сравнения можно добавить или отбросить слагаемое, кратное модулю:
a ≡ b (mod m)  a + m · k ≡ b (mod m)
a + m · k ≡ b (mod m)
Доказательство: По определению сравнимости:
m · k ≡ 0 (mod m). Складывая это сравнение с данным сравнением
a ≡ b (mod m) получим требуемое. Для доказательства обратного утверждения используем операцию вычитания.
■
Пример: Свойство 5° используют при подсчете дней недели:
3 ≡ b (mod 7)  24 ≡ b (mod 7).
24 ≡ b (mod 7).
Если 3 числа были вторник, то 24 числа тоже будет вторник.
6°. Обе части сравнения можно сократить на их общий множитель, если он взаимно прост с m:
если a · k ≡ b · k (mod m) и при этом НОД (k,m) = 1,
то a ≡ b (mod m).
Доказательство: Пусть a · k - b · k делится на m. По условию
k и m взаимно простые  a-b делиться на m
a-b делиться на m  a ≡ b (mod m).
a ≡ b (mod m).
■
Замечание: Условие взаимной простоты k и m очень важно. Вообще говоря, сокращение может привести к неверному результату. Например, 8 ≡ 6 (mod 2 ), но 4  3 (mod 2 ). Впрочем, иногда после сокращения на k результат может оказаться верным, хотя k и m не взаимно просты:
3 (mod 2 ). Впрочем, иногда после сокращения на k результат может оказаться верным, хотя k и m не взаимно просты:
Например, 85 ≡ 10 (mod 15 ).
После сокращения на 5 получим верное сравнение
17 ≡ 2 (mod 15 ).
Рассмотренные свойства сравнений обобщаются следующее теоремой.
Теорема 2: Пусть  — с целыми коэффициентами. Пусть x ≡ y (mod m).
— с целыми коэффициентами. Пусть x ≡ y (mod m).
Тогда p(x) ≡ p(y) (mod m).
Если, кроме того,  (mod m), i = 0,1,2…n, то
(mod m), i = 0,1,2…n, то
 (mod m).
(mod m).
Доказательство: Непосредственно следует из свойств2° и 3°.
Замечание 1: Аналогичная теорема верна и для многочленов от n переменных с целыми коэффициентами. Например,
если 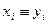 (mod m), i =1,2,3…n, то
(mod m), i =1,2,3…n, то
 (mod m).
(mod m).
Замечание 2: Встречающиеся в сравнении показатели степеней, нельзя заменять сравнимыми по модулю m. Иначе говоря, из того, что n ≡ k (mod m) не следует, что
 (mod m). Например, 3 ≡ 8 (mod 5 ), но
(mod m). Например, 3 ≡ 8 (mod 5 ), но 
 (mod 5 ), так как
(mod 5 ), так как 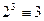 (mod 5 ), а
(mod 5 ), а  (mod 5 ).
(mod 5 ).
В свойствах 7° — 10° некоторые манипуляции проводят не только с обеими частями сравнения, но и с модулем m.
7°. Обе части сравнения и модуль можно домножить или сократить на их общий множитель:
a ≡ b (mod m)  a · k ≡ b · k (mod mk)
a · k ≡ b · k (mod mk)
Доказательство: Пусть a ≡ b (mod m). Тогда a = b + m∙t  a∙k = b∙k + m∙k∙t
a∙k = b∙k + m∙k∙t  a∙k ≡ b∙k (mod mk).
a∙k ≡ b∙k (mod mk).
Эти же рассуждения можно провести в обратном порядке.
■
8°. Если два числа сравнимы по модулю m, то они сравнимы по любому модулю d, делителю числа m:
 .
.
Доказательство: Если a-b делиться на m, а m делиться на d, то по транзитивности a-b делиться d  a ≡ b (mod d).
a ≡ b (mod d).
■
9°. Если два числа сравнимы по нескольким модулям, то они сравнимы по модулю, равному наименьшему общему кратному этих модулей:
 ,
,
где  .
.
Доказательство: Если 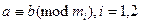 , то разность a-b делиться на
, то разность a-b делиться на  и на
и на  . Значит, (свойство 1 НОК) a-b делиться на
. Значит, (свойство 1 НОК) a-b делиться на  , т.е. a ≡ b (mod m). Такое же рассуждение сохраняет силу и для нескольких модулей.
, т.е. a ≡ b (mod m). Такое же рассуждение сохраняет силу и для нескольких модулей.
■
10°. Если a ≡ b (mod m), то множество общих делителей a и m совпадает с множеством общих делителей b и m. В частности НОД(a,m) = НОД(b,m).
Доказательство: Пусть a ≡ b (mod m). Тогда a – b = m∙t. Если d — общий делитель a и m, то  — общий делитель b и m. Обратное аналогично.
— общий делитель b и m. Обратное аналогично.
■