Теория сравнений дает в руки исследователя очень эффективный инструмент для решения теоретико − числовых задач. Проиллюстрируем его действенность несколькими элементарными примерами.
Пример 1: Найти остаток от деления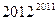 
на 7.
Решение: Имеем сравнение 2012 ≡ 612 ≡ -18 ≡ 3 (mod 7 ). Значит,
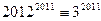(mod 7 )
Но 
, поэтому 
Ответ: остаток равен 3.
Пример 2: Доказать, что 
делится на 17 при всех 
.
Решение: Воспользуемся тем, что 25 
8 (mod 17 ). Имеем
Следовательно, данная сумма делится на 17.
Пример 3: Вывести признаки делимости на 9 и на 11.
Решение: Любое натурально число N можно записать в виде
Заметим, что 10 ≡ 1 (mod 9 ). Следовательно,
Число сравнимы по модулю 9, значит они имеют одинаковые остатки при делении на 9. В частности,
|| N делится на 9 
сумма цифр числа N делится на 9||
Аналогично, из сравнения 10 ≡ -1 (mod 11 ) следует, что
Отсюда следует, что
N делится на 11 Разность между суммой цифр числа N, стоящих на нечетных местах и суммой цифр, стоящих на четных местах, делится на 11.
Пример 4: Доказать, что уравнение 
не имеет решений в целых числах.
Решение: Любое решение x должно удовлетворять сравнению
При делении на 5 число x может иметь в остатке 0,1,2,3 и 4.
Но, так как
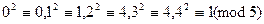
значит 
не может иметь остаток 3, т.е. сравнение не имеет решений.
Пример 5: Определить день недели по заданной дате.
Решение: Пусть N обозначает год, m — месяц, d — день
(1≤ m≤ 12), (1≤ d≤ 31) Первым месяцем года (m = 1 ) будем считать март, вторым (m = 2) — апрель и т.д. Тогда в високосные годы день 29 февраля добавляется в конце года, что удобно для расчета.
Обозначим ω — номер для недели (1≤ ω≤ 7), начиная отсчет с понедельника:
ω = 1 — Пн, ω = 2 — Вт, ω = 3 — Ср,…, ω=7 —Вс.
Пусть 
— номер того дня недели, который мы примем за точку отсчета. Напомним, что Россия перешла на григорианский календарь в феврале 1918 года, поэтому примем в качестве день недели 1 марта 1920 года. Таким образом, считаем
N ≥ 1920.
Пусть 
— номер дня 1 марта N -го года. Заметим, что
365 ≡ 1 (mod 7 ), поэтому каждый невисокосный год номер дня недели увеличивается на 1. Если же прошлый год был високосным, то к номеру дня недели добавим 2, т.к.
366 ≡ 2 (mod 7 ). Следовательно,
(mod 7 )
Упростив это выражение, получим
(mod 7 ),
(mod 7 ).
Вычислим . 1 марта 2012 года приходится на четверг, т.е. 
отсюда следует, что
(mod 7 ),
(mod 7 ).
Итак, 1 марта 1920 года был понедельник, следовательно,
(mod 7 ). (1)
Пусть теперь задано число d месяца m года N. Чтобы определить искомый день недели осталось вычислить количество дней, прошедших от 1 марта до заданной даты. Вычислим сначала номер дней недели для 1 числа каждого месяца.
В марте 31 день 
1 апреля имеет номер 
(mod 7 )
В апреле 30 дней 1 мая имеет номер 
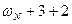(mod 7 )
и так далее, составим небольшую таблицу, в которой указано то слагаемое, которое нужно прибавит к .
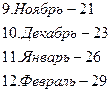
Номер возрастает примерно на 
в месяц. Поэтому нетрудно подобрать формулу
m = 1,2,3…,12
которая дает нужное добавочное слагаемое для любого месяца.
Итак, если ω — искомый день недели d числа m месяца N года, то к формуле (1) нужно прибавить и (d-1) — количество дней от 1 числа до нужной даты. В итоге получим
(mod 7 )
Определим, для примера день недели 22 июня 1941 года. Имеем N = 1941, m = 4, d = 22.
Итак, 22 июня 1941 года было воскресенье.