Шагающий аппарат содержит корпус, снабженный 2 ногами. В центре корпуса расположен гироскопический датчик, сообщающий системе управления информацию об ориентации корпуса по отношению к вектору силы тяжести; в передней части укреплен оптический дальномер, доставляющий информацию о поверхности, по которой перемещается шагающий робот. Внутри корпуса размещается микропроцессорная система управления и силовая часть.
Каждая конечность имеет три степени свободы, и приводится в действие с помощью двигателя с механизмом (передача, коробка передач, редуктор).

В нижней части конечности находятся три датчика усилия для измерения реакции силы ноги.
Основные характеристики шагающего аппарата:
· высота корпуса – 10 см; · длина стороны – 17 см;
· общая масса – 21 кг; · размер конечности – 45,6 см;
· масса конечности – 2.8 кг; · масса корпуса с микропроцессором – 3,8 кг;
· скорость – около 0,4 км/ч; · полезная нагрузка – 5 кг;
· длина бедра – 20,4 см; · длина голени – 25,2 см;
· поверхность касания конечности – 28,3 см2
Технические расчеты
Попытаемся произвести некоторые расчеты движения руки, ее координирования и различных сил действующих на нее.
Таким образом, вычисления во время рабочего режима при каждом периоде выборки включают в себя только вычисление сил и моментов, развиваемых приводами, но не включает преобразований из декартовой системы координат в пространство присоединенных переменных. Следовательно, возможно увеличение частоты выборки.
Пусть положение системы координат описывает однородная матрица Н(t), размерностью (4x4):
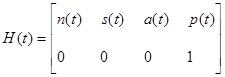
где p – вектор, описывающий положение манипулятора, n, s и a – вектора нормали, перемещения и подхода соответственно. Оценка сочленения, соответствующая матрице H(t), зависит от структуры робота. Один из примеров решения для манипулятора PUMA представлен ниже.
Пусть H(t)=H(t1). Схват должен пройти последовательность узловых точек в декартовом пространстве: H(t1), H(t2)…H(tn). Для построения траектории узловым точкам ставятся в соответствие векторы присоединенных координат [q11(t1), q12(t2), …,q1n(tn)],[ q21(t1), q22(t2), …,q2n(tn)],…[ q1n(t1), q2n(t2), …,qNn(tn)], где qji обозначает j-ю присоединенную переменную, соответствующую положению схвата в i-й узловой точке H(t). В данной процедуре построение траектории сочленения происходит для одного сочленения за один раз. Затем строится кубическая интерполяция траектории j-ой присоединенной переменной между точками qj1(t1), qj2(t2), …,qjn(tn). Индекс j в переменной qji не обязателен, поэтому qji ставим в соответствие qi.
Главная задача – построить траекторию j-ой присоединенной переменной во времени с использованием кубического полинома. Пусть t1<t2<…<tn-2<tn-1<tn – моменты прохождения узловых точек. В начальный момент t=t1 и конечный момент t=tn заданы соответственно начальные qj1, vj1, aj1 и конечные qjn, vjn, ajn (положение, скорость и ускорение). Кроме того, значения присоединенной переменной qjk в моменты времени tk заданы для k=3,4,…,n-2. Однако, значения q2 и qn-1 не фиксированы: как уже говорилось, это необходимо для обеспечения непрерывности кинематических характеристик вдоль всей траектории.
Пусть Qji(t) – кубический полином, описывающий поведение j-й присоединенной переменной между узловыми точками Hi и Hi+1 и определенный на интервале [t1, ti+1]. Задача состоит в “сшивке” между собой полиномов Qji(t) (i=1,2,…,n-1) так, чтобы они проходили через заданные узловые точки и обеспечивалась непрерывность положения, скорости и ускорения на всем интервале [t1, tn].
Поскольку Qji(t) – кубический полином, его вторая производная Q’’ji(t) должна быть линейной функцией времени t:
Q’’ji(t)=[(ti+1-t)/hi]*Q’’ji(ti) + [(t-ti)/hi]*Q’’ji(ti+1),
i=1,…,n-1, (1)
j=1,…,N,
где hi= ti+1-t – время, затрачиваемое на прохождение i-го участка. Дважды интегрируя Q’’ji(t) и учитывая граничные условия Qji(ti)=qji и Qji(ti+1)=qi,i+1, получаем интерполирующую функцию следующего вида:
Qji(t)= [(Q’’ji(ti)/6hi]*(ti+1-t)3 + (Q’’ji(ti+1)/6hi]*(t-ti)3 +
+ [qj,i+1/hi – hiQ’’ji(ti+1)/6](t-ti) + [qi,t/hi – hiQ’’ji(ti)/6](ti+1-t) i=1,2,…,n-1,
j=1,2,…,N. (2)
Таким образом, для i=1,2,…,n-1, Qji(t) определены, если известны Q’’ji(ti) и Q’’ji(ti+1). На основании этого можно записать систему n-2 линейных уравнений относительно неизвестных Q’’ji(ti), i=2,…, n-1,(описание системы в приложении А):
A=  , (3)
, (3)
A=  =
=
= 
Ленточная структура матрицы А позволяет легко определить неизвестную величину Q’’i(ti). В окончательном виде полиномы Qi’’(ti) выражаются временными интервалами hi и данными значениями присоединенных координат, скоростей и ускорений.
Доказательство единственного решения
Свойство 1: Задача интерполяции траектории имеет единственное решение, т.е. матрица А в уравнении (3) неособенная.
Доказательство: Известно, что hi – временные интервалы и должны быть положительны. Кроме того, в матрице А все строки, кроме 2 и n-3, удовлетворяют неравенству
 , для строки i. (4)
, для строки i. (4)
а) Если h2  h1 и hn-2
h1 и hn-2  hn-1, строки 2 и n-3 также будут удовлетворять неравенству (4). Поэтому, матрица А становится строго диагональной и неособенной.
hn-1, строки 2 и n-3 также будут удовлетворять неравенству (4). Поэтому, матрица А становится строго диагональной и неособенной.
б) Если h1 > h2, выполняем строковую операцию вычитания (строка 1)x(h2 – h21/h2)/(3h1+2h2+ h21/h2) из строки 2 для исключения а21.
Получаем:

и
 .
.
Из h1 >h2 следует, что  . Поэтому матрица А эквивалентна строго диагональной матрице. Следовательно, уравнение (3) имеет единственное решение.
. Поэтому матрица А эквивалентна строго диагональной матрице. Следовательно, уравнение (3) имеет единственное решение.
III.Описание траектории кубическими полиномами
В промышленности производительность зависит от скорости манипулирования робота. Для увеличения скорости работы манипулятора нужно минимизировать время движения вдоль заданной траектории. Задача оптимизации сводится к минимизации времени движения путем соответствующего выбора величин временных интервалов h1, h2,…, hn-1. с учётом ограничений присоединенных скоростей, ускорений, моментов и скоростей изменения ускорений. Для удобства примем:
VCj – ограничение по скорости для j-го сочленения,
wCj – ограничение по ускорению для j-го сочленения,
JCj – ограничение по скорости изменения ускорения для j-го сочленения.
Qji(t) – кубический полином, описывающий поведение j-й присоединенной переменной между узловыми точками i и i+1, т.е. между Hi и Hi+1.
wji – ускорение в Hi; оно соответствует Qji’’(ti) если Qji(t) проходит через Hi в момент времени ti.
X=(h1, h2,…, hn-1),- вектор временных интервалов.
Задачу можно сформулировать следующим образом: минимизировать целевую функцию Т

при следующих ограничениях:
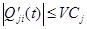 , j=1,2,…, N, i=1,2,…,n-1,
, j=1,2,…, N, i=1,2,…,n-1,
 , j=1,2,…, N, i=1,2,…,n-1,
, j=1,2,…, N, i=1,2,…,n-1,
 , j=1,2,…, N, i=1,2,…,n-1.
, j=1,2,…, N, i=1,2,…,n-1.
Строгое представление этих ограничений представлено ниже.
а) Ограничение по скорости.
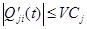 , j=1,2,…, N, i=1,2,…,n-1,
, j=1,2,…, N, i=1,2,…,n-1,
Дифференцируя равенство (2) и заменяя Qji’’(ti) и Qji’’(ti+1) соответственно на wji и wj,i+1, получаем:
Qji’(t)=wji/2hi*(ti+1-t)2 + wji+1/2hi*(t-ti)2 + [qj,i+1/hi – hiwj,i+1/6] – [qji/hi – hiwji/6],
Также Qji’’(t) можно представить как
Qji’’(t)= wj,i+1/hi*(t-ti) + wji/hi*(t-ti+1),
Скорость достигает своего максимального по абсолютной величине значения в одной из точек ti, ti+1 или  , где
, где  и Qji’’(
и Qji’’( )=0. Ограничение по скорости тогда принимает вид:
)=0. Ограничение по скорости тогда принимает вид:

для i=1,2,…,n-1j=1,2,…,N, (6)
где


И

б) Ограничения по ускорению:
 , j=1,2,…, N, i=1,2,…,n-1,
, j=1,2,…, N, i=1,2,…,n-1,
Между двумя узловыми точками ускорение линейно зависит от времени. Поэтому максимальная абсолютная величина ускорения достигается в точке ti или в точке ti+1 и равна максимальной из величин  .С учетом этого ограничение по ускорению принимает следующий вид:
.С учетом этого ограничение по ускорению принимает следующий вид:
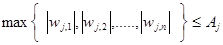 , j=1,2,…,N. (7)
, j=1,2,…,N. (7)
в) Ограничение по скорости изменения ускорения:
 , j=1,2,…, N, i=1,2,…,n-1.
, j=1,2,…, N, i=1,2,…,n-1.
Ограничение по скорости изменения ускорения можно представить в виде:
 j=1,2,…, N, i=1,2,…,n-1. (8)
j=1,2,…, N, i=1,2,…,n-1. (8)
Пример возможного решения
Свойство 2: Задача оптимизации при наличии ограничений (6) - (8) всегда имеет решение.
Если временные интервалы h1,…, hn-1 ….………., тогда, в соответствии со свойством 1 I-го раздела w2, w3,…, wn-1 определяются однозначно. Однако, ограничения по скорости, ускорению и скорости изменения ускорения могут не удовлетворять требованиям. В этом случае временные интервалы {h1,…, hn-1} могут быть увеличены для придания ограничениям значений, удовлетворяющих требованиям. Для этого представим Qi(t) исходным полиномом присоединенной переменной, определённым на временном интервале [ti, ti+1]=[ti, ti+hi]. Если все временные интервалы увеличить в соответствии с  так, что новые временные интервалы станут равными
так, что новые временные интервалы станут равными  , тогда, в соответствии с (5) новое ускорение wi* будет определено как wi*=wi/
, тогда, в соответствии с (5) новое ускорение wi* будет определено как wi*=wi/  . Таким образом, полином Qi(
. Таким образом, полином Qi(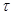 ), определенный на интервале [
), определенный на интервале [  ]=[
]=[  ], будет представлен новым полиномом Q*i(
], будет представлен новым полиномом Q*i( ). Первая, вторая и третья производные от Q*i(
). Первая, вторая и третья производные от Q*i( ) будут иметь вид (1/
) будут иметь вид (1/  )Qi’(
)Qi’( ), (1/
), (1/  )Qi’’(
)Qi’’( ) и (1/
) и (1/ 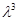 )Qi’’’(
)Qi’’’( ) соответственно. Предположим
) соответственно. Предположим
 , (9)
, (9)
 , (10)
, (10)
 , (11)
, (11)
и
 , (12)
, (12)
Если временной интервал hi заменен на  hi для i=1,2,…,n-1, тогда величины скорости, ускорения и скорости изменения ускорения будут уменьшены коэффициентами
hi для i=1,2,…,n-1, тогда величины скорости, ускорения и скорости изменения ускорения будут уменьшены коэффициентами  соответственно. Эти изменения обеспечат скорость, ускорение и скорость изменения ускорения значениями, отвечающими требованиям.
соответственно. Эти изменения обеспечат скорость, ускорение и скорость изменения ускорения значениями, отвечающими требованиям.  называется коэффициентом возможного регулирования. Процедура, выполняющая приведение некорректных величин к удовлетворяющему виду называется преобразователь возможного решения (ПВР). В итоге, процедура имеет вид:
называется коэффициентом возможного регулирования. Процедура, выполняющая приведение некорректных величин к удовлетворяющему виду называется преобразователь возможного решения (ПВР). В итоге, процедура имеет вид:
1) Вычисление  в уравнениях (9)-(12).
в уравнениях (9)-(12).
2) Замещение временных интервалов (h1, h2,…, hn-1) на ( ).
).
3) Замещение wj,2, wj,3,…, wj,n-1 на  соответственно. j=1,2,…, N.
соответственно. j=1,2,…, N.
Алгоритм оптимизации
Матрица А(Х) определена как вектор временных интервалов между выбранными узлами, т.е. [h1, h2,…, hn-1]. Основной задачей Х является представление Т(Х) и соответствует (h1+h2+…+hn-1). Сначала выбирается n – максимальное количество вершин Хi, (i=1,2,…, n), для формирования исходного многогранника. Пусть Xg и Xs имеют максимальное и минимальное значения функции. Предположим, что Хn+1 – центроид многогранника, не включая Хg. Вычисляется это так:

 . (13)
. (13)
Алгоритм пытается выбрать наилучшие значения (в соответствии с минимальным значением функции) вдоль прямой, соединяющей Xg и Xn+1, для замещения неудовлетвори-тельной величины Xg. Если это ему не удается, то многогранник уменьшается. Процедура поиска необходимых величин и уменьшения размера многогранника включает в себя отображение, растяжение, сжатие и уменьшение. Все они представлены ниже:
1)Отображение: Отображение Xg через центроид вычисляется следующим образом:
Xn+2=Xn+1+a(Xn+1-Xg), (14)
где а>0 – коэффициент отображения. Отметим, что все элементы Xn+2 являются временными интервалами. Для того, чтобы все интервалы были положительными, коэффициент а должен быть правильно определен. Сначала, примем его равным 1. Если какой-нибудь элемент Xn+2 будет отрицательным, то коэффициент следует уменьшить. Пусть Xp=[  ]. Для а=1 Xn+2 приобретает вид:
]. Для а=1 Xn+2 приобретает вид:
Xn+2=2Xn+1-Xg = [  ].
].
Все элементы должны быть положительными, т.е.  для всех i. Если
для всех i. Если  для какого-либо i, тогда уменьшаем коэффициент а.
для какого-либо i, тогда уменьшаем коэффициент а.
Из (14) получаем  . Если
. Если  , тогда
, тогда  . Следовательно, коэффициент а должен быть меньше, чем
. Следовательно, коэффициент а должен быть меньше, чем  , чтобы
, чтобы  был положительным. Учитывая все выше сказанное, коэффициент а может быть определен как:
был положительным. Учитывая все выше сказанное, коэффициент а может быть определен как:
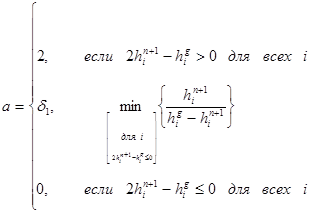 , (15)
, (15)
где 0<  <1 выбрана для того, чтобы убирать Xn+2 от границы, где хотя бы один элемент Xn+2 = 0.
<1 выбрана для того, чтобы убирать Xn+2 от границы, где хотя бы один элемент Xn+2 = 0.
2) Растяжение: Растянуть вектор (Xn+2-Xn+1) можно следующим образом:
Xn+3=Xn+1+  (Xn+2-Xn+1), (16)
(Xn+2-Xn+1), (16)
где  >1 – коэффициент растяжения. Для того, чтобы значения всех элементов Xn+3 были положительными, этот коэффициент должен быть определен следующим образом:
>1 – коэффициент растяжения. Для того, чтобы значения всех элементов Xn+3 были положительными, этот коэффициент должен быть определен следующим образом:
 , (17)
, (17)
где 0<  <1.
<1.
3) Сжатие: Сжать вектор (Xg-Xn+1) можно следующим образом:
Xn+4=Xn+1+  (Xg-Xn+1), (18)
(Xg-Xn+1), (18)
где 0<  <1 – коэффициент сжатия.
<1 – коэффициент сжатия.
4) Уменьшение: Уменьшить все вектора (Xi-Xs), i=1,2,…,n, деля их пополам начиная с Xs можно следующим образом:
 , i=1,2,…,n, (19)
, i=1,2,…,n, (19)
До начала поиска выберем n – максимальное количество вершин многогранника. Пусть qj,1, qj,3,…, qj,n-2, qj,n - присоединенные переменные, соответствующие положению схвата в j-й узловой точке. Из-за особенностей 2-ой и n-1 точек, qj,2 и qj,n-1 еще не определены. Временно они определены как qj,2=(qj,1+qj,3)/2 и qj,n-1=(qj,n-2+qj,n)/2. Таким образом, нижняя граница вектора временных интервалов оценивается как:
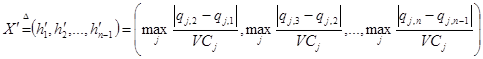 , (20)
, (20)
Первая вершина Х10 вычисляется как 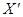 , если
, если  нам подходит, или обозначается как подходящая вершина, преобразованная процедурой (ПВР) из
нам подходит, или обозначается как подходящая вершина, преобразованная процедурой (ПВР) из  . Для вычисления остальных (n-1) вершин {
. Для вычисления остальных (n-1) вершин {  },
},  вычисляются как:
вычисляются как:
 , (21)
, (21)
где

D – выбранное расстояние. Поэтому,  вычисляется как
вычисляется как  , если
, если  нам подходит, или обозначается как подходящая вершина, преобразованная процедурой (ПВР) из
нам подходит, или обозначается как подходящая вершина, преобразованная процедурой (ПВР) из  . D влияет на размер многогранника.
. D влияет на размер многогранника.
Повторением операции мы уменьшаем размеры исходного многогранника и потом отслеживаем шаги поиска и приближения (к пределу). В процессе уменьшения многогранник иногда может принимать настолько малые размеры, что невозможно будет найти решение. Для возобновления процесса поиска мы будем использовать  , которая выбирает новый многогранник и новый процесс многократного уменьшения многогранника начинается заново. Размер многогранника определяется как
, которая выбирает новый многогранник и новый процесс многократного уменьшения многогранника начинается заново. Размер многогранника определяется как  . Если
. Если  будет меньше ранее определенного значения e1, то начнет выполняться новый цикл. Построение большего по размерам многогранника позволяет получить следующие преимущества:
будет меньше ранее определенного значения e1, то начнет выполняться новый цикл. Построение большего по размерам многогранника позволяет получить следующие преимущества:
1) Увеличение размера многогранника увеличивает шаг поиска на столько, чтобы он был способен достичь наилучшей вершины.
2) Форма многогранника изменяется в соответствии с направлением поиска.
Результаты двух следствий сравниваются. Цикл будет повторяться до тех пор, пока не возникнет каких-либо существенных различий между результатами, т.е. разность решений двух циклов будет меньше ранее определенного значения e2. Ниже представлен подробный алгоритм вычисления. LВ алгоритме, при достижении 14 шага, цикл завершается. На 13 шаге завершается стадия повторения этого цикла. Таким образом, kk – номер цикла, который начинается с 0, а k – номер стадии для каждого цикла, который тоже начинается с 0.
(Инициализация)
Шаг 1) Пусть kk=0 и k=0. Выбираем  и
и  в выражениях (15), (17) и (18). Также выбираем е1 и е2. Пусть OLDХs=[0,0,…,0].
в выражениях (15), (17) и (18). Также выбираем е1 и е2. Пусть OLDХs=[0,0,…,0].
(Вычисление первой вершины многогранника)
Шаг 2) Вычисляем  по (20). Если
по (20). Если  подходит, тогда
подходит, тогда  ; иначе, величине
; иначе, величине  присваивается подходящая вершина, преобразованная процедурой (ПВР) из
присваивается подходящая вершина, преобразованная процедурой (ПВР) из  .
.
(Вычисление остальных n-1 вершин многогранника)
Шаг 3) Для i=2,3,…,n вычисляем  по (21). Если
по (21). Если  подходит, тогда
подходит, тогда  ; иначе, величине
; иначе, величине  присваивается подходящая вершина, преобразованная процедурой (ПВР) из
присваивается подходящая вершина, преобразованная процедурой (ПВР) из  .
.
Шаг 4) Из n вершин  а) определяем
а) определяем  , которая принимает наименьшее значение функции и б)
, которая принимает наименьшее значение функции и б)  , которая принимает наибольшее значение функции. Из этого следует
, которая принимает наибольшее значение функции. Из этого следует  и
и  .
.
Шаг 5) Вычисляем центр многогранника  по (13).
по (13).
(Отображение)
Шаг 6) Проводим отображение для получения  с помощью (14) и (15). Полученную величину
с помощью (14) и (15). Полученную величину 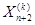 приводим к подходящему для нас виду процедурой (ПВР), если до этого она была не подходящей.
приводим к подходящему для нас виду процедурой (ПВР), если до этого она была не подходящей.
(Растяжение, при  )
)
Шаг 7) Если  , то выполняем а), б), и с) ………………………; иначе, переходим к шагу 8).
, то выполняем а), б), и с) ………………………; иначе, переходим к шагу 8).
а) Если  полагаем
полагаем  , потом увеличиваем k=k+1 и переходим на шаг 13),
, потом увеличиваем k=k+1 и переходим на шаг 13),
иначе продолжаем (Замечание:  показывает, что некоторые вершины многогранника в результате отображения имеют хоть и малые, но положительные значения. Растяжение нельзя проводить, т.к. они могут стать отрицательными, а это нарушает условие о положительных временных интервалов.
показывает, что некоторые вершины многогранника в результате отображения имеют хоть и малые, но положительные значения. Растяжение нельзя проводить, т.к. они могут стать отрицательными, а это нарушает условие о положительных временных интервалов.
б) Выполняем отображение для получения  по формулам (16) и (17). Приводим
по формулам (16) и (17). Приводим  к подходящему для нас виду процедурой (ПВР), если до этого она была не подходящей.
к подходящему для нас виду процедурой (ПВР), если до этого она была не подходящей.
с) Выбираем
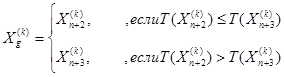
потом увеличиваем k=k+1 и переходим на шаг 13).
Шаг 8) Если  для некоторых
для некоторых  полагаем
полагаем  , потом увеличиваем k=k+1 и переходим на шаг 13).
, потом увеличиваем k=k+1 и переходим на шаг 13).
Шаг 9) Если  , тогда полагаем
, тогда полагаем  .
.
(Сжатие)
Шаг 10) Выполняем сжатие для получения величины 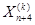 по формуле (18). Полученную величину
по формуле (18). Полученную величину  приводим к подходящему для нас виду процедурой (ПВР), если до этого она была не подходящей.
приводим к подходящему для нас виду процедурой (ПВР), если до этого она была не подходящей.
Шаг 11) Если 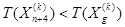 , тогда полагаем
, тогда полагаем  , потом увеличиваем k=k+1 и переходим на шаг 13), иначе продолжаем.
, потом увеличиваем k=k+1 и переходим на шаг 13), иначе продолжаем.
(Уменьшение)
Шаг 12) Уменьшаем многогранник следующим образом:
 , i=1,2,…,n.
, i=1,2,…,n.
(Проверка размера многогранника)
Шаг 13) Если  , тогда переходим на шаг 14), иначе переход на шаг 4).
, тогда переходим на шаг 14), иначе переход на шаг 4).
(Проверка на близость результатов решений двух циклов)
Шаг 14) Если  ,тогда
,тогда  выводим как результат и прекращаем поиск; иначе полагаем
выводим как результат и прекращаем поиск; иначе полагаем  ,
,  . Потом увеличиваем kk=kk+1, обнуляем k=0, и переходим на шаг 3).
. Потом увеличиваем kk=kk+1, обнуляем k=0, и переходим на шаг 3).
Алгоритм оптимизации всегда приводит не удовлетворяющую величину к подходя-щему для нас виду процедурой (ПВР), которая выполняет преобразование не удовлетворяющих величин умножением на величину  .Процедура преобразования занимает очень мало времени.
.Процедура преобразования занимает очень мало времени.
В начале каждого цикла n вершин первоначально определяются так, что любая из (n-1) вершин линейно независима. Новая вершина, которая замещает  , всегда представляет собой линейную комбинацию
, всегда представляет собой линейную комбинацию  и остальных n-1 вершин. Следовательно, любая из (n-1) вершин из нового выбора вершин n все еще линейно независима. Расположение исключает возможность того, что поиск попадет в подпространство.
и остальных n-1 вершин. Следовательно, любая из (n-1) вершин из нового выбора вершин n все еще линейно независима. Расположение исключает возможность того, что поиск попадет в подпространство.
Вычисление производной для 
Условие непрерывности по скорости дает нам  , i=1,2,…,n-1,что при использовании уравнений (1) и (2) приводит нас к уравнению вида:
, i=1,2,…,n-1,что при использовании уравнений (1) и (2) приводит нас к уравнению вида:
 , i=1,2,…,n-1. (22)
, i=1,2,…,n-1. (22)
Не оговоренные присоединенные переменные в двух особых точках могут быть выражены граничными величинами начальных и конечных узлов вместе с  и
и  . Следовательно,
. Следовательно,
 , (23)
, (23)
 (24)
(24)
Подставляя (23) и (24) в (22) получаем
 (25)
(25)
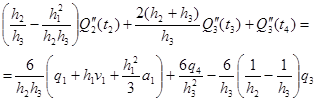 (26)
(26)
 (27)
(27)
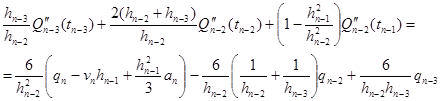 (28)
(28)
 (29)
(29)
Из-за условия непрерывности по ускорению в уравнениях (25) и (29)  примем равным
примем равным 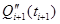 .Таким образом, (25) – (29) –система, состоящая из n-2 уравнений с n-2 неизвестными
.Таким образом, (25) – (29) –система, состоящая из n-2 уравнений с n-2 неизвестными  ,для i=2,3,…,n-1.
,для i=2,3,…,n-1.
ВЫВОДЫ
В представленной курсовой работе был разработан робот для разминирования различных объектов, рассчитаны его параметры и рабочие характеристики, которые были получены при моделировании в пакете прикладной программы Mathcad 2001.
В ходе данной разработке был проведен анализ задачи «Проектирование робота». Разработана структура функционирования и передвижения ноги робота.
В результате курсового проектирования была выполнена поставленная задача разработки исследуемого объекта.
ПЕРЕЧЕНЬ ССЫЛОК
1. Советов Б.Я., Яковлев С.А. “Робототехника”. - М.: Высш. шк., 2005.- 271 с.
2. Методические указания к курсовой работе по дисциплине "Робототехника и мехатроника" для студентов специальности ГКСР ". 1999.
3. Аш Ж., Андре П., Бофрон Ж. Датчики измерительных систем. В 2 т. Пер с фр. М.:Мир, 2002;
4. Бауман Э. Измерение сил электрическими методами: Пер. с нем. Мир, 1978. Энергоатомиздат, 2001;
5. Воротников С.А. Информационные устройства робототехнических систем. М.: Изд. МГТУ им. Н.Э.Баумана, 2005
6. Вульвет Дж. Датчики в цифровых системах: Пер. с англ. М.:Энергоиздат, 2003;
7. Гориневский Д.М. Формальский А.М., Шнейдер А.Ю. Управление манипуляционными системами на основе информации об усилиях. М.:Изд.фирма «Физико-математическая литература», 2001;
8. Погребной В.О., Рожанковский И.В., Юрченко Ю.П. Основы информационных процессов в роботизированном производстве;
9. Письменный Г.В., Солнцев В.И., Воротников С.А. Системы силомоментного очувствления роботов. М.: Машиностроение, 2000