Идея мемоизации очень проста — единожды вычисляя значение, мы заносим его в какую-то структуру данных. Перед каждым вычислением мы проверяем, есть ли вычисляемое значение в этой структуре, и если есть, используем его. В качестве структуры данных можно использовать массив, заполненный флаговыми значениями. Если значение элемента по индексу N равно значению флага, значит, мы его ещё не вычисляли.
Для уже написанной функции f(int) кэширование значений будет выглядеть следующим образом:
private static HashMap<Integer, Integer> cache = new HashMap<Integer, Integer>(); private static int fcashe(int n){ if(!cache.containsKey(n)){//Проверяем, находили ли мы данное значение cache.put(n, f(n)); //Если нет, то находим и записываем в таблицу } return cache.get(n);}
Мемоизация избавляет от огромного количества операций. Платите вы за это лишним расходом памяти.
Пример 2
На вершине лесенки, содержащей N ступенек, находится мячик, который начинает прыгать по ним вниз, к основанию. Мячик может прыгнуть на следующую ступеньку, на ступеньку через одну или через 2. (То есть, если мячик лежит на 8-ой ступеньке, то он может переместиться на 5-ую, 6-ую или 7-ую.) Определить число всевозможных «маршрутов» мячика с вершины на землю.
Идея решения
На первую ступеньку можно попасть только одним образом — сделав прыжок с длиной равной единице. На вторую ступеньку можно попасть сделав прыжок длиной 2, или с первой ступеньки — всего 2 варианта. На третью ступеньку можно попасть сделав прыжок длиной три, с первой или со втрой ступенек. Т.е. всего 4 варианта (0->3; 0->1->3; 0->2->3; 0->1->2->3). Теперь рассмотрим четвёртую ступеньку. На неё можно попасть с первой ступеньки — по одному маршруту на каждый маршрут до неё, со второй или с третьей — аналогично. Иными словами, количество путей до 4-й ступеньки есть сумма маршрутов до 1-й, 2-й и 3-й ступенек. Математически выражаясь, F(N) = F(N-1)+F(N-2)+F(N-3). Первые три ступеньки будем считать начальными состояниями.
Реализация через рекурсию
private static int f(int n){ if(n==1) return 1; if(n==2) return 2; if(n==3) return 4; return f(n-1)+f(n-2)+f(n-3);}Реализация через массив значений
Исходя из того, что, по большому счёту, простое решение на массиве из N элементов очевидно, продемонстрируем решение на массиве всего из трёх элементов.
int[] vars = new int[3];vars[0]=1;vars[1]=2;vars[2]=4; for(int i=3; i<N; i++){ vars[i%3] = vars[0]+vars[1]+vars[2]; }} System.out.println(vars[(N-1)%3]);Так как каждое следующее значение зависит только от трёх предыдущих, ни одно значение под индексом меньше i-3 нам бы не пригодилось. В приведённом выше коде мы записываем новое значение на место самого старого, не нужного больше. Цикличность остатка от деления на 3 помогает нам избежать большого количества условных операторов. Просто, компактно, элегантно.
Пример 3
В прямоугольной таблице NxM в начале игрок находится в левой верхней клетке. За один ход ему разрешается перемещаться в соседнюю клетку либо вправо, либо вниз (влево и вверх перемещаться запрещено). Посчитайте, сколько есть способов у игрока попасть в правую нижнюю клетку.
Идея решения
Логика решения полностью идентична таковой в задаче про мячик и лестницу — только теперь в клетку (x,y) можно попасть из клеток (x-1,y) или (x, y-1). Итого F(x,y) = F(x-1, y)+F(x,y-1). Дополнительно можно понять, что все клетки вида (1,y) и (x,1)имеют только один маршрут — по прямой вниз или по прямой вправо.
Реализация через рекурсию
«Двумерная динамику» через рекурсию как правило плохо представима или не имеет решения. Так как рекурсия менее выгодна, чем цикл по быстродействию, то двумерная рекурсия считается слишком медленно. Это только на таком простом примере она смотрится легко и безобидно.
private static int f(int i, int j) { if(i==1 || j==1) return 1; return f(i-1, j)+f(i, j-1);}Реализация через массив значений
int[][] dp = new int[Imax][Jmax]; for(int i=0; i<Imax; i++){ for(int j=0; j<Jmax; j++){ if(i==0 || j==0){ dp[i][j]=1; }else{ dp[i][j]=dp[i-1][j]+dp[i][j-1]; } }} System.out.println(dp[Imax-1][Jmax-1]);Классическое решение динамическим программированием, ничего необычного — проверяем, является ли клетка краем, и задаём её значение на основе соседних клеток.
Пример 4
Взрывоопасность
При переработке радиоактивных материалов образуются отходы двух видов — особо опасные (тип A) и неопасные (тип B). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A. Стопка считается безопасной, если она не является взрывоопасной. Для заданного количества контейнеров N определить количество возможных типов безопасных стопок.
Решение
Ответом является (N+1)-е число Фибоначчи. Догадаться можно было, просто вычислив 2-3 первых значения. Строго доказать можно было, построив дерево возможных построений.
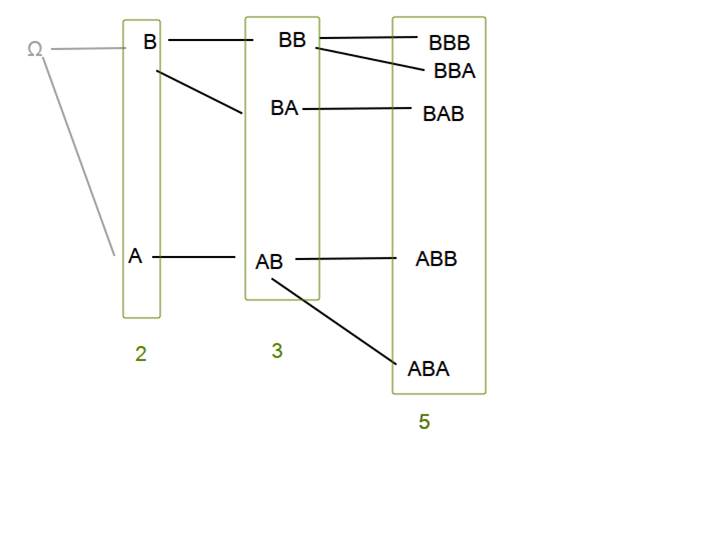
Каждый основной элемент делится на два — основной (заканчивается на B) и побочный (заканчивается на A). Побочные элементы превращаются в основные за одну итерацию (к последовательности, заканчивающейся на A, можно дописать только B). Это характерно для чисел Фибоначчи.
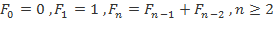
Программа
//Ввод числа N с клавиатуры N+=2; BigInteger[] fib = new BigInteger[2];fib[0]=fib[1]=BigInteger.ONE; for(int i=2; i<N; i++){ fib[i%2] = fib[0].add(fib[1]);} System.out.println(fib[(N-1)%2]);