Силы тяготения. Гравитационное поле

СИЛЫВ МЕХАНИКЕ

Основные формулы

• Закон всемирного тяготения

где F — сила взаимного притяжения двух материальных точек; m₁ и m₂ — их массы; r — расстояние между точками; G — гравита­ционная постоянная.

В написанной форме закон всемирного тяготения можно приме­нять и к взаимодействию шаров, масса которых распределена сфери­чески-симметрично. В этом случае r есть расстояние между центра­ми масс шаров.

• Напряженность гравитационного поля

где F — сила тяготения, действующая на материальную точку массы m, помещенную в некоторую точку поля.

• Напряженность гравитационного поля, создаваемого плане­той, массу М которой можно считать распределенной сферически-симметрично,

где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

• Ускорение свободного падения на высоте h над поверхно­стью Земли

где R — радиус Земли; g — ускорение свободного падения на по­верхности Земли. Если , то

• Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m₁ и m₂ (шаров с массой, распре­деленной сферически симметрично), находящихся на расстоянии r друг от друга,

(Потенциальная энергия бесконечно удаленных друг от друга ма­териальных точек принята равной нулю.)

• Потенциал гравитационного поля

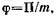
где П — потенциальная энергия материальной точки массой m, помещенной в данную точку поля.

• Потенциал гравитационного поля, создаваемого планетой, массу М которой можно считать распределенной сферически-сим­метрично,

где r — расстояние от центра планеты до интересующей нас точки поля, находящейся вне планеты.

• Законы Кеплера.

1. Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.

2. Радиус-вектор планеты в равные времена описывает одинако­вые площади.

3. Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит:

Законы Кеплера справедливы также для движения спутников вокруг планеты.

• Относительная деформация при продольном растяжении или сжатии тела

где ε — относительное удлинение (сжатие); x — абсолютное удли­нение (рис. 4.1); l — начальная длина тела.

Относительная деформация при сдвиге определяется из формулы

Рис. 4.1 Рис. 4.2

 

где — относительный сдвиг; Δs — абсолютный сдвиг параллель­ных слоев тела относительно друг друга (рис. 4.2); h — расстояние между- слоями; — угол сдвига. (Для малых углов )

• Напряжение нормальное

где Fynp — упругая сила, перпендикулярная поперечному сечению тела; S — площадь этого сечения.

Напряжение тангенциальное

где Fynp — упругая сила, действующая вдоль слоя тела; S — площадь этого слоя.

• Закон Гука для продольного растяжения или сжатия

или ,

где k — коэффициент упругости (в случае пружины — жесткость); Е — модуль Юнга.

Закон Гука для сдвига

, или ,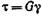

где G — модуль поперечной упругости (модуль сдвига).

• Момент, закручивающий на угол φ однородный круглый стер­жень,

,

где С — постоянная кручения.

• Работа, совершаемая при деформации тела,

• Потенциальная энергия растянутого или сжатого стержня

, или , или ,
где V — объем тела.

Примеры решения задач

Пример 1. Определить вторую космическую скорость υ₂ ракеты, запущенной с поверхности Земли.

Примечание. Второй космической (или параболической) скоростью υ2 называется минимальная скорость, которую нужно сообщить телу, чтобы оно удалилось с поверхности Земли в бесконечность (при этом сопротивление воздуха в расчет не принимается и предполагается, что на тело действует только поле тяготения Земли).

 

Решение. При удалении тела массой т в бесконечность его потенциальная энергия возрастает за счет убыли кинетической энер­гии и в бесконечности достигает максимального значения, равного нулю. Согласно определению второй космической скорости, кине­тическая энергия в бесконечности также равна нулю. Таким обра­зом, в бесконечности Т∞=0 и П∞ =0. В соответствии с законом сохранения энергии в механике

, или ,

где М — масса Земли. Отсюда находим Преобразуем эту формулу, умножив и разделив подкоренное выражение на R:

Так как (где g — ускорение свободного падения у
поверхности Земли), то

Подставив в эту формулу значения g и R и произведя вычисле­ния, получим

Пример 2. Ракета установлена на поверхности Земли для за­пуска в вертикальном направлении. При какой минимальной ско­рости υ₁, сообщенной ракете при запуске, она удалится от поверхности на расстояние, равное радиусу Земли ? Силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.

Решение. Чтобы определить минимальную скорость V₁ ра­кеты, надо найти ее минимальную кинетическую энергию T₁. Для этого воспользуемся законом сохранения механической энергии. Этот закон выполняется для замкнутой системы тел, в которой дей­ствуют только консервативные силы.

Систему ракета — Земля можно считать замкнутой. Единствен­ная сила, действующая на систему,— сила гравитационного взаи­модействия, являющаяся консервативной.

В качестве системы отсчета выберем инерциальную систему от­счета, так как только в такой системе справедливы законы динами­ки и, в частности, законы сохранения. Известно, что система отсчета, связанная с центром масс замкнутой системы тел, является инерциальной. В рассматриваемом случае центр масс системы ракета — Земля будет практически совпадать с центром Земли, так как масса М Земли много больше массы m ракеты. Следовательно, систему отсчета, связанную с центром Земли, можно считать практически инерциальной. Согласно закону сохранения механической энергии, запишем

(1)

где T₁ и П₁ — кинетическая и потенциальная энергия системы раке­та — Земля в начальном состоянии (на поверхности Земли); Т₁ и П₂ — те же величины в конечном состоянии (на расстоянии, равном радиусу Земли).

В выбранной системе отсчета кинетическая энергия Земли равна
нулю. Поэтому T₁ есть просто начальная кинетическая энергия
ракеты: 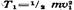. Потенциальная энергия системы в начальном
состоянии * .

По мере удаления ракеты от поверхно­сти Земли ее потенциальная энергия будет возрастать, а кинетиче­ская — убывать. В конечном состоянии кинетическая энергия Т₁ станет равной нулю, а потенциальная энергия П₂ достигнет макси­мального значения:

Подставив значения T₁, П₁, T₂ и П₂ в выражение (1), получим

откуда после сокращения на m найдем

Заметив, что (g — ускорение свободного падения у по­верхности Земли), перепишем эту формулу в виде

что совпадает с выражением для первой космической скорости (см. пример 1). Подставив числовые значения величин и произведя вычисления, получим

Пример 3. Найти выражение для потенциальной энергии П гра­витационного взаимодействия Земли и тела массой m, находящегося на расстоянии r от центра Земли за пределами ее поверхности. По­строить график П(r).

Решение. Потенциальная энергия в поле консервативных сил (гра-

витационные силы консервативны) связана с силой следую­щим соотношением:

* Потенциальная энергия гравитационного взаимодействия тел, беско­нечно удаленных друг от друга, принимается равной нулю

где i, j, k — единичные векторы осей координат (орты); —частные производные потенциальной энергии по соот­ветствующим координатам. В случае, когда поле сил обладает сфе­рической симметрией, это выражение упрощается. Если ось х совместить с радиусом-вектором r, направленным по радиусу сферы,

то и обращаются в нуль и тогда . Так как ве-­
кторы r и i совпадают (рис. 4.3) и П зави-­
сит только от r, то

(1)
Запишем в векторной форме закон все­ мирного тяготения:

 

 

Рис.4.3 (2)

где G — гравитационная постоянная; М — масса Земли.

Сравнивая выражения (1) и (2), найдем откуда

Взяв от этого равенства неопределенный интеграл, получим

где С — постоянная интегрирования.

Полученное выражение показывает, что потенциальная энергия может быть определена лишь с точностью до некоторой произволь­ной постоянной.

1. Если принять потенциальную энергию бесконечно удаленных друг от друга тел равной нулю, то постоянная С обращается в нуль. В этом случае запишем

 

Соответствующая зависимость П(r) изображается графиком, представленным на рис. 4.4.

2. Если же принять потенциальную энергию равной нулю на

поверхности Земли, то и тогда

Но так как r=R+h, где h — высота тела над поверхностью Земли, то

Если , то , или, так как ,

Пример 4. В гравитационном поле Земли тело массой m переме­щается из точки 1 в точку 2 (рис. 4.5). Определить скорость v₂ тела в точке 2, если в точке 1 его скорость

Ускорение свободного падения g считать известным.

Решение. Система те­ло — Земля является замкнутой, в которой действует

Рис. 4.5

 

Рис. 4.4

 

консервативная сила — сила гравитационного взаимодействия. Поэтому можно воспользоваться законом сохранения механической энергии (инерциальную систему отсчета свяжем с центром масс системы). Тогда можно записать

E₁=E₂, или T₁+П₁=Т₂+П₂,

где T₁, П₁ и Т₂, П₂ — соответственно кинетические и потенциальные
энергии в начальном 1 и конечном 2 состояниях. Заметим, что центр
масс системы тело — Земля практически совпадает с центром масс
Земли , и поэтому кинетическая энергия Земли в начальном
и конечном состояниях равна нулю. Тогда

Подставив эти выражения в (1), получим

Заменив и произведя сокращения, найдем
+ , откуда

Так как (по условию задачи), то

Произведя вычисления, получим

Пример 5. Вычислить работу А₁₂ сил гравитационного поля Земли при перемещении тела массой m= 10 кг из точки 1 в точку 2 (рис. 4.5). Радиус R земли и ускорение g свободного падения вблизи поверхности Земли считать известными.

Решение. Для решения задачи воспользуемся соотношением между работой А и изменением ΔП потенциальной энергии. Так как силы системы — гравитационные — относятся к силам консерва­тивным, то работа сил поля совершается за счет убыли потенциаль­ной энергии, т. е.

(1)

где П₁ и П₂ — потенциальные энергии системы тело — Земля соот­ветственно в начальном и конечном ее состояниях.

Условимся, что потенциальная энергия взаимодействия тела и Земли равна нулю, когда тело находится на бесконечно большом расстоянии от Земли, тогда на расстоянии r потенциальная энергия

выразится равенством , где М — масса Земли.

Для расстояний r₁=3R и r₂=2R, заданных в условиях задачи (рис. 4.5), получим два выражения потенциальной энергии:

Подставив эти выражения П₁ и П₂ в формулу (1), получим

Заметив, что , преобразуем последнее выражение к
виду

Подставив значения т, g, R в это выражение и произведя вычисления, найдем

Пример 6. Верхний конец стального стержня длиной l = 5 м с площадью поперечного сечения S = 4 см2 закреплен неподвижно, к нижнему подвешен груз массой т = 2-103 кг. Определить: 1) нор­мальное напряжение а материала стержня; 2) абсолютное х и относительное ε удлинения стержня; 3) потенциальную энергию П растянутого стержня.

Решение. 1. Нормальное напряжение материала растяну­того стержня выражается формулой σ=F/S, где F — сила, дейст­вующая вдоль оси стержня. В данном случае F равна силе тяжести mg и поэтому можем записать

Сделав вычисления, найдем

2. Абсолютное удлинение выражается формулой

где Е — модуль Юнга.

Подставив значения величин F, l, S и Е в эту формулу (значе­ние E взять из табл. 11) и произведя вычисления, получим

Относительное удлинение стержня

3. Потенциальная энергия растянутого стержня ,
где V — объем тела, равный S×l. Поэтому

Выполнив вычисления по этой формуле, получим

N= 12,1 Дж.

Пример 7. Из пружинного пистолета был произведен выстрел вертикально вверх. Определить высоту h, на которую поднимается пуля массой m = 20 г, если пружина жесткостью k = 196 Н/м была сжата перед выстрелом на х = 10 см. Массой пружины пренебречь.

Решение. Система пуля — Земля (вместе с пистолетом) яв­ляется замкнутой системой, в которой действуют консервативные силы — силы упругости и силы тяготения. Поэтому для решения задачи можно применить закон сохранения энергии в механике. Согласно этому закону, полная механическая энергия Е₁ системы в начальном состоянии (в данном случае перед выстрелом) равна полной энергии Е₂ в конечном состоянии (когда пуля поднялась на высоту h), т. е.

E₁=E₂, или T₁+П₁=T₂+П₂, (1)
где T₁ и T₂ — кинетические энергии системы в начальном и конеч-­
ном состояниях; П₁ и П₂— потенциальные энергии в тех же состоя­-
ниях.

Так как кинетические энергии пули в начальном и конечном со­стояниях равны нулю, то равенство (1) примет вид

П₁= П₂. (2)

Если потенциальную энергию в поле тяготения Земли на ее по­верхность принять равной нулю, то энергия системы в начальном состоянии равна потенциальной энергии сжатой пружины, т. е.

, а в конечном состоянии — потенциальной энергий пули на высоте Л, т. е.

Подставив приведенные выражения П1 и П2 в формулу (2), найдем

Произведя вычисления по последней формуле, получим h= 5 м.

Задачи

Силы тяготения. Гравитационное поле

4.1. Центры масс двух одинаковых однородных шаров находятся на расстоянии r = 1 м друг от друга. Масса m каждого шара равна 1 кг. Определить силу F гравитационного взаимодействия шаров.

4.2. Как велика сила F взаимного притяжения двух космических кораблей массой m = 10т каждый, если они сблизятся до расстояния r = 100 м?

4.3 Определить силу F взаимного притяжения двух соприка­сающихся железных шаров диаметром d = 20 см каждый.

4.4. На какой высоте h над поверхностью Земли напряженность gh гравитационного поля равна 1 Н/кг? Радиус R Земли считать известным.

4.5. Ракета, пущенная вертикально вверх, поднялась на высоту h= 3200 км и начала падать. Какой путь s пройдет ракета за первую секунду своего падения?

4.6. Радиус R планеты Марс равен 3,4 Мм, ее масса М = 6,4·1023 кг. Определить напряженность g гравитационного поля на поверхности Марса.

4.7. Радиус Земли в n= 3,66 раза больше радиуса Луны; средняя плотность Земли в k =1,66 раза больше средней плотности Луны. Определить ускорение свободного падения g_Л на поверхности Луны, если на поверхности Земли ускорение свободного падения g считать известным.

4.8. Радиус R малой планеты равен 250 км, средняя плотность ρ=3 г/см³. Определить ускорение свободного падения g на поверх­ности планеты.

4.9. Масса Земли в n= 81,6 раза больше массы Луны. Расстояние l между центрами масс Земли и Луны равно 60,3R (R — радиус Земли). На каком расстоянии r (в единицах R) от центра Земли на­ходится точка, в которой суммарная напряженность гравитацион­ного поля Земли и Луны равна нулю?

4.10. Искусственный спутник обращается вокруг Земли по ок­ружности на высоте h= 3,6 Мм. Определить линейную скорость v спутника. Радиус R Земли и ускорение свободного падения g на поверхности Земли считать известными.

4.11. Период Т вращения искусственного спутника Земли равен

2 ч. Считая орбиту спутника круговой, найти, на какой высоте А над поверхностью Земли движется спутник.

4.12. Стационарный искусственный спутник движется по окруж­ности в плоскости земного экватора, оставаясь все время над одним и тем же пунктом земной поверхности. Определить угловую ско­рость ω спутника и радиус R его орбиты.

4.13. Планета Нептун в k =30 раз дальше от Солнца, чем Земля. Определить период Т обращения (в годах) Нептуна вокруг Солнца.

4.14. Луна движется вокруг Земли со скоростью υ₁=1,02 км/с. Среднее расстояние l Луны от Земли равно 60,3 R (R — радиус Земли). Определить по этим данным, с какой скоростью υ₂ должен двигаться искусственный спутник, вращающийся вокруг Земли на незначительной высоте над ее поверхностью.

4.15. Зная среднюю скорость υ₁ движения Земли вокруг Солнца (30 км/с), определить, с какой средней скоростью υ₂ движется малая планета, радиус орбиты которой в n= 4 раза больше радиуса орбиты Земли.

4.16. Советская космическая ракета, ставшая первой искусствен­ной планетой, обращается вокруг Солнца по эллипсу. Наименьшее расстояние r_min ракеты от Солнца равно 0,97, наибольшее расстоя­ние r_max равно 1,31 а. е. (среднего расстояния Земли от Солнца). Определить период Т вращения (в годах) искусственной планеты.

4.17. Космическая ракета движется вокруг Солнца по орбите, почти совпадающей с орбитой Земли. При включении тормозного устройства ракета быстро теряет скорость и начинает падать на Солнце (рис. 4.6). Определить время t, в течение которого будет падать ракета.

Указание. Принять, что, падая на Солнце, ракета движется по эллипсу, большая ось которого очень мало отличается от радиуса орбиты Земли, а эксцентриситет — от единицы. Период обращения по эллипсу не зависит от эксцентриситета.

4.18. Ракета, запущенная с Земли на Марс, летит, двигаясь во­круг Солнца по эллиптической орбите (рис. 4.7). Среднее расстоя­ние r планеты Марс от Солнца равно 1,5 а. е. В течение какого вре­мени t будет лететь ракета до встречи с Марсом?

4.19. Искусственный спутник движется вокруг Земли по эллипсу с эксцентриситетом ε=0,5. Во сколько раз линейная скорость спут­ника в перигее (ближайшая к центру Земли точка орбиты спутника) больше, чем в апогее (наиболее удаленная точка орбиты)?

Указание. Применить закон сохранения момента импульса.

 

Рис. 4.6 Рис. 4.7

4.20. Комета движется вокруг Солнца по эллипсу с эксцентриси­тетом ε=0,6. Во сколько раз линейная скорость кометы в ближайшей к Солнцу точке орбиты больше, чем в наиболее удаленной?

4.21. Ближайший спутник Марса находится на расстоянии r=9,4 Мм от центра планеты и движется вокруг нее со скоростью υ=2,1 км/с. Определить массу М Марса.

4.22. Определить массу М Земли по среднему расстоянию r от центра Луны до центра Земли и периоду Т обращения Луны вокруг Земли (Т и r cчитать известными).

4.23. Один из спутников планеты Сатурн находится приблизи­тельно на таком же расстоянии r от планеты, как Луна от Земли, но период Т его обращения вокруг планеты почти в n= 10 раз мень­ше, чем у Луны. Определить отношение масс Сатурна и Земли.

4.24. Найти зависимость ускорения свободного падения g от расстояния r, отсчитанного от центра планеты, плотность ρ которой можно считать для всех точек одинаковой. Построить график зави­симости g (r). Радиус R планеты считать известным.

4.25. Тело массой m= 1 кг находится на поверхности Земли. Определить изменение ΔР силы тяжести для двух случаев: 1) при подъеме тела на высоту h= 5 км; 2) при опускании тела в шахту на глубину h= 5 км. Землю считать однородным шаром радиусом R=6,37 Мм и плотностью ρ =5,5 г/см3.

4.26. Определить работу A, которую совершат силы гравитаци­онного поля Земли, если тело массой m= 1 кг упадет на поверхность Земли: 1) с высоты h, равной радиусу Земли; 2) из бесконечности. Радиус R Земли и ускорение свободного падения g на ее поверхности считать известными.

4.27. На какую высоту h над поверхностью Земли поднимется ракета, пущенная вертикально вверх, если начальная скорость υ ракеты равна первой космической скорости?

4.28. Определить значения потенциала φ гравитационного поля на поверхностях Земли и Солнца.

4.29. Вычислить значения первой (круговой) и второй (параболи­ческой) космических скоростей вблизи поверхности Луны.

4.30. Найти первую и вторую космические скорости вблизи поверхности Солнца.

4.31. Радиус R малой планеты равен 100 км, средняя плотность ρ вещества планеты равна 3 г/см³. Определить параболическую ско­рость υ₂ у поверхности этой планеты.

4.32. Какова будет скорость v ракеты на высоте, равной радиусу Земли, если ракета пущена с Земли с начальной скоростью υ₀= 10 км/с? Сопротивление воздуха не учитывать. Радиус R Земли и ускорение свободного падения g на ее поверхности считать извест­ными.

4.33. Ракета пущена с Земли с начальной скоростью υ_о=15 км/с. К какому пределу будет стремиться скорость ракеты, если расстоя­ние ракеты от Земли бесконечно увеличивается? Сопротивление воздуха и притяжение других небесных тел, кроме Земли, не учи­тывать.

4.34. Метеорит падает на Солнце с очень большого расстояния, которое практически можно считать бесконечно большим. Начальная скорость метеорита пренебрежимо мала. Какую скорость υ будет иметь метеорит в момент, когда его расстояние от Солнца равна среднему расстоянию Земли от Солнца?

4.35. Комета огибает Солнце, двигаясь по орбите, которую мож­но считать параболической. С какой скоростью υ движется комета, когда она проходит через перигей (ближайшую к Солнцу точку своей орбиты), если расстояние r кометы от Солнца в этот момент равно 50 Гм?

4.36. На высоте h= 2,6Мм над поверхностью Земли космической ракете была сообщена скорость υ=10 км/с, направленная перпенди­кулярно линии, соединяющей центр Земли с ракетой. По какой орбите относительно Земли будет двигаться ракета? Определить вид конического сечения.