Уравнения линейной и степенной производственной функции
Линейная производственная функция
Согласно вариантным данным, используя встроенную функцию Excel «Анализ данных – Регрессия», получим следующую таблицу:
Таблица 3
Регрессионная статистика значений линейной функции
| Регрессионная статистика | ||||||||
| Множественный R | 0,997339368 | |||||||
| R-квадрат | 0,994685815 | |||||||
| Нормированный R-квадрат | 0,917353954 | |||||||
| Стандартная ошибка | 1,234384756 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 3707,606926 | 1853,803463 | 1216,641398 | 1,39673E-14 | ||||
| Остаток | 19,80817442 | 1,523705725 | ||||||
| Итого | 3727,4151 | |||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | #Н/Д | |
| K | 0,214212108 | 0,084681862 | 2,529610271 | 0,025143432 | 0,031268068 | 0,397156148 | 0,031268068 | 0,397156148 |
| L | 0,342666714 | 0,115335109 | 2,971052929 | 0,010824893 | 0,09350036 | 0,591833069 | 0,09350036 | 0,591833069 |
Из данной статистики выведем уравнение линейной функции:
Y = 0,214K + 0,343L
Степенная производственная функция
Для степенной функции проделаем аналогичные действия, но уже используя преобразованные значения из таблицы 2.
Таблица 4
| Регрессионная статистика | ||||||||
| Множественный R | 0,490895173 | |||||||
| R-квадрат | 0,240978071 | |||||||
| Нормированный R-квадрат | 0,114474416 | |||||||
| Стандартная ошибка | 0,07470474 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 0,021261836 | 0,010630918 | 1,904909953 | 0,191216753 | ||||
| Остаток | 0,066969578 | 0,005580798 | ||||||
| Итого | 0,088231414 | |||||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 1,433026057 | 1,099066333 | 1,30385766 | 0,216740004 | -0,961633768 | 3,827685882 | -0,961633768 | 3,827685882 |
| lnK | 0,020404076 | 0,297122088 | 0,068672364 | 0,946381456 | -0,626969341 | 0,667777494 | -0,626969341 | 0,667777494 |
| lnL | 0,389561315 | 0,207138046 | 1,880684509 | 0,08449766 | -0,061753717 | 0,840876347 | -0,061753717 | 0,840876347 |
Также выведем уравнение степенной функции:
Y = 1,433K0,020L0,390
Анализ полученных производственных функций
Линейная функция
1) Коэффициент множественной корреляции
R = 0,9973, т.е. связь прямая и очень тесная
2) Коэффициент детерминации
R2 = 0,995, т.е. выпуск продукции зависит от факторов «затраты основных производственных фондов» и «ресурсы трудозатрат» на 99,5%.
3) Критерий Фишера
Fтабл.(0,05;2;13) = 3,81;
Fнабл. = 1216,64.
Fнабл. > Fтабл. , т.е. уравнение в целом статистически значимо.
4) Критерий Стьюдента
tтабл. (0,05;13) = 2,16;
tb = 2,53, т.е. параметр статистически значим;
ta = 2,97, т.е. параметр статистически значим.
Степенная функция
1) Коэффициент множественной корреляции
R = 0,4909, т.е. связь прямая и умеренная
2) Коэффициент детерминации
R2 = 0,241, т.е. выпуск продукции зависит от факторов «затраты основных производственных фондов» и «ресурсы трудозатрат» на 24,1%
3) Критерий Фишера
Fтабл.(0,05;2;13) = 3,81;
Fнабл. = 1,905;
Fнабл. < Fтабл. , т.е. уравнение в целом статистически не значимо.
4) Критерий Стьюдента
tтабл. (0,05;13) = 2,16;
tb = 0,069, т.е. параметр статистически не значим;
ta = 1,881, т.е. параметр статистически не значим.
Таким образом, можно сделать вывод, что линейная функция лучше описывает зависимость между факторами «затраты основных производственных фондов», «ресурсы трудозатрат» и объемом выпуска, так как коэффициент детерминации выше.
Экономический анализ линейной производственной функции
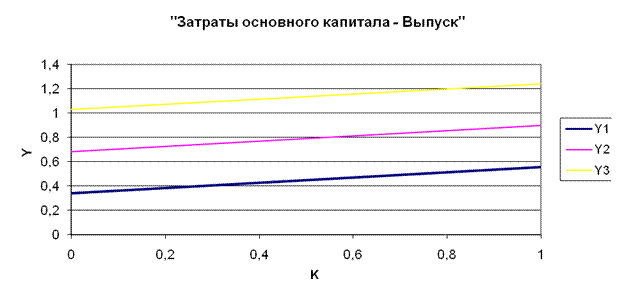
4.1. Построим графики «затраты-выпуск»
1) Y = f (K) Y = 0,214K + 0,343L
а) при L1 = 1, Y1 = 0,343 + 0,214K
Найдем точки, по которым будет проходить прямая.
| K | ||
| Y | 0,343 | 0,557 |
б) при L2 = 2, Y2 = 0,685 + 0,214K
Найдем точки, по которым будет проходить прямая.
| K | ||
| Y | 0,685 | 0,9 |
в) при L3 = 3, Y3 = 1,028 + 0,214K
Найдем точки, по которым будет проходить прямая.
| K | ||
| Y | 1,028 | 1,242 |
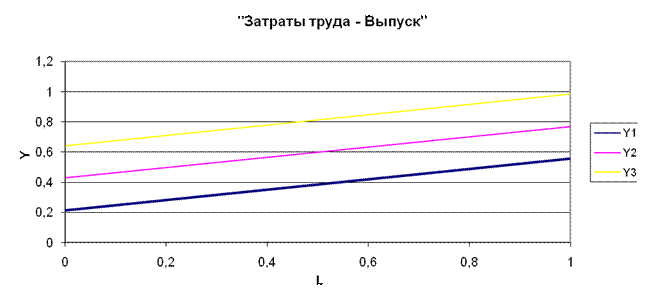
2) Y = f (L) Y = 0,214K + 0,343L
а) при K1 = 1, Y1 = 0,214 + 0,343L
Найдем точки, по которым будет проходить прямая.
| L | ||
| Y | 0,214 | 0,557 |
б) при K2 = 2, Y2 = 0,428 + 0,343L
Найдем точки, по которым будет проходить прямая.
| L | ||
| Y | 0,428 | 0,771 |
в) при K3 = 3, Y3 = 0,643 + 0,343L
Найдем точки, по которым будет проходить прямая.
| L | ||
| Y | 0,643 | 0,985 |
4.2 Рассчитаем формулы для определения:
— средней эффективности (отдачи) производственных ресурсов;
ФL = 0,343 + 0,214 
ФK = 0,214 + 0,343 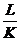
— предельной эффективности ресурсов;
VL = 0,343
VK = 0,214
4.3 Рассчитаем коэффициенты эластичности выпуска по ресурсам:
EL = 0,343 / (0,343 + 0,214);
EK = 0,214 / (0,214 + 0,343).
4.4 Построим изокванты модели
Y = 0,214K + 0,343L
а) при Y1 = 1, K1 = 4,668 - 1,600L,
| L | 2,918 | |
| K | 4,668 |
б) при Y2 = 1,5, K2 = 7,002 - 1,600L,
| L | 4,377 | |
| K | 7,002 |
в) при Y3 = 2, K3 = 9,337 - 1,600L,
| L | 5,837 | |
| K | 9,337 |
