Структурные схемы гомоморфной обработки и анализа речевых сигналов

 

Одно из основных предположений состоит в том, что речевой сигнал трактуется как сигнал на выходе линейной системы с медленно изменяющимися параметрами. Это предположение позволяет считать, что на коротких сегментах речевой сигнал можно рассматривать как сигнал на вы­ходе линейной системы с постоянными параметрами, возбуждаемой либо последовательностью импульсов, либо случайным шумом.. Поскольку сигнал возбуждения и импульсная характеристика фильтра взаимодействуют через операцию свертки, задача анализа речи может рассматриваться как задача разделения компонент, участвующих в операции свертки. Такая задача иногда называется задачей обратной свертки.

Гомоморфные относительно свертки системы. Гомоморфные относительно свертки системы удовлетворяют обобщенному принципу суперпозиции. Принцип суперпозиции для линейных систем можно представить в виде следующих соотношений

 

(1)

(2)

 

где L – линейный оператор.

Принцип суперпозиции устанавливает, что если сигнал на входе является линейной комбинацией элементарных сигналов, то и сигнал на выходе будет представлен в виде линейной комбинации соответствующих сигналов.

Прямым следствием принципа суперпозиции является тот факт, что сигнал на выходе линейной системы может быть представлен в виде дискретной свертки:

 

(3)

 

где – импульсный отклик линейной системы.

Этот принцип иллюстрируется на рис. 1, где символ «+ » на входе и выходе означает, что аддитивная комбинация сигналов на входе приво­дит к аддитивной комбинации выходных сигналов.

 

 

а) б)

 

Рис. 1. Представление линейной системы, для которой выполняется принцип суперпозиции (а)и гомоморфной относительно свертки (б)

 

Символ «* » означает свертку в дискретном времени. По аналогии с принципом суперпозиции для обычных линейных систем определим класс систем, удовлетворяющих обобщенному принципу суперпозиции, в котором сложение заменяется сверткой (легко показать, что свертка обладает такими же алгебраическими свойствами, как и сложение:

 

(4)

 

Системы, обладающие свойством (4), названы гомоморфными относительно свертки системами. Эта терминология объясняется тем, что данные преобразования оказываются гомоморфными преобразованиями линейного векторного пространства. При изображении таких систем (рис. 1, б) операцию свертки представляют в явном виде на входе и выходе системы. Гомоморфный фильтр является гомоморфной системой, обладающей тем свойством, что одна компонента (выделяемая) проходит через эту систему без изменений, а другая – устраняется. В соотношении (4), например, если – нежелательная компонента, то необходимо потребовать, чтобы выход, соответствующий , представлял собой единичный отсчет, в то время как выход, соответствующий , близко совпадал бы с .

Важным аспектом теории гомоморфных систем является то, что любая из них может быть представлена в виде каскадного соединения трех гомоморфных систем (2) для случая систем, гомоморфных относительно свертки. Первый блок преобразует компоненты на входе, представленные в виде свертки, в аддитивную сумму на выходе. Второй блок – обычная линейная система, удовлетворяющая принципам суперпозиции в соответствии с (1).

 

 

Рис. 2. Каноническая форма системы, гомоморфной относительно свертки

 

Третий блок является обратным первому, т. е. преобразует сигналы, представленные в виде суммы, в сигналы, представленные в виде свертки. Важность данного канонического представления заключается в том, что разработка гомоморфной системы сводится к разработке линейной системы. Блок, обозначаемый и называемый характеристическим блоком гомоморфной относительно свертки системы, фиксирован при каноническом представлении (рис. 2). Очевидно, что обратное преобразование также фиксировано. Характеристическая система для гомоморфной обратной свертки подчиняется обобщенному принципу суперпозиции, в котором операция на входе – свертка, а на выходе – обычное сложение. Свойства характеристической системы определяются выражением

 

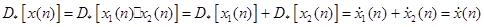(5)

 

Аналогично обратная характеристическая система удовлетворяет соотношению

 

(6)

 

Математическое описание характеристической системы определяется требованиями к выходному сигналу. Если на входе имеется сигнал свертки, то

 

(7)

и z-преобразование входного сигнала имеет вид

. (8)

 

Из (5) очевидно, что z-преобразование сигнала на выходе системы должно представлять собой сумму z-преобразований компонент. Таким образом, в частотной области характеристическая система для свертки должна обладать следующим свойством: если на входе имеется произведение компонент, то на выходе должна возникнуть их сумма. Один из подходов к синтезу такой системы представлен на рис. 3.

 

Рис. 3. Представление системы, гомоморфной относительно свертки в частотной области

 

Этот подход основан на том, что логарифм произведения равен сумме логарифмов сомножителей, т. е.

 

(9)

 

Если необходимо представлять сигналы во временной, а не в частотной области, то характеристическая система примет вид, представленный на рис. 4.

 

Рис. 4. Представление характеристической системы, гомоморфной относительно свертки

 

Аналогичное обратное преобразование показано на рис. 5.

 

Рис.5. Представление характеристической системы, обратной гомоморфной системе

 

Представление прямой и обратной характеристических систем зависит от справедливости соотношения (9). Таким образом, логарифм должен быть определен так, чтобы логарифм произвеления равнялся сумме логарифмов сомножителей. Это тривиально для действительных положительных величин. Однако в общем случае z-преобразование имеет комплексный характер и вопрос единственности логарифма комплексной случайной величины чрезвычайно важен. С точки зрения вычислений целесообразно рассмотреть случай, когда (9) справедливо на единичной окружности, т. е. для .

Для решаемых задач цифровой обработки вполне подходит определение логарифма в виде

 

(10)

 

В этом соотношении действительная часть не вызывает трудностей. Проблема единственности возникает при определении мнимой части (т.е. ), которая представляет собой фазовый угол z-преобразования, вычисленного на единичной окружности. Одним из подходов к решению проблемы единственности является предположение, что фазовый угол представляет собой непрерывную нечетную функцию. В этих условиях уравнение (9) справедливо.

С учетом возможности вычисления комплексного логарифма, удовлетворяющего (9), обратное преобразование комплексного логарифма преобразования Фурье входного сигнала, являющееся выходом характеристической системы для свертки, имеет вид

 

(11)

 

Выход характеристической системы назван «комплексным кепстром» (термин «кепстр» является в настоящее время общепринятым для обозначения обратного преобразования Фурье логарифма спектра мощности сигнала; термин «комплексный кепстр» означает, что применяется комплексный логарифм).

Термин «кепстр» используется для величины

 

(12)

 

Последовательность с(п) представляет собой четную часть комплексного кепстра : .

Таким образом, определена характеристическая система для гомоморфной свертки и каноническая форма всех гомоморфных систем относительно свертки. Все системы этого класса отличаются только линейной частью. Выбор линейной системы определяется свойствами входного сигнала. Следовательно, для правильного построения линейной системы необходимо прежде всего определить вид и структуру сигнала на выходе характеристической системы, т.е. рассмотреть свойства комплексного кепстра для типичных входных сигналов.

 

Комплексный кепстр речи

 

Модели сигналов, с одной стороны, и методы анализа во временной области – с другой, можно объединить и эффективно использовать в теории гомоморфной фильтрации речи. Вспомним, что модель речеобразования обязательно состоит из линейной системы с медленно изменяющимися во времени параметрами и сигнала возбуждения в виде последовательности импульсов или белого шума. Поэтому короткий сегмент вокализованного речевого сигнала целесообразно рассматривать как результат воздействия сигнала возбуждения в виде последовательности импульсов на линейную систему с постоянными параметрами. Аналогично короткий сегмент невокализованного сигнала можно представить как результат возбуждения линейной системы с постоянными параметрами случайным шумом.

Короткий сегмент вокализованной речи можно представить в виде

 

(13)

 

где – периодическая импульсная последовательность с периодом N_p отсчетов; – импульсная характеристика линейной системы, отражающая эффект формы источника возбуждения g(n), импульсную характеристику речевого тракта и импульсную характеристику

Короткий сегмент невокализованной речи можно представить в виде

 

(14)

 

где – сигнал возбуждения в виде случайного шума; – импульсная реакция системы, объединяющая воздействие речевого тракта и излучения.

Для случая вокализованной речи передаточная функция линейной системы имеет вид

(15)

 

Для невокализованной речи получаем

(16)

 

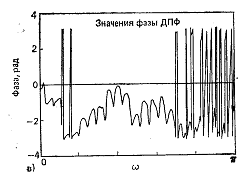
Комплексный кепстр быстро затухает с ростом п. Кроме того, отметим, что вклад в комплексный кепстр от периодического возбуждения проявится в наличии импульсов в точках, кратных периоду возбуждения. Пример анализа (рис.6) иллюстрирует основные особенности вокализованного речевого сигнала.

 

а) б)

в) г)

д) е)

Рис. 6. Гоморфный анализ вокализованный речи: а) взвешенный речевой сигнал; б) логарифм модуля кратковременного Фурье; в) значение фазы; г) «развернутая» фаза; д) комплексный кепстр; е) кепстр

 

На рис. 6,а показан сегмент вокализованного сигнала, взвешенный с окном Хемминга. На рис.6,б представлен логарифм модуля дискретного преобразования Фурье. В этой функции имеется периодическая компонента, обусловленная периодическим характером входного сигнала. На рис.6,в представлен разрывной характер главного значения фазы, а на рис. 6,г – фазовая кривая, лишенная разрывов. Результат преобразования Фурье в комплексный кепстр кривых на рис.6,б и 6,г представлен на рис.6,д.

Отметим наличие пиков в положительном и отрицательном времени и быстрое затухание компонент в области малых времен, что обусловлено совместным воздействием речевого тракта, источника возбуждения и излучением. Кепстр, являющийся обратным преобразованием Фурье логарифма амплитуды модуля спектра, показан на рис.6,е. В данном случае сохранены все основные особенности комплексного кепстра, поскольку он является четной частью комплексного кепстра.

Последовательность графиков на рис.6 показывает, как можно использовать гомоморфную фильтрацию для анализа речевого сигнала. Прежде всего отметим, что импульс в кепстре, обусловленный квазипериодическим возбуждением, оказывается отделенным от остальных компонент. Это приводит к соответствующей системе гомоморфной фильтрации речевого сигнала, представленной на рис. 7.

 

Рис. 7. Реализация системы гомоморфной фильтрации речи

 

Сегмент речевого сигнала взвешивается с некоторым окном и требуемые компоненты кепстра выделяются с использованием «окна по кепстру» . Если выбрать в соответствии ссотношением

 

(17)

 

где выбрано меньшим, чем период основного тона , то выходной сигнал аппроксимирует импульсную реакцию, определяемую (13). Этот вид фильтрации иногда называют «частотно-инвариантной линейной фильтрацией».

Если выбрать 1{п) таким образом, чтобы восстановить компоненты возбуждения, т. е.

 

(18).

 

то выходной сигнал аппроксимирует импульсную последовательность возбуждения, амплитуды которой затухают в соответствии с весами окна Хемминга, примененного при взвешивании входного сигнала.

В результате взвешенный комплексный кепстр подвергается обратному преобразованию для получения требуемых компонент.

Таким образом, с помощью гомоморфной фильтрации можно выделить ряд важных компонент речевого сигнала. Чаще сталкиваются с необходимостью оценки таких параметров, как период основного тона и частоты формант. Для этих целей кепстральный анализ весьма эффективен. Для вокализованного сегмента речи пик в кепстре возникает при задержке, соответствующей периоду основного тона. Для невокализованного сегмента такие пики в кепстре не возникают. Это свойство кепстра может быть использовано для классификации вокализованный/невокализованный и для периода основного тона на вокализованной речи.

Частоты формант также можно определить с использованием логарифма модуля передаточной функции речевого тракта, ко­торая вычисляется по кепстру с помощью кепстрального окна (17).