Силовое поле.
Силовым полем называется область, в каждой точку которой, на помещённую в неё материальную точку действует сила однозначно определённая по величине и направлению в любой момент времени.
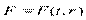
Силовое поле определяется уравнениями:
.
Силовое поле называется не стационарным, если поле зависит явно от времени; и стационарным, если не зависит от времени t явно.
Будем рассматривать только стационарные силовые поля.
Стационарное силовое поле называется потенциальным, когда существует однозначная скалярная функция 
, зависящая только от координат точки и такая, что проекция силы на декартовые оси координат равны соответствующим частным производным этой функции U:
Связь между силой и потенциальной энергией.
Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы 
, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии 
. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.
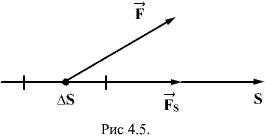
Для установления этой связи вычислим элементарную работу 
, совершаемую силами поля при малом перемещении 
тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой 
. Эта работа равна
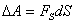
где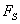 
- проекция силы на направление .
Поскольку в данном случае работа совершается за счет запаса потенциальной энергии , она равна убыли потенциальной энергии 
на отрезке оси :
Из двух последних выражений получаем
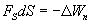
Откуда
Последнее выражение дает среднее значение 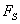на отрезке . Чтобы
получить значение 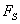в точке нужно произвести предельный переход:
Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :
Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:
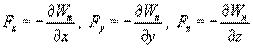
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
в математике вектор 
,
где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом 
. Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком
|
Движение в центральном поле.
Поле, в котором потенциальная энергия зависит только от расстояния r до определенной неподвижной точки, называют центральным[1].
Сила
, (2)
действующая на частицу, по абсолютной величине зависит при этом тоже только от 
и направлена в каждой точке вдоль радиус-вектора.
При движении в центральном поле сохраняется момент количества движения системы относительно центра поля. Для одной частицы это есть
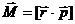. (3)
Поскольку векторы 
и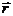 
взаимно перпендикулярны, постоянство означает, что при движении частицы ее радиус-вектор все время остается в одной плоскости – плоскости, перпендикулярной . Таким образом, траектория движения частицы в центральном поле лежит целиком в одной плоскости.