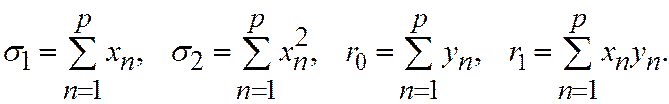Метод наименьших квадратов широко используется для обработки экспериментальных данных, точки которых измерены с заметной погрешностью 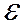 .
.
Очевидно же, что при наличии значительных ошибок эксперимента Ньютоновская интерполяция неразумна. Это хорошо видно из рис. 8.1, показывающего описание изменений радиоактивного распада в выравнивающих переменных интерполяционным многочленом Ньютона и прямой линией, найденной методом наименьших квадратов.

Итак, из рисунка 8.1 мы приходим к выводу, что здесь надо через экспериментальные точки провести прямую линию  и она, по физике, будет ближе к истине, нежели чем многочлен Ньютона. То есть, теперь наша задача найти константы
и она, по физике, будет ближе к истине, нежели чем многочлен Ньютона. То есть, теперь наша задача найти константы  и
и  .
.
Как это сделать? Рассмотрим ещё более простой пример. Предположим, что у пропорционально х, т.е. ищем формулу вида  .
.
Теперь задача сводится к определению всего лишь одного коэффициента k. При такой формуле каждый опыт дает определенное значение k, именно

где xn, yn – значения величин х, у, полученные в n -м опыте. Индекс n у величины k показывает, что это значение, соответствующее n -му опыту. Из значений kn можно образовать среднее, положив

где р – общее число опытов. Мы получаем формулу 
Отметим, что это – самый простой, но не самый лучший метод выбора величины  .
.
Поставим задачу о нахождении значения k, при котором функция у = kх наилучшим образом соответствует опытным данным, т.е. будем искать k не как среднее арифметическое, а по-другому.
За меру отклонения функции от экспериментальных данных для n -го опыта выберем величину  которое называется
которое называется  -ым уклонением. Спрашивается почему
-ым уклонением. Спрашивается почему  а не
а не  Ясно, что оба знака уклонения kхn от уn нехороши: плохо, если k таково, что уn < kхn,но также нехорошо, если k таково что уn > kхn. Если бы за меру уклонения мы взяли величину уn - kхn, а затем стали находить сумму уклонений в нескольких опытах, то мы могли бы получить весьма малую величину за счет взаимного уничтожения отдельных слагаемых большой величины, но разных знаков. Это, однако, вовсе не говорило бы о том, что взятая функция у = kх хороша. Если же за меру уклонения взять
Ясно, что оба знака уклонения kхn от уn нехороши: плохо, если k таково, что уn < kхn,но также нехорошо, если k таково что уn > kхn. Если бы за меру уклонения мы взяли величину уn - kхn, а затем стали находить сумму уклонений в нескольких опытах, то мы могли бы получить весьма малую величину за счет взаимного уничтожения отдельных слагаемых большой величины, но разных знаков. Это, однако, вовсе не говорило бы о том, что взятая функция у = kх хороша. Если же за меру уклонения взять  то такого взаимного уничтожения не произойдет, так как все величины
то такого взаимного уничтожения не произойдет, так как все величины  положительны. Отметим, что вместо
положительны. Отметим, что вместо  в принципе, можно было бы взять
в принципе, можно было бы взять  и т.д. Однако при этом дальнейшие вычисления значительно усложнились бы.
и т.д. Однако при этом дальнейшие вычисления значительно усложнились бы.
Теперь в качестве меры общей ошибки S в описании опытных данных функцией у = kх возьмем сумму квадратов уклонений для всех опытов, т.е.

Для того чтобы найти  при котором
при котором  наименьшее, решим уравнение
наименьшее, решим уравнение  Находим:
Находим:
 .
.
Откуда 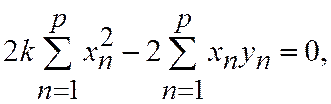 что дает
что дает

Если в каждом опыте получается точно  то из последней формулы получаем
то из последней формулы получаем 
Если для различных опытов величина  различна, то, подставляя в последнюю формулу вместо уn его значение кnxn, получим
различна, то, подставляя в последнюю формулу вместо уn его значение кnxn, получим
 (8.1)
(8.1)
Пусть среди величин k 1, k 2, … kр, полученных в различных опытах, есть наибольшая величина k max и наименьшая k min. Если заменить в правой части все kn на k max, то дробь только возрастет и мы получим

Теперь вместо k 1, k 2, …, kр подставляем k min, получим  . Таким образом, величина
. Таким образом, величина 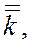 найденная из условия минимума S, удовлетворяет неравенству
найденная из условия минимума S, удовлетворяет неравенству  т.е. действительно является средней из всех значений k 1, k 2, …, kр, однако это среднее составляется по более сложному правилу, нежели
т.е. действительно является средней из всех значений k 1, k 2, …, kр, однако это среднее составляется по более сложному правилу, нежели

Итак, если мы, методом наименьших квадратов, ищем формулу вида 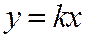 то
то  надо определять по формуле
надо определять по формуле

Теперь найдём способ подбора формулы 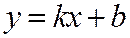 . Это тоже прямая линия, но не проходящая через начало координат.
. Это тоже прямая линия, но не проходящая через начало координат.
Если нет оснований предполагать, что у = 0 при х = 0, то наиболее простой является формула у = kх + b. В этом случае также можно применить метод наименьших квадратов. Величина S для этого случая дается формулой

Надо выбрать числа k и b так, чтобы величина S была наименьшей. Для этого поступим так. Если бы b было уже найдено, то в правой части можно было бы изменять только k, поэтому должно было бы быть

С другой стороны, если бы уже было найдено k, то должно было бы быть

Эти два условия дают нам следующую систему уравнений для определения чисел к и b

Из этой системы уравнений нетрудно найти числа k и b. С этой целью обозначим для краткости

Тогда систему можно переписать в виде
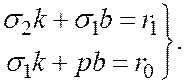
Решая ее, получим

Итак, если мы ищем формулу вида  методом наименьших квадратов, то
методом наименьших квадратов, то 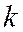 и
и  надо определять по формулам
надо определять по формулам

Где