ГРАФИЧЕСКИЙ СПОСОБ ПОДБОРА ИНТЕРПОЛЯЦИОННЫХ ФОРМУЛ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ

 

Прошлый раз мы с Вами установили, что сущность метода наименьших квадратов - это минимизация суммы квадратов всех уклонений.

Отличие метода наименьших квадратов от всех других методов состоит в том, что здесь мы сами назначаем ту или иную кривую, которая на наш взгляд наиболее правдоподобно отражает результаты опыта. При этом кривая не будет проходить по точкам, а будет проходить где-то рядом, поскольку прохождение кривой по точкам не целесообразно, т.к. точки получены в эксперименте с некоторой погрешностью.

Итак, если мы, методом наименьших квадратов, ищем формулу вида то 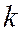надо определять по формуле

А если мы ищем формулу вида методом наименьших квадратов, то и определяются по формулам

 

Где

Оказывается экспериментальные данные можно интерполировать чисто графически. Как это делается? Вначале опытные данные наносятся на график (представляются графически на миллиметровке). Затем на глаз от руки, через полученные точки проводится наиболее правдоподобная кривая.

Очень важно при проведении кривой, кроме экспериментальных точек использовать общие соображения о том, как должна вести себя кривая при значениях аргумента, весьма близких к нулю, при больших значениях аргумента, проходит ли кривая через начало координат, пересекает ли координатные оси, касается ли их и т.д.?

Итак, пусть эта предварительная работа проделана, выбран вид формулы и нужно определить значения входящих в формулу постоянных величин.

Пусть для начала выбрана прямая линия.

Напомним, что уравнение прямой линии имеет вид у = kх + b, причем числа k и b имеют простой геометрический смысл: b есть величина отрезка, отсекаемого прямой на оси Оу, а k есть тангенс угла наклона прямой к оси Ох (рис. 9.1).

Рис. 9.1

Пусть предполагается, что величины у и х связаны линейно, т.е. у = kх + b. Нанесем экспериментальные точки на график. Наложив на график прозрачную линейку и передвигая ее, нетрудно получить такую прямую, к которой экспериментальные точки лежат ближе всего (рис. 9.2).

Рис. 9.2

Проведя эту прямую, мы определим из чертежа b и .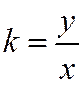

Большое преимущество графического способа связано с его наглядностью. Если экспериментальные точки ложатся на прямую за исключением отдельных выпавших точек, то эти точки наглядно выделяются и видно, какие точки следует проверить. Если экспериментальные точки в целом не лежат на прямой, то это также будет видно из графика и в этом случае зависимость между величинами х, у будет иметь более сложный вид, нежели у = kх + b.

Прямая линия занимает исключительное положение в графическом подборе формул. Никакая другая линия не может быть так просто и вместе с тем так надежно проведена по данным точкам.

Как же подобрать константы, пользуясь графиком, если формула имеет более сложный вид, чем у = kх + b?

Рассмотрим пример.

Пусть исследуется зависимость между температурой Т проволоки и силой i постоянного тока, текущего по этой проволоке. Ясно, что изменение направления тока не меняет величины Т, т.е. Т (- i) = Т (i). Поэтому зависимость Т = ai + b не годится. Будем искать формулу вида Т = ai ² + b. График такой функции Т (i) есть парабола, а провести на глаз параболу трудно. Поэтому введем новую переменную z = i ², тогда

Т = az + b,

Так что в координатах z, T искомая зависимость изображается прямой линией. При этом значение температуры b = Т ₀ при отсутствии тока можно считать известным, так что остается определить коэффициент а при i ².

Далее (по этой же задаче нагрева), при большой силе тока, когда достигаются высокие температуры, сопротивление проволоки R нельзя считать постоянным. Поэтому тепловая мощность (количество тепла, выделяющееся в единицу времени), равная 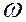= Ri ², в действительности не просто пропорциональна i ², так как меняется R. Кроме того, в уравнении теплового баланса

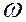= Ri ² + S (T - T ₀),

где – коэффициент теплоотдачи, а S – поверхность проволоки, при больших температурах коэффициент также непостоянен. Однако равенство температур для токов i и – i по-прежнему имеет место. Поэтому естественно добавить в формулу Т = ai² + b, которая теперь может оказаться неточной, член c i ⁴ (а не c i ³).

Итак, ищем формулу в виде

Т = ci ⁴ + ai ² + b.

Заметим, что Т = b при i = 0, так что b не отличается от температуры окружающей среды, а потому известно. Перепишем формулу так

.

Вводя новые переменные х = i ², 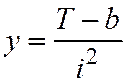, получаем у = сх + а, т.е. х и у связаны линейной зависимостью. Построив график в координатах х и у, легко определить числа а и с.

Таким образом, общая идея графического метода состоит в том, что надо ввести новые переменные так, чтобы в этих переменных интересующая нас зависимость становилась линейной.

Приведем еще несколько примеров.

Часто встречается такая зависимость между х и у, когда заведомо известно, что при х = 0 должно быть у = 0, но опытные данные на графике не ложатся на прямую. В этом случае может оказаться справедливой формула

у = ах + bх ².

Разделим все члены на х, получим

.

Положив , получим линейную зависимость z от х

z = a + bх.

Другая формула, которая может оказаться пригодной для этого случая, это у = ахⁿ.

Как определить показатель степени n? Для этого прологарифмируем обе части формулы

lgy = nlgx + lga.

Вводя новые переменные z = lgy; t = lgx получим линейную зависимость

z = lga + nt.

Вот, например, закон радиоактивного распада описывается формулой n = n ₀ e^{- t}, где n – число атомов, еще не распавшихся к моменту времени t, n ₀ – общее число атомов, - вероятность распада. Логарифмируя обе части формулы, получим

ln n = ln n ₀ - t.

Следовательно, мы получим прямую линию в координатах t, y = ln n.

При исследовании зависимости какой-либо величины х от температуры Т очень часто получается формула вида

.

Такая формула получается в тех случаях, когда дают вклад только те молекулы (или электроны), энергия которых больше величины А. Величина k – постоянная Больцмана ().

Логарифмируя, находим

Зависимость становится линейной, если рассматривать величины и . Действительно, .

Во всех рассмотренных нами примерах мы после выбора вида формулы вводили новые переменные так, чтобы зависимость между этими новыми переменными была линейной.