Введение
Динамические процессы в дискретных системах управления описываются уравнениями в конечных разностях. Удобным методом для решения разностных уравнений является операционный метод, основанный на дискретном преобразовании Лапласа. Дискретное преобразование Лапласа является обобщением обычного преобразования Лапласа на дискретные функции.
Одной из важнейших особенностей преобразования Лапласа, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.
Прямое дискретное преобразование Лапласа
Преобразование Лапласа для непрерывных оригиналов имеет вид:
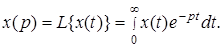 (1)
(1)
Получим формулы дискретного преобразования Лапласа. Для выхода импульсного элемента можно записать соотношение
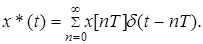 (2)
(2)
Подставив это выражение в формулу преобразования Лапласа, получим
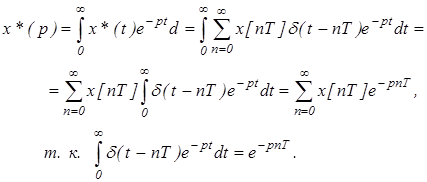 (3)
(3)
При этом получили одну из формул дискретного преобразования Лапласа, которая имеет вид:
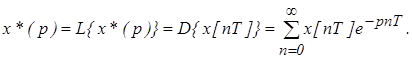 (4)
(4)
По сравнению с обычным преобразованием Лапласа для непрерывных оригиналов, интеграл заменен на сумму, а непрерывная переменная - t на дискретную - nT.
Пример 1. Определить дискретное преобразование Лапласа для единичной функции x (t) = 1 (t).
Решение: Применив формулу дискретного преобразования Лапласа, получим
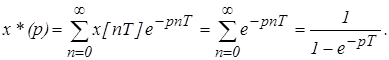
Если изображения непрерывных сигналов являются степенными уравнениями - f (pn), то изображения дискретных функций являются показательными уравнениями - f (epnT), следовательно, к ним нельзя применять аппарат теории непрерывных систем. Выполнив подстановку z = epT в формуле (4), получим
 (5)
(5)
Получили вторую формулу дискретного преобразования Лапласа, которое называется z -преобразованием. При использовании z - преобразования получаем степенные уравнения, что позволяет применять методы исследования непрерывных систем для дискретных систем с учетом некоторых особенностей.
Пример 2. Определить дискретное изображение F (z), если оригинал f (t) имеет вид (рис.1):
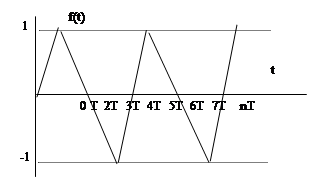 |
Рис. 1
Решение: Функцию F (z) можно представить в виде ряда
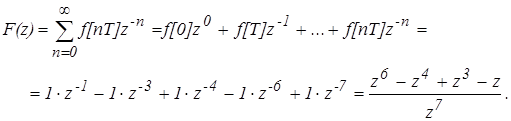
Получили дискретное преобразование исходной непрерывной функции.
Дискретное преобразование Лапласа в общем виде
Для выхода импульсного элемента можно записать соотношение
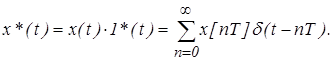 (6)
(6)
Для нахождения изображения x* (p) воспользуемся теоремой умножения в комплексной области.
Изображение произведения равно свертке изображений
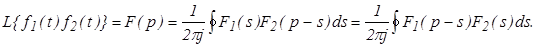
Если 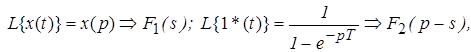 то
то
 (7)
(7)
На основании теоремы Коши о вычетах этот интеграл можно определить как сумму вычетов по полюсам подынтегральной функции.
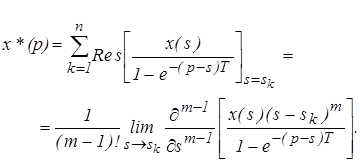 (8)
(8)
Это третья формула прямого дискретного преобразования Лапласа.
Пример 3. Определить дискретное преобразование Лапласа для еди-ничной функции.
Решение: Функции x (t) = 1 (t) соответствует изображение 
Записываем характеристическое уравнение и определяем значения полюсов, их количество и кратность. s = 0, s1 = 0, n = 1, m = 1.
Находим дискретное изображение, используя теорему Коши о вычетах по полюсам подынтегральной функции

Пример 4. Определить дискретное преобразование Лапласа для линейнорастушей функции x (t) = t.
Решение: Функции x (t) = t соответствует изображение 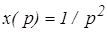 .
.
Записываем характеристическое уравнение и определяем значения полюсов, их количество и кратность. s2 = 0, s1 = 0, n = 1, m =
Находим дискретное изображение, используя теорему Коши о вычетах по полюсам подынтегральной функции
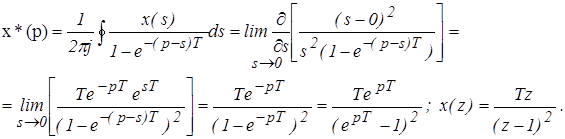
Пример 5. Определить дискретное преобразование Лапласа для экспоненциальной функции x (t) = e-at.
Решение: Функции x (t) = e-at соответствует изображение
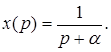
Записываем характеристическое уравнение и определяем значения полюсов, их количество и кратность. s+a = 0, s1 = - a, n = 1, m = 1.
Находим дискретное изображение, используя теорему Коши о вычетах по полюсам подынтегральной функции
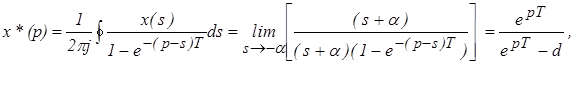
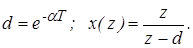


Для нахождения дискретных изображений можно использовать любую из рассмотренных выше форм дискретного преобразования Лапласа. Краткая таблица z -преобразований приведена в Приложении 3.