Метод ломаных
Это простейший численный метод, он называется еще методом Эйлера. В практике вычислений он употребляется очень редко из-за невысокой точности. Но на его примере удобно пояснить способы построения и исследования численных методов.
Рассмотрим задачу Коши  и выберем на отрезке
и выберем на отрезке  некоторую сетку
некоторую сетку  значений аргумента так, чтобы выполнялись соотношения
значений аргумента так, чтобы выполнялись соотношения  (сетка может быть неравномерной). Разлагая решение u (х) по формуле Тейлора на интервале сетки
(сетка может быть неравномерной). Разлагая решение u (х) по формуле Тейлора на интервале сетки  и обозначая u (xn) = un, получим
и обозначая u (xn) = un, получим  (19.3)
(19.3)
Стоящие в правой части производные можно найти, дифференцируя уравнение  требуемое число раз
требуемое число раз
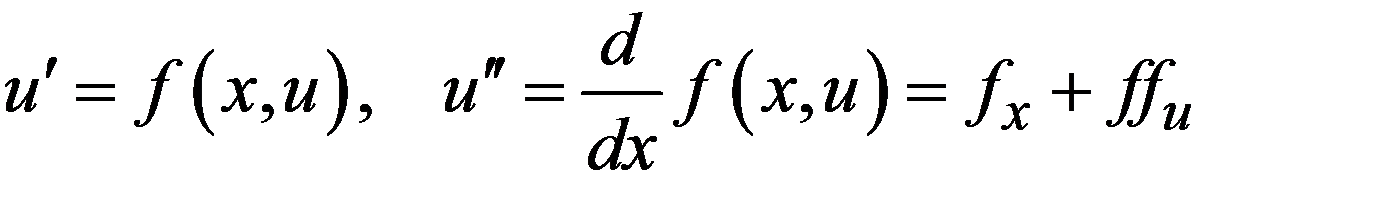 (19.4)
(19.4)
и т.д. В принципе, если f (x, u) имеет q -е непрерывные производные по совокупности аргументов, то в разложении в ряд Тейлора можно удержать члены вплоть до О (hq +1). Однако использовать для расчетов формулу Тейлора с большим числом членов невыгодно. В простейшем случае, ограничиваясь только первым членом разложения, получим схему ломаных (она же схема Эйлера)
 (19.5)
(19.5)
Поскольку при такой замене можно найти только приближенные значения искомой функции в узлах, то будем обозначать эти значения через yn в отличие от точных значений un = u (xn). Для численного расчета по схеме ломаных достаточно задать начальное значение  . Затем по итерационной формуле (19.5) последовательно вычисляются величины у 1, у 2, …, уN.
. Затем по итерационной формуле (19.5) последовательно вычисляются величины у 1, у 2, …, уN.
Геометрическая интерпретация этой схемы дана на рис. 19.1, где изображено поле интегральных кривых. Использование только первого члена формулы Тейлора означает движение не по интегральной кривой, а по касательной к ней. На каждом шаге мы заново находим касательную; следовательно, траектория движения будет ломаной линией.
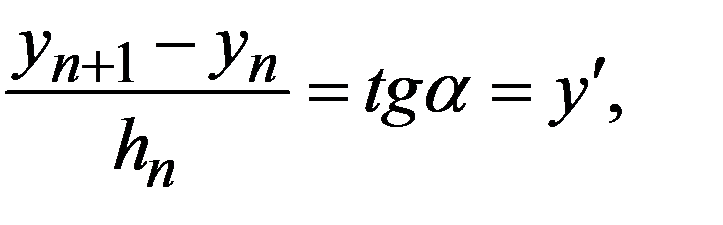 но
но 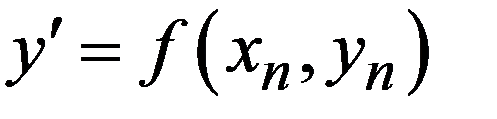 . Отсюда
. Отсюда 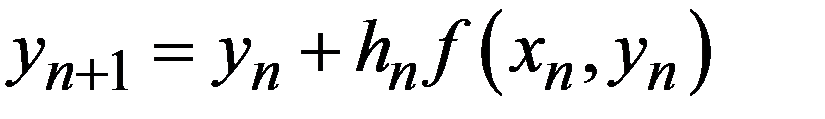 .
.
Исследуем сходимость метода ломаных, предполагая правую часть f (x, u) непрерывной и ограниченной вместе со своими первыми производными:  . Отсюда следует, что
. Отсюда следует, что  .
.
Рассмотрим погрешность приближенного решения 
Вычитая (19.3) из (19.5), получим соотношение, связывающее погрешности в соседних узлах сетки



(члены более высокого порядка малости здесь
опущены). Последовательно применяя рекуррентное соотношение (19.6), выразим погрешность на произвольном шаге через погрешность начальных данных. Поскольку, как видно из формулы (19.6)  , имеем
, имеем
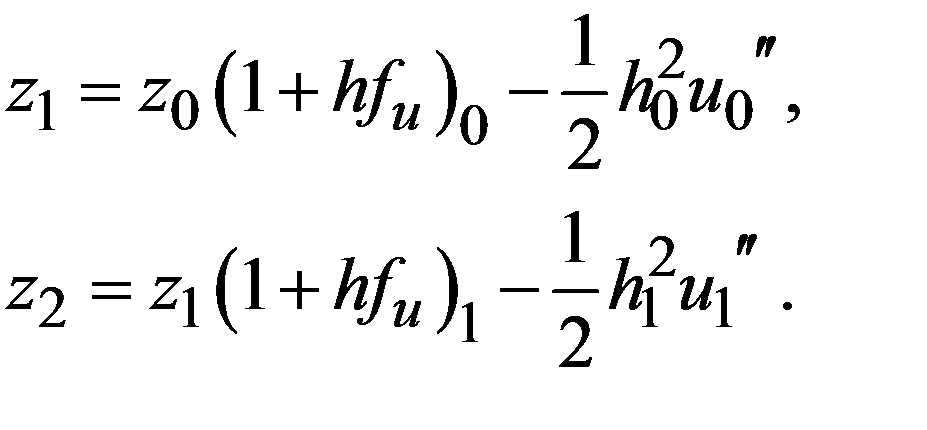
Отсюда 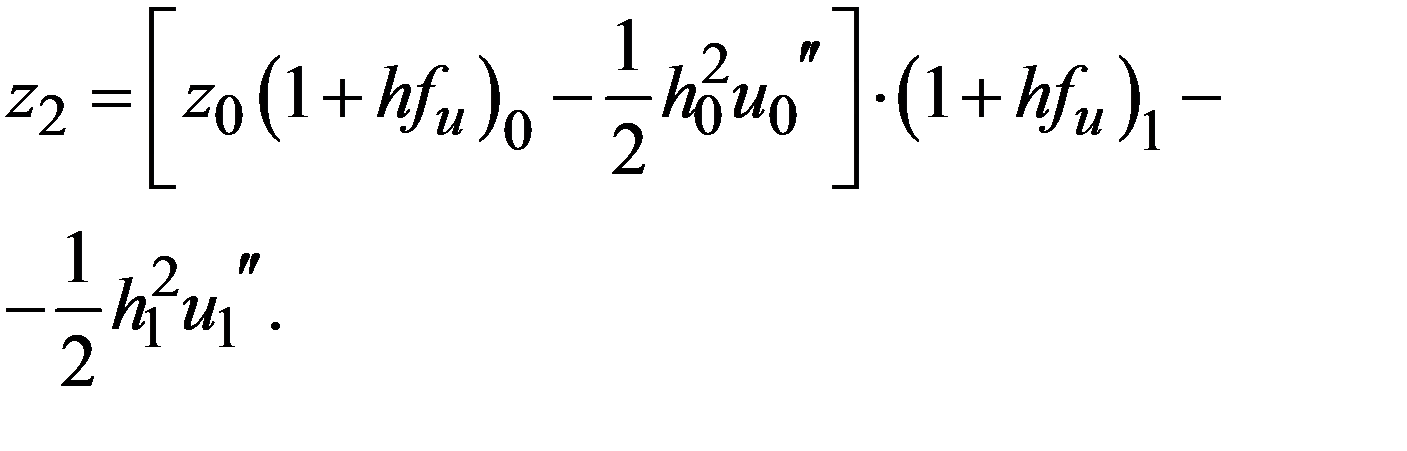
Раскрываем квадратные скобки

Отсюда видно, что для m – ного шага формула погрешности будет выглядеть следующим образом
 (19.7)
(19.7)
Отсюда нетрудно дать асимптотическую оценку погрешности. Заметим, что при малых шагах сетки справедлива формула  . Действительно, разложим функцию
. Действительно, разложим функцию  в ряд Тейлора по степеням
в ряд Тейлора по степеням  в окрестности точки
в окрестности точки 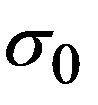 = 0
= 0
 .
.
Возьмем в качестве  функцию ех и разложим ее в ряд Тейлора в окрестности точки х 0 = 0
функцию ех и разложим ее в ряд Тейлора в окрестности точки х 0 = 0
 , т.е. при малых х:
, т.е. при малых х:  .
.
Используя это соотношение при малых шагах сетки h, получаем

причем в качестве верхнего предела интеграла можно взять хт, ибо ошибка при этом остается в пределах общей точности преобразований. Аналогично преобразуя второй член (19.7) получим
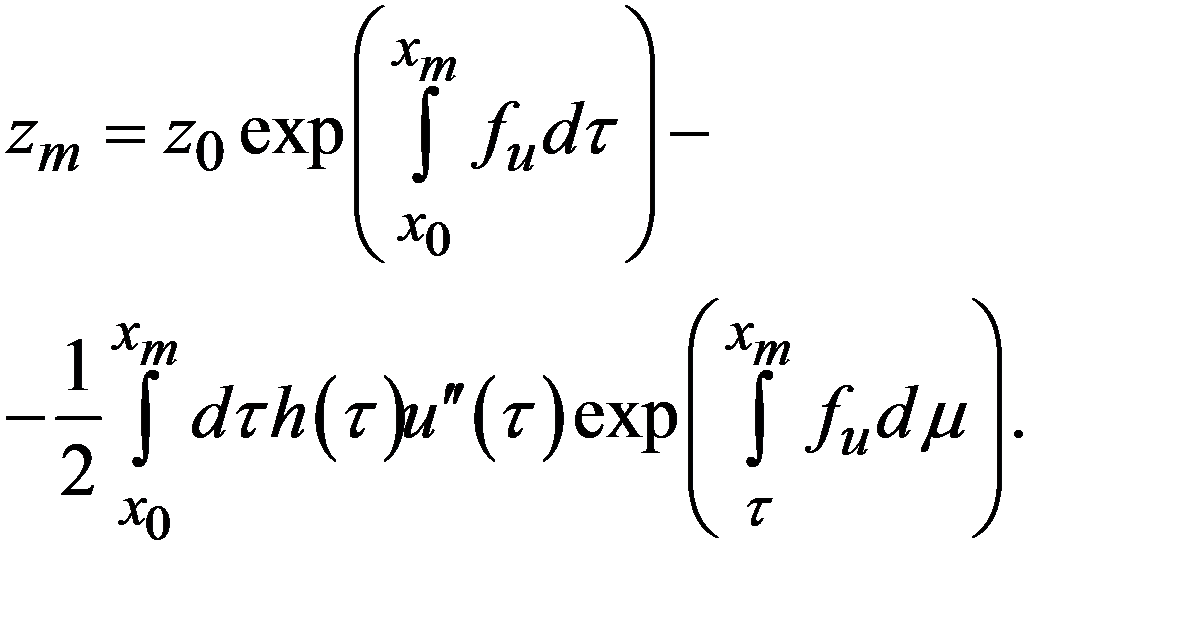 (19.8)
(19.8)
Здесь h (x) – непрерывная функция, дающая в каждом узле хn величину шага hn; в качестве такой функции можно выбрать линейный сплайн.
Рассмотрим структуру погрешности (19.8). Первое слагаемое справа связано с погрешностью начального значения z 0 = y 0 – u 0, которая умножается на ограниченную (благодаря ограниченности производных) величину. Начальное значение можно задать точно и считать, что z 0 = 0. Остановимся на втором слагаемом. Оно обусловлено тем членом формулы Тейлора (19.3), который был отброшен при выводе схемы ломаных (19.5). Оценим это слагаемое сверху; заменяя все функции под интегралами их модулями и вынося max h (x) за знак интеграла, получим 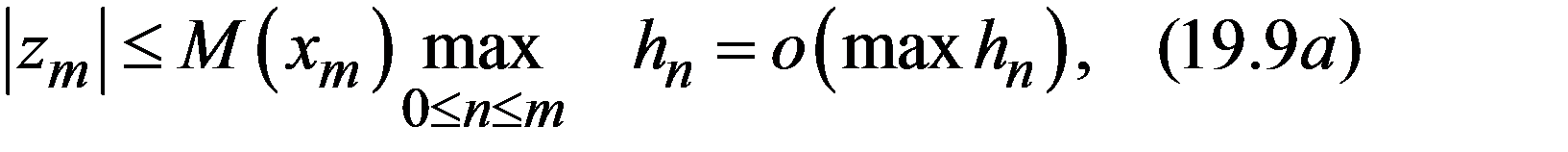 где
где 
Таким образом, при  приближенное решение сходится к точному равномерно (на ограниченном отрезке
приближенное решение сходится к точному равномерно (на ограниченном отрезке  ) с первым порядком точности.
) с первым порядком точности.
Замечание 1. Оценка погрешности (19.9) является мажорантной. Со знакопеременными производными эта оценка может быть сильно завышена по сравнению с асимптотической оценкой (19.8).
Замечание 2. Экспоненциальный член в оценке (19.9) характеризует расхождение интегральных кривых (см. рис. 19.1); если он очень велик, то исходная задача Коши плохо обусловлена.
Пример. Проинтегрируем по схеме Эйлера задачу Коши для уравнения

В таблице 19.1 даны численные решения у (х), полученные на сетках с шагами 
Эти цифры получены таким образом
 т.е.
т.е.  , у 0 =0.
, у 0 =0.
При h = 1 имеем: у 1 = 0 + 1 (02 + 02) = 0.
При h = 0,5 имеем: у 1 = 0 + 0,5(02 + 02) = 0,
у 2 =0 + 0,5((0,5)2 + 02) = 0,125.
При h = 0,25: у 1 = 0 + 0,25(02 + 02) = 0,
у 2 = 0 + 0,25((0,25)2 + 02) = 0,016,
у 3 = 0,016 + 0,25((0,5)2 +(0,016)2) = 0,078,
у 4 = 0,078 + 0,25((0,75)2 +(0,078)2) = 0,220.
Таким образом, таблица 19.1 заполняется так
Таблица 19.1
| xn | yn | u (х)-точное решение | ||
| h = 1 | h = 0,5 | h = 0,25 | ||
| 0,25 0,5 0,75 1,0 | - - - | - 0,125 | 0,016 0,078 0,220 | 0,005 0,042 0,143 0,350 |
В таблице 19.1 приведено также точное решение u (х), вычисленное методом Пикара. Видно, что схема Эйлера для получения удовлетворительной точности требует гораздо более малого шага, чем использованный здесь.